数学之旅视频 — 王维克 PPT-数学之旅 《数学之旅：数学的抽象与心智的荣耀》
数学之旅——慕课清晰版
参考笔记：1 ，2，3-ppt
图床：Calculus-zaluan-img/
关于大学教育的思考 (杨孝平) — 视频
数学的思维方式 (丘维声)— 视频
数学的意义 (席南华)— 视频 文字版
认识对称 (席南华) —— 视频
如何认识微积分方法与原理？
数学教育
- 其实学数学的最高境界就是头脑中有一个picture，然后能清晰的熟悉各种脉络，如果套套公式，纠缠于繁枝细节估计不会有什么作为的！
- 做自觉的数学人，将专业知识内化为认识、看待、对话世界的逻辑与思维方式。
- 教学过程其实是一种与先哲们心的交流，欣赏大师们的思想应该比欣赏自己的研究更有韵味，在这一尺度上看待自己的研究就会淡然很多。
- 当一个好老师其实很容易，只要真切记得自己当学生时的“痛”，并有好的办法减轻学生在学习中的“痛”。
- 我个人在数学的学习中一个特别深刻的感受是学任何东西都要琢磨它究竟是什么，并把它变成可触可摸的东西。这些可触可摸的东西我将其称为"感觉"，我们教学生就是要尽可能多地教给学生这些"感觉"，特别是抽象的数学。
- 常识是十八岁之前在头脑中所铺下的偏见层。(爱因斯坦) (整数和有理数一样多、拓扑学等等)
- “Young man, in mathematics you don’t understand things. You just get used to them.” said John Von Neumann (约翰·冯·诺伊曼)
- 只有当你致力于自我教育的时候，你才能教育别人。(乌申斯基，俄国教育家)
- 教育是一个逐步发现自己无知的过程。(杜兰特，美国作家、历史学家和哲学家)
- 数学艰难的徘徊在现实和非现实之间，数学的意义不在于形式的抽象中，也不存在于具体的实物中。数学是非现实的现实性。数学连接了心灵感知的抽象世界和完全没有生命的真实的物质世界。(《什么是数学》)
- 自然这本书是由数学来写的。(伽利略)
- 数学是科学的大门和钥匙。(Roger Bacon)
- 数学处于人类智能的中心领域。(约翰·冯·诺伊曼)
- 数学是整理出宇宙的程序。
- 对自然界的深刻的研究是数学最富饶的源泉。(傅里叶)
- 只要代数同几何分道扬镳，它们的进展就缓慢，它们的运用就狭窄，但是，当这两门学科结成伴侣的时候，就相互吸取对方的新鲜活力，便迅速地趋于完善。(拉格朗日)
- 数学的本质在于它的自由。(康托尔)
- 美是首要的试金石：丑㥛的数学不可能永存。(哈代)
数学学习
- 数学发展的前景一般来讲是：
- 从低维到高维；从线性到非线性；
- 从局部到整体；从交换到非交换；
- 从正规到奇异；从稳定到分叉混沌。
- 非线性的问题可以通过线性化来解决和理解；
- pde化成ode。
- 线性化的思想，齐次的思想，降阶的思想，局部化的思想。
- 既要注重系统知识，也要讲清楚来龙去脉，这样才能有整体的理解。比如微积分的来源有四五个motivation，说明微积分其实也是应运而生，不是一下子石头里蹦出来。
- 老师要了解数学史、科学史，要学一些现代的科技或者开展一些科学研究。
- 加强直观性和应用性的教学。直观教学是教学的一条金科玉律，只要有可能，应该用感性去接受一些东西。
- 学科方向之间是相互依赖，相互渗透，相互促进的。
- 函数的连续性、导数、积分都应该有中值定理的思想在里面，相互之间的关系区别应该交给学生。
数学教育的作用：
(1) 灌输数学知识；
(2) 提高数学的素养；(抽象思维能力，逻辑思维能力，用最简单的方式描述一个问题)；
(3) 培养应用数学的能力。(数值模拟，仿真等)
数学学习的目的：学习数学的目的是获得基础知识，学习思维方式，直到把握问题的全局，了解知识整体的框架，掌握基本的思路。
教育的本质属性：教育实际上是一种影响，是一种积极的影响，一种对人类认识和改造客观事件及自身的积极的影响。
教育的最终目的：达到教是为了不教，即教会其自我反思，自我管理的生存和发展的能力。
数学—与“造物主”对话的语言：
(1) 冥冥之中的宇宙深处伟大设计图的语言；
(2) 宇宙的伟大设计师像是一位数学家。
(3) 物理学告诉我们世界是什么样，数学告诉我们世界只能是什么样！
现代物理学的两大支柱：
(1) 爱因斯坦的相对论；
(2) 量子力学。
两个领域交界的地方还是有些悖论或者不协调的地方，这个地方就需要一种思想来协调。
《宇宙的琴弦》——数学认识世界的又一伟大尝试。对宇宙的最深刻认识将揭示一个最大的宇宙奇迹，那就是，它所依赖的基本原理是那么简单而有力。爱因斯坦渴望以前所未有的清晰来表现宇宙的活动，让每一个人都敬畏它那美貌动人的旋律。
《宇宙的琴弦》的基本思想：物质由原子组成，原子由夸克和电子组成。根据弦理论，这些粒子实际上是由闭合振动的弦构成。
《宇宙的琴弦》的要点：
(1) 一根闭合的弦的不同振动模式产生不同的质量和力荷，生成了不同的基本粒子；
(2) 闭合的弦的尺度大约是原子核的一千亿亿分之一；
(3) 以弦代替粒子可以解决相对论和量子力学之间的矛盾；
(4) 宇宙是11维的(除通常的3维空间外，还有6个转缩的空间维、1个“丢失”的空间维和1个时间维)；
(5) 多余维度的几何决定着我们在寻常三维展开空间里观察到的那些粒子的基本物理属性，如质量，电荷等；
(6) 转缩的空间可以用卡-丘(Calabi-Yau)空间描述。
弦理论是21世纪物理学偶然落到20世纪的一个部分。—E. Witten
- 数学—用理性的手指去触摸天上的星辰：
(1) 理性探索，思索本源，“算出”未知(比如发现天王星，然后计算得知周围还有一颗行星，即为后来被观察到的冥王星，即笔尖上发现的行星)；
(2) 用理性的思维达到超出人类感官及所及的宇宙的根本，和任何工具都不可达到的领地。 - 理解世界和改造世界。
- 数学—科学研究最重要的工具：
(1) 在每门具体的自然科学中，有多少数学存在，就有多少严格的科学(康德)；
(2) 科学研究的基本语言(一般性—抽象)； - 早起数学更多和哲学结盟：(芝诺、阿基米德、笛卡尔)；
- 牛顿时代及以后，数学和物理学是最好的盟友；
- 在20世纪，对科学起了里程碑作用的伟大发现，都与数学有密不可分的联系(相对论、量子力学)；
- 在21世纪，数学已深入到化学、生命科学和社会科学。
在思想上做一次轻松的数学之旅：
(1) 揭示数学思想形成的过程和历史；
(2) 理解数学抽象的必要性和魅力；
(3) 体会数学所表现出的人类心智的荣耀；
(4) 帮助学生克服数学学习的畏难情绪；
(5) 潜移默化地培养数学抽象的能力。
问题的提出：
(1) 数学学习的两类困难——抽象！
(2) 很多问题的解决本质上依赖于抽象！
(3) 一个目标，一堆数据，一些要求？
课程目的：
(1) 抽象是数学的正能量；
(2) 抽象是数学的优势，是长处，是武器；
(3) 培养出这个数学抽象的能力。
数学思维的特点：
(1) 第一层次：精确——简洁干净，没有歧义；
(2) 第二层次：严密——逻辑清晰，避免混乱；
(3) 第三层次：抽象——去伪存真，揭示本质。
数学抽象：
(1) 数学抽象就是解释本质；
(2) 数学抽象(概念、模型)是理解世界的最好武器；
(3) 数学抽象能力是数学学习的最重要的目的。
(4) 归纳提升，从个别到一般。
我们为什么要学高等代数?
数学是人类对事物的抽象结构与模式进行严格描述的一种通用手段。大体说来，数学中研究“数”的部分属于代数学的范畴；研究“形”的部分属于几何学的范畴；沟通“形” 与“数”且涉及极限运算的部分属于分析学的范畴。这三大类数学构成了整个数学的本体与核心。在这一核心的周围，由于数学通过“数” 与“形” 这两个概念与其它科学互相渗透，出现了许多边缘学科和交叉学科。
初等代数中"数"就是通常的数，不关心实数和复数领域之外的代数结构。近代数学："数"以是更广泛的数学对象，例如，多项式、向量、矩阵、变换等。初等代数进一步向两个方面发展，一方面，研究未知数更多的一次方程组(即线性方程组)；另一方面，研究未知数次数更高的高次方程。这时候，代数学已由初等代数向着高等代数的方向发展了，相应地形成了"线性代数"与"多项式理论"两大板块。事实上，现在大学里开设的高等代数课程的内容一般由这两大板块组成。
线性代数中讨论的线性空间基本上都是有限维的，随着微积分的建立以及后来泛函分析这门学科的需要，线性空间被推广至无限维，从而产生了像希尔伯特空间和巴拿赫空间等研究领域。
线性空间：一个非空集合一个域，两种运算(一内一外，加法是内运算，数乘是外运算)满足八条运算法则；线性性质\(L(a f+b g)=a L(f)+b L(g)\)，其中\(L\)是一个线性算子。积分是一个极限，微分也是一个极限，极限有线性性，所以积分/微分也有线性性。
哥尼斯堡七桥问题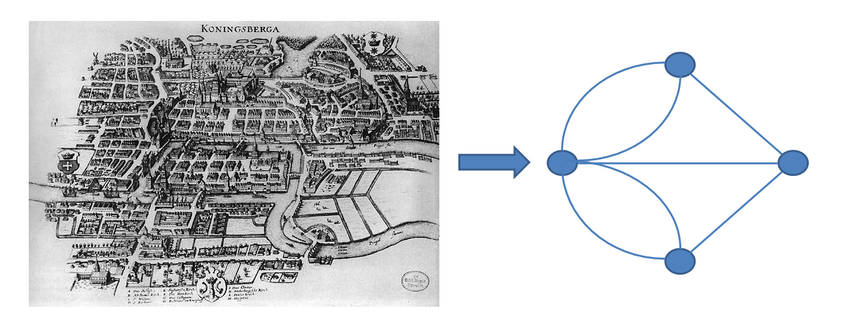
左边的实际问题抽象为右边的图，变成一笔画问题。
欧拉通过对七桥问题的研究，不仅圆满地回答了问题，而且得到并证明了更为广泛的“欧拉定理”。在解答问题的同时，开创了数学的一个新的分支—图论与几何拓扑(拓扑几何学，要害在于“连接”，圆和椭圆一样)。
- 把七桥问题转化成判断连通图是否能一笔画的问题。他不仅解决了此问题，且给出了连通图可以一笔画的充要条件是它们是连通的，且奇顶点(通过此点弧的条数是奇数)的个数为0或2；
- 一般的，有几对奇顶点，就需要几笔画完；
- 七桥问题是无解的，需要两次走完。
六人集会问题：在任意六个人的集会上，或者有三个人以前彼此认识，或者有三人以前彼此不认识。这一问题是组合学拉姆塞定理的一个特例。
圣塔菲研究所的咖啡馆：在一个咖啡馆里，顾客超过90%和低于40%就不适宜去，如果建立一个数学模型根据前几天的顾客到的情况判断今天是否应该去。
非完全理性的经济学：信息不完全，判断非完全理性。
参考：
(1) 从七桥问题开始：全面介绍图论及其应用
(2) 老师上课推荐的两本书：《别闹了，费曼先生》，《你干吗在乎别人怎么想？：充满好奇心的费曼》
(3) 郝柏林院士(个人网站)是圣菲研究所的特聘教授，他还写过一篇文章《圣菲研究所与复杂性研究》,他的文章《复杂性的刻画与“复杂性科学”》也值得学习。
(4) More is different的作者，凝聚态物理大牛P.W. Anderson也是圣塔菲研究所的创始人。
微积分
回忆小学老师教的圆的面积的计算由来，类似切西瓜。实际上面积的定义本身是在积分学完成的。曲边形面积的定义实际上要通过黎曼积分来定义。
第一阶段：穷竭法和割圆术
古希腊穷竭法：穷竭原理，给定两个不等的量，从较大的一个减去它自己的一半以上的部分，再从所余部分减去其自己的一半以上。这样，经过多次充分多次减除，可以使剩余部分小于所给的较小的量。用现代语言描述是：任意给定两个正的量\(b<a\)，从\(a\)减去\(\lambda a\)，其中\(\lambda>1 / 2\)，则必可以找到一个整数\(n\)，使得：$$(1-\lambda)^{n} a<b$$欧多克索斯利用穷竭法和反证法绕过了障碍，证明了圆的面积与其直径的平方成正比(见欧几里得《几何原本》，此书对西方思维方式的影响很大。)，即\(a(r)=A r^{2}\)，其中\(A\)是一个常数，具体不知道。
- 阿基米德用割圆术，即圆内接正多(96)边形，计算出\( \pi\)约为3.14；
- 刘徽用割圆术，即圆内接正多(192)边形，计算出\( \pi\)约为3.1416；
- 祖冲之用“缀术”(方法失传)计算出\( \pi\)约为3.1415926；
割圆术的思想：一是怎么用已知的、可求的来逼近未知的、要求的；二是用有限来逼近无穷(圆可以看作正无穷多边形)．
参考资料：《从刘徽割圆谈起》(龚昇)—— 《数学小丛书》
- 欧多克索斯的穷竭法可以严格证明已知的命题，但不能发现新的成果(例如知道面积与其直径的平方成正比，但不知道圆周率)；
- 阿基米德应用穷竭法到了出神入化的境界，他先用“平衡法”求得面积。再用“穷竭法”加以证明。把演绎数学的严格证明和创造技巧相结合：解决了许多问题；
- 除了圆周率的估计以外，还有如椭圆的面积公式、球的体积和外切的圆柱体积的关系(这可能是他在应用穷竭法得到的最辉煌的成就)。
阿基米德的羊皮书
阿基米德巧用杠杆原理称出球的体积公式，左下图分别是一个高和底面半径均为2r的圆锥，一个半径为2r的球，以及高和底面半径均为2r的圆柱。右下图就是杠杆，左侧放圆锥体和球，右侧放圆柱体。所有物体的密度都相同。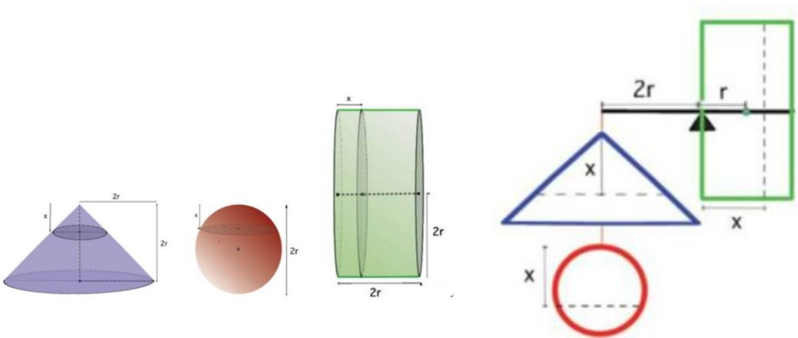
杠杆两侧分别取微小的薄片，即沿着图中的虚线切割，左侧得到两个圆片，右侧得到一个圆片。右侧圆片的的体积为\(4 \pi r^{2} d x\)，对应的到作用点的距离为\(x\)；左侧的为\(\pi[r^{2}-(x-r)^{2}] d x+\pi x^{2} d x\)，对应的到作用点的距离为\( r\)。根据力乘以力臂，通过前面的微元计算，很容易知道对于任意\(x\)属于\(0\)到\(2r\)之间的数，两侧微元的薄片都能满足力矩平衡，于是宏观整体上也能满足。在计算球的体积公式之前，阿基米德已经知道了圆柱和圆锥的计算公式，所以马上就可以通过构建三个物体的杠杆平衡公式计算出球的体积公式。
【祖暅原理】：是指所有等高处横截面积相等的两个同高立体，其体积也必然相等的定理("缘幂势既同，则积不容异")。祖冲之两父子采用这一原理，求出了牟合方盖的体积(有点麻烦)，进而算出球体积。在欧洲17世纪意大利数学家卡瓦列里亦发现相同定理，所以西方文献一般称该原理为卡瓦列里原理。
【卡瓦列里原理】：
二维情况：假设平面中的两个区域包含在该平面中的两条平行线之间。如果平行于这两条线的每条线在相等长度的线段中与两个区域相交，则这两个区域具有相等的面积。
三维情况：假设三个空间（实体）中的两个区域包含在两个平行平面之间。如果平行于这两个平面的每个平面在相等面积的横截面上与两个区域相交，则这两个区域具有相等的体积。
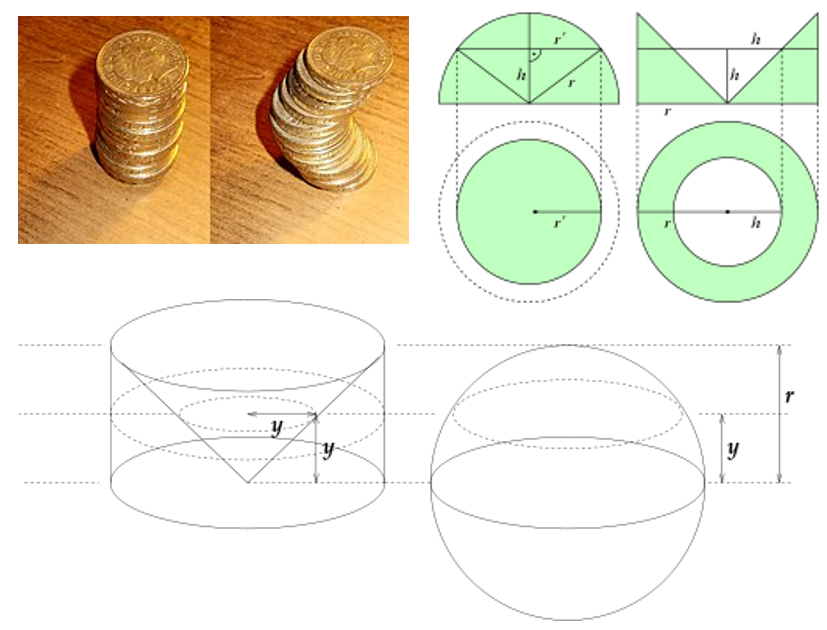(1) Two stacks of British coins with the same volume, illustrating Cavalieri's principle in three dimensions.
(2) 计算的前提是知道圆锥的体积公式还有圆柱的体积公式，上图的思想是半球的体积，等同于外切圆柱体掏空一个圆锥体。利用勾股定理，很容易知道同等高度上球的圆片面积等于圆环的面积(上图左下侧图横切)。
值得一提的是，圆或者球的面积/体积公式求导正好是它的周长或者表面积公式，因为圆面积的变化必须通过周长来变化(增加一个薄的“甜甜圈”)，球的体积变化需要通过表面积来变化(增加一个个薄的球壳层)。这个例子是为了说明我们要善于联想，将导数与“边际”联系起来。另外，在经济学领域，许多经济量，比如效用、报酬、成本、效益、净利等，都可以冠以边际两字，以表征这些经济量的变化。由于人经济行为的有限性，边际(差异、变化)的概念比总量更具有经济意涵，因此许多经济学的定律，都以边际的观念来书写。
参考资料：
(1) 数学家阿基米德的羊皮书是如何重见天日的？李永乐老师讲球的体积
(2) 价值200万美元的阿基米德数学论文长什么样？
(3) 中国古代数学家刘徽祖冲之如何算球的体积？李永乐老师讲祖暅原理
第二阶段: 牛顿和莱布尼兹的微积分
- 天文学、力学有大的发展(伽利略的天文发现和望远镜的光学研究；开普勒行星运动的三大定律;
- 刺激微分学发展的科学问题不断涌现（非匀速运动的瞬间变化率问题、光学透镜曲面的法线和切线)；
- 行星轨道计算等问题重新激发了对积分学的强烈兴趣。
- 这一阶段的特点是：找到积分的一般计算办法(微分学，微分与积分的关系)。
函数空间
常规的空间
度量空间—距离
1. 问题的提出—什么是数学的空间和距离：
(1) 研究工作的对象和遵循的规则；
(2) 元素和结构 (线性结构：加法和数乘；拓扑结构：距离、范数、开集)；
(3) 是很多工程学甚至是社会科学的语言。
围棋：其实就是一个空间，有棋子(就是元素)，也有规制(也就是规则，怎么下，怎么才算赢)，抽象出来可以看作是一个空间。
在微积分里可以定义极限和连续，依赖于“距离”。$$ \forall \varepsilon>0, \exists \delta>0,\left|x-x_0\right|<\delta \Rightarrow\left|f(x)-f\left(x_0\right)\right|<\varepsilon $$这里\(\left|x-x_{0}\right|\)是定义域里的“距离”，\(\left|f(x)-f\left(x_{0}\right)\right|\)是值域里的“距离”。
距离是一个看似很简单，实际上很复杂的一个概念。航海时，以大圆来测量距离；地球仪上不能画直线。故宫两条边上点的距离，折线意义上的距离。
(1) 两点之间的距离；
(2) 两个函数之间的距离；
(3) 两个人之间的距离(重心、鼻尖)。
2.距离、范数(向量的距离)-从具体到抽象
- 两个人的默契程度？
- 两个人的经历相似度？
- 两个人的爱好、问题看法的一致性？
- ......
以“苹果”为例
- 苹果：(1) 落叶乔木，叶子椭圆形，花白色带有红晕，果实圆形，味甜或略酸。(2) 这种植物的果实。
- 水果(属性)：可以吃的含水分较多的植物果实的统称，如苹果、梨子、桃。天下就没有水果，水果本身是一个抽象的东西，抽象的东西要用【属性】来描述。
- 热带水果：内涵多了，外延少了。
\(x=(x_{1}, \cdots, x_{n})\)到\(y=(y_{1}, \cdots, x_{n})\)的距离：
(1) 情形1 (两向量(点)之间的欧几里得距离)$$d_{1}(x, y)=\sqrt{\left(x_{1}-y_{1}\right)^{2}+\cdots+\left(x_{n}-y_{n}\right)^{2}}$$(2) 情形2 (最大分量差，专业的说法是切比雪夫距离)$$d_{2}(x, y)=\max \left\{\left|x_{1}-y_{1}\right|, \cdots,\left|x_{n}-y_{n}\right|\right\}$$(3) 情形3 (城区距离，专业的说法是曼哈顿距离/计程车几何)$$d_{3}(x, y)=\left|x_{1}-y_{1}\right|+\cdots+\left|x_{n}-y_{n}\right|$$下图是9 Distance Measures in Data Science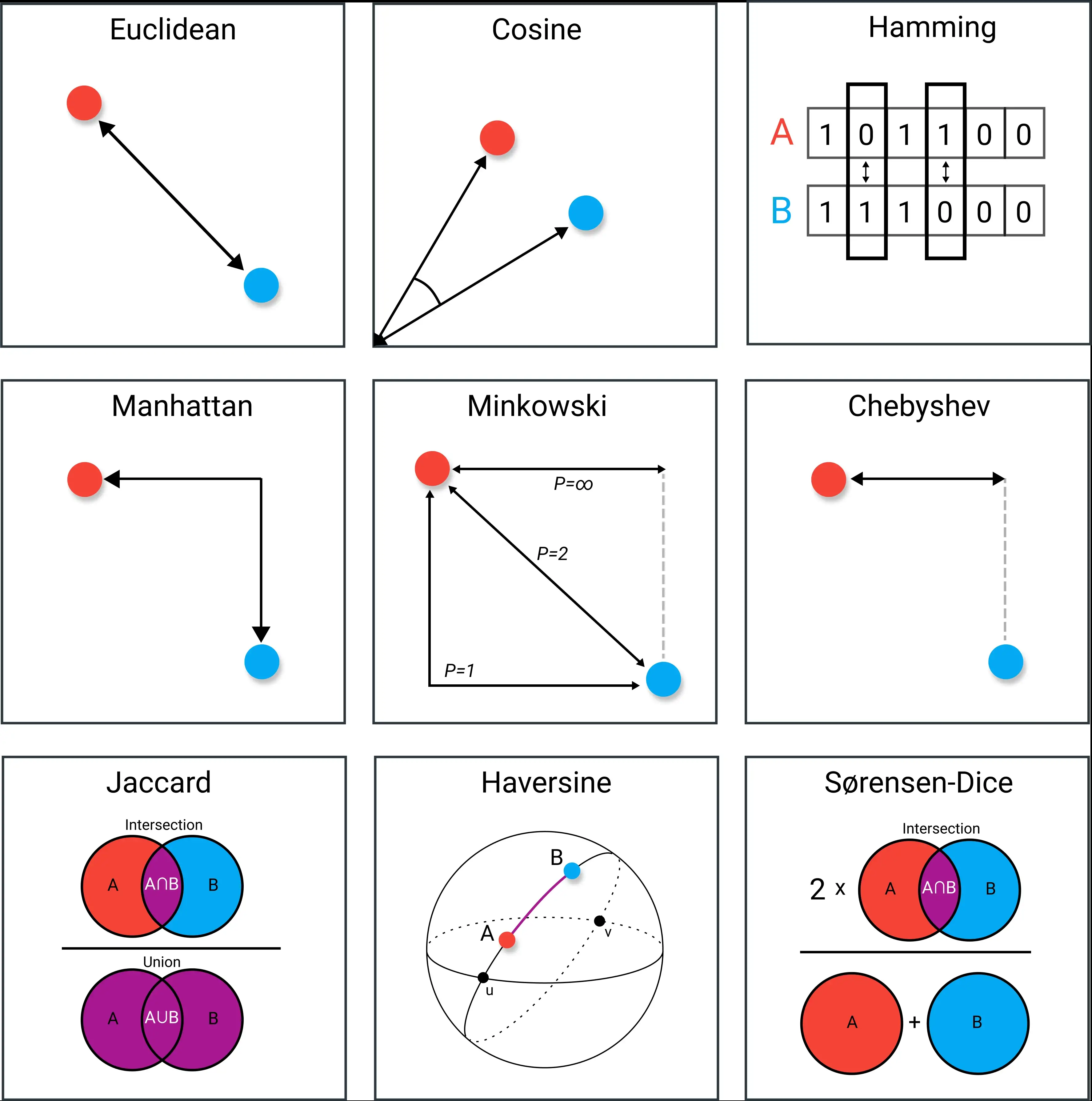
对于两个函数之间的距离，也可以有类似多种距离描述形式，函数\(f(x)\)到函数\(g(x)\)的距离：
(1) 情形1 \(d_{1}(f, g)= \displaystyle\int_{a}^{b}(f(x)-g(x))^{2} d x\)
(2) 情形2 \(d_{2}(f, g)=\displaystyle \max _{a \leq x<b}|f(x)-g(x)|\)
(3) 情形3 \(d_{3}(f, g)= \displaystyle \int_{a}^{b}(f(x)-g(x))^{k} d x\) (\(k\)取奇数的时候，要打上绝对值)
以上三种距离，它们之间不尽相同，确有着核心的共同点，抽象出来，就可以定义一个更一般的距离。我们现在有很多很多“距离”了，我们中学学的距离，两点间连线的长度，只是所有距离类型中的一类，我们现在要用属性来描述距离这一抽象的概念，即不能用“苹果”来描述，而用“水果”来描述距离。
- 你如何定义距离？
- 就对平面上的两个“点”
- 提示：不是具体指明它是什么，而是有什么“属性”的对象是它！
距离最重要的属性是什么？
(1) 大于或等于零(非负性)；
(2) 对称性；
(3) 三角不等式。
定义：设\(X\)是一非空集合，任给一对这一集合的元素\(x, y\) 都给定一个实数\(d(x, y)\)与它们对应，并且满足：
(1) 非负性 \(d(x, y) \geq 0, \quad d(x, y)=0 \Leftrightarrow x=y\)；
(2) 对称性 \(d(x, y)=d(y, x)\)；
(3) 三角不等式 \(d(x, y) \leq d(x, z)+d(z, y)\)
则称\(d(x, y)\)是这两点之间的距离。
注：折线定义距离(城区距离)也是对的(满足上面的条件)，比如把点放到平面直角坐标系，所谓的折线必须和坐标轴平行。
【度量空间】(Metric Space)，在数学中是指一个集合，并且该集合中的任意元素之间的距离是可定义的，亦称距离空间。
如果在集合\(X\)中再规定线性结构，就可以得到一个度量线性空间 (metric linear space)。
线性空间
【线性结构】：老师这里其实想说的是【线性空间】，必须满足八条规则。
【向量空间】是现代数学中的一个基本概念，是线性代数研究的基本对象，是指一组向量及相关的运算即向量加法，标量乘法，以及对运算的一些限制如封闭性，结合律。在现代数学中，向量的概念不仅限于此，满足下列公理的任何数学对象都可被当作向量处理，这时候其实就是将几何意义上的向量推广到了一般意义上的向量(除了数以外，还可以是矩阵、函数等等)，比如说一个函数空间也可以是一个向量空间，只要这个空间中的函数之间满足向量(线性)空间的全部性质。
The motivation for the definition of a vector space comes from properties of addition and scalar multiplication in \(\mathbf{F}^{n}\).
集合加法(addition)/标量乘法(scalar multiplication)的定义：
- An addition on a set \(V\) is a function that assigns an element \(u+v \in V\) to each pair of elements \(u, v \in V\).
- A scalar multiplication on a set \(V\) is a function that assigns an element \(\lambda v \in V\) to each \(\lambda \in \mathbf{F}\) and each \(v \in V\).
- 注：\(\mathbf{F}\)为数域，定义为实数或者复数均可。
- 注：这里是默认向量空间为set \(V\)。
线性空间的定义如下：(Linear Algebra Done Right的定义)
集合\(V\)满足以下性质才构成向量空间：
(1) 向量加法的结合律、交换律、单位元、逆元素；
(2) 标量乘法与标量的域乘法相容\(a(b \mathbf{v})=(a b) \mathbf{v}\)、标量乘法的单位元、标量乘法对向量加法的分配律\(a(\mathbf{u}+\mathbf{v})=a \mathbf{u}+a \mathbf{v}\)、标量乘法对域加法的分配律\((a+b) \mathbf{v}=a \mathbf{v}+b \mathbf{v}\)。
拓展：
(1) 狭义来说，如果\( u\)和\(w\)都是实数意义上的任意\(n\)维向量满足上面的条件，那么张成的空间是\(n\)维向量空间，记为\( \mathbb{R}^{n}\)。
(1) 线性空间 = 向量空间。
(1) 矩阵也可以看作是线性空间的“向量”，比如实数域上的全体\(m \times n\)矩阵，对于矩阵的加法数乘运算构成实数域上的线性空间，记作\(R^{m \times n}\)。
(1) 逆元素有加分的逆元素(取负号)和乘法的逆元素(倒数)，由于线性空间并不定义向量的乘积(内积空间从属于向量空间)，所以也就没有所谓的除法，即没有乘法意义上的逆元素。
也可以从【域】(Field)和【群】(group)的角度去定义线性空间，我们先了解以下什么是域。
域是满足以下三条公理的系统，记为\(\{F,+, \cdot\}\)：
(1) 系统\(\{F,+\}\)是一个具有单位元素\(0\)的Abel群；
(2) 设\(F^{\prime}\)是除\(x=0\)以外的所有\(x \in F\)的集合，则系统\(\left\{F^{\prime},\right\}\)是一个具有单位元素\(e\)的Abel群；
(3) 相对于\(+\)，满足分配律，即\(a \cdot(b+c)=a \cdot b+a \cdot c\)。
所有有理数集合、实数集合、复数集合，相对于普通的加法和乘法都构成了域。有了域的概念我们就可以定义线性空间：
(1) 在非空集合\(V\)内的任一对元素间定义加法的运算，使\(x=0\)构成Abel群(单位元素用\(\{V,+\}\)表示，\(x\)的逆元素用\(-x\)表示)，满足之前说的四条；
(2) 在数域\(F\)中的数与\(V\)中的元素之间定义一个纯量乘法运算，对\(F\)中任意数\(\alpha\)与\(V\)中的任一元素\(x\)，都可以由该运算唯一决定\(V\)中的一个元素\(y\)，记为\(y=\alpha x\)，数乘满足之前说的四条(标量乘法与标量的域乘法相容、标量乘法的单位元、标量乘法对向量加法的分配律、标量乘法对域加法的分配律)，则称\(V\)是数域\(F\)上的线性空间。(参考资料)
在抽象代数中，域是一种集合，在这个集合中可以对集合的非零元素进行加减乘除，其运算的定义与行为就如同有理数还有实数一样。域的概念是数域以及四则运算的推广。因此域是一个广泛运用在代数、数论还有其他数学领域中的代数结构。非正式的讲，域是种集合，集合中的元素可以做两种运算，“加法”和"乘法"，而且对集合中的任意元素都存在对应的加法逆元，乘法逆元，这种性质让我们可以定义加法和乘法的反运算。来自维基。
(线性)赋范空间(范数)
范数定义：如果\(V\)是数域\(F\)上的线性空间，且对于\(V\)中任意一个向量\(x\)，对应着一个实值函数\(\|x\|\)，它满足：
(1) 正定性：\(\|x\| \geq 0 ;\|x\|=0 \Leftrightarrow x=0\)
(2) 齐次性：\(\|\alpha x\|=|\alpha| \cdot\|x\| , \forall \alpha \in F\)
(3) 三角不等式：\(\|x+y\| \leq\|x\|+\|y\|, \, \forall x, y \in V\)
则称\(\|x\|\)为\(V\)上向量\(x\)的【范数】(norm)
\(x=(x_{1}, \cdots, x_{n})\)到零点的距离等价于范数：
(1) 情形1，\(\mathbb{R}^n\)上最符合直觉的长度，\(\|x\|=\sqrt{x_{1}^{2}+\cdots+x_{n}^{2}}\)
(2) 情形2，绝对值范数是曼哈顿范数的特殊形式，\(\|x\|=|x_{1}|+\cdots+|x_{n}|\)
(3) 情形3， \(\|x\|=\max \{|x,|, \cdots,|x_{0}|\}\)
由范数可以定义距离：\(d(x, y)=\|x-y\|\)，范数定义的表达式满足距离定义中的三点要求。
由距离不一定可以定义范数：比如\(\|x\|=d(0, x)\)，但\(\|\alpha x\|=d(0, \alpha x) \neq|\alpha|\|x\|\)。
上面的\(\alpha \)不能提出来，因为我们看距离的定义的时候，你不能够提出来，所以这里有一个需要特别强调的事情，就是我们一旦定义了抽象的距离，就不能用我们习惯的中学的距离的定义去理解它(中学里这里的\(\alpha \)可以提出来)，但是刚才给的距离没有这一条，只能按照前面有关距离的三条公理去推导其它性质。
- 范数可以简单看成到零点的距离多少；
- 范数相比于距离的内涵多了，同时指代的对象少了；
- 范数用于比较不同元素(向量)的大小；
- 定义了范数的线性空间(只能在线性空间上定义范数)就叫【线性赋范空间】(Normed vector space)；
- 线性赋范空间 = 赋范空间，In mathematics, a normed vector space or normed space is a vector space over the real or complex numbers, on which a norm is defined.
内积空间—夹角
赋范空间有向量的模长，即范数，但是还缺乏一个很重要的概念—两个向量的夹角，为克服这一缺陷，我们引入内积的概念。
定义：设\( (x,y, z) \in \mathbf{R}\)，且满足如下的条件，则称\((x, y)\)为【内积】：
(1) 对称性；如果是复数域上的，那么是共轭对称\(\langle x, y\rangle=\overline{\langle y, x\rangle}\)
(2) 对第一变元的线性性；\( \langle a x, y\rangle=a\langle x, y\rangle \quad \langle x+y, z\rangle=\langle x, z\rangle+\langle y, z\rangle\)
(3) 正定性；如果元素不是零，那么自己和自己内积一定大于零。
- 内积可以导出范数：\(\|x\|^{2}=(x, x)\)；
- 在线性空间上定义内积，其空间称为【内积空间】(Inner product space)；
- 柯西-施瓦茨不等式(Cauchy–Schwarz inequality)，对于一个内积空间的向量\(x\)和\( y\)有\(|\langle x, y\rangle|^{2} \leq\langle x, x\rangle \cdot\langle y, y\rangle\)，等价地，将两边开方，等式右边即可以写为两向量范数乘积的形式\(|\langle x, y\rangle| \leq\|x\| \cdot\|y\|\)。
欧几里得空间
内积可在空间中建立欧几里得几何学，例如交角、垂直和投影等，故习惯上称其为【欧几里得空间】。
正交：\( (x, y)=\displaystyle\sum_{k=1}^{n} x_{k} y_{k}=0\) 夹角：\(\cos \theta = \displaystyle\frac {(x,y) }{\|x\| \cdot\|y\|}\)
欧几里得空间从属于内积空间，(来自知乎白如冰)定义如下：设\(V\)是实数域\(\mathbf{R}\)上一个向量空间，如果对于\(V\)中，任意一对向量\(\boldsymbol\xi, \boldsymbol\eta\)，有一个确定的记作\(\langle\boldsymbol\xi, \boldsymbol\eta\rangle\)的实数与它们对应，叫作向量\((\boldsymbol\xi\)与\(\boldsymbol{\eta}\)的内积(或标量积)，并且下列条件被满足：
(1) \(\langle\boldsymbol{\xi}, \boldsymbol{\eta}\rangle=\langle\boldsymbol{\eta}, \boldsymbol{\xi}\rangle\)
(2) \(\langle\boldsymbol{\xi}+\boldsymbol{\eta}, \boldsymbol{\zeta}\rangle=\langle\boldsymbol{\xi}, \boldsymbol{\zeta}\rangle+\langle\boldsymbol{\eta}, \boldsymbol{\zeta}\rangle\)
(3) \(\langle a\boldsymbol{ \xi}, \boldsymbol{\eta}\rangle=a\langle\boldsymbol{\xi}, \boldsymbol{\eta}\rangle\)
(4) 当\(\boldsymbol{\xi}\neq 0\) 时, \(\langle\boldsymbol{\xi}, \boldsymbol{\xi}\rangle>0\)
这里\( \boldsymbol{\xi}\)，\(\boldsymbol{\eta}\)，\(\boldsymbol\zeta\)是\(V\)的任意向量，\(a\)是任意实数，那么\(V\)叫作对这个内积来说的欧几里得空间(欧式空间)。
欧氏空间也称为「欧几里得空间」，可以理解为几何空间的度量在线性空间推广的结果，直白地说，欧式空间是一个有「内积」的线性空间，引入内积的目的是为了能够计算两点间的距离和夹角。(来自知乎宫非)
其他
【希尔伯特空间】(Hilbert space)：1904年-1910年，希尔伯特引入无穷实数组并定义内积，其空间称为内积空间，再加上完备性，称为希尔伯特空间(无穷维)；
【巴拿赫空间】(Banach space)：1922年巴拿赫提出赋范空间，其完备的赋范空间称为巴拿赫空间；
巴拿赫空间实例：自然界本身是没有「颜色」这个属性的，只有对不同波长光线的反射率/透过率，到达人眼中的，显然是一个连续的光谱分布函数。数学上，这是一个无穷维的函数空间—巴拿赫空间。而人眼内的三种视锥细胞，它们的感光特性曲线相当于是在这个无穷维的函数空间中建立了三个基底。任何一个光谱分布进来，三种视锥细胞被激发。由于色视觉响应的线性性，这一过程相当于光谱分布函数与三个基底做内积，或者说，「投影」到这三个基底上。(参考色彩空间基础—章佳杰)
【完备性】：空间在极限运算中，取极限不能跑出去，就是说相当于我们原来做极限的时候，有理数集不行，一定要取到实数集。一个度量空间\(X\)中的所有柯西数列都会收敛到\(X\)中的一点，那么\(X\)被称为是一个完备空间。(参考这里)
【柯西列】就是空间中元素构成的一个序列，并且这个序列在无穷远处两个元素之间的距离趋于零。准确的说，如果空间中有一个序列\(\left\{x_{n}\right\}\)，当\(n, m \rightarrow \infty\)时，\(d\left(x_{n}, x_{m}\right) \rightarrow 0\)，则\(\left\{x_{n}\right\}\)就是一个柯西列，也就是说完备性保证了序列取极限不会跑到空间外面去。任何收敛数列必然是柯西列，任何柯西列必然是有界序列。
柯西列的定义依赖于距离的定义，所以只有在度量空间中柯西列才有意义。柯西列一个重要性质是，在完备空间中，所有的柯西数列都有极限且极限在这空间里，这就让人们可以在不求出这个极限（如果存在）的情况下，利用柯西列的判别法则证明该数列的极限是存在的。柯西列在构造具有完备性的代数结构的过程中也有重要价值，如构造实数。
下左图：一个柯西序列\(\left(x_n\right)\)的绘图，使用蓝色，\(x_n\)相对于\(n\)。 如果包含这个序列的空间是完备的，则这个序列的"最终目标"也就是极限存在。
下右图：非柯西的一个序列。这个序列的元素不能随着序列前进而相互靠近。
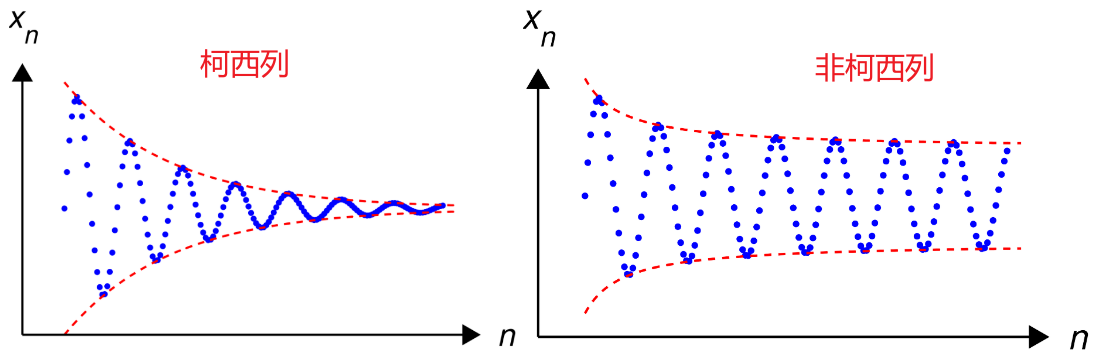
实数系是完备的，整数系、有理数系是不完备的。
有理数\(\mathbb{Q}\)在通常定义的距离意义下不是完备的：存在某个由有理数组成的序列，收敛到某个无理数，所以这数列在有理数这空间是不收敛的。比如：
(1) 如下定义的序列: \(x_0=1, x_{n+1}=\left(x_n+2 / x_n\right) / 2\) ，即 \((1,3 / 2,17 / 12, \ldots)\) 。可以证明这个序列收敛到一个无理数\(\sqrt{2}\)。
(2) 对于每个给定的\(x \neq 0\)而言，以下函数\(\exp (x), \sin (x), \cos (x)\) 的值都可以表示为一个有理数序列的极限，但当\(x\)为有理数时，这个值却是无理数。
实数的完备性，是指实数能满足确界原理/单调有界原理/柯西收敛定理/区间套定理/有限覆盖定理的一种特性。上述几个定理在本质上是等价的（即能够相互推证），以柯西收敛定理为例： 有理的柯西列的极限未必是有理数，这说明柯西收敛定理在有理数集不能成立，这就反映了有理数的不完备性。但柯西收敛定理保证实柯西列的极限仍是实数，这就反映了实数的完备性。(参考这里)
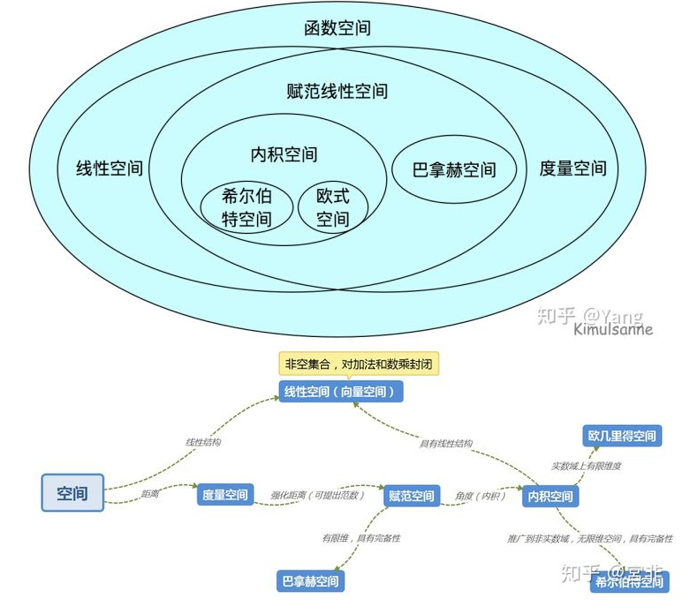
集合 + 距离 = 度量空间
集合 + 线性 = 线性空间
线性空间 + 范数(度量空间) = 赋范线性空间
赋范线性空间 + 内积 = 内积空间
内积空间 + 完备 = 希尔伯特空间
赋范线性空间 + 完备 = 巴拿赫空间
参考资料：
1. 内积、点积、数量积有何区别？— 知乎
2. 希尔伯特空间(推荐)-知乎
3. 如何通俗地解释欧氏空间？— 知乎
4. 如何理解并区分线性空间、向量空间、矩阵空间这三个数学概念？— 知乎
5. 从度量空间、线性空间到希尔伯特空间 — 知乎
6. 【线性代数】 08 - 线性空间的度量
7. 数学之旅 各种空间 整理笔记
8. 学点数学(3)-函数空间
拓扑空间
xx
对偶空间-(映射/泛函)
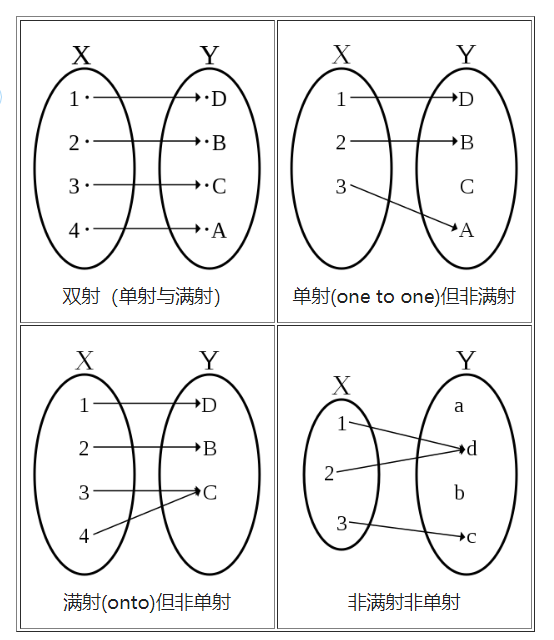【映射】(map)：在集合论中设\(A, B\)是两个非空集合，若对\(A\)中的任一元素\(x\)，依照某种规律 (或法则) \(f\)，恒有\(B\)中的唯一确定的元素\(y\)与之对应，则称对应规律\(f\)为一个从\(A\)到\(B\)的映射。 记作：\(f: A \rightarrow B\) ，有时记: \(f: x \mapsto y\)。更细的分类如图：
【线性映射】：Let \({\displaystyle V} \) and \({\displaystyle W} \) be vector spaces over the same field \({\displaystyle K}\). A function \({\displaystyle f:V\to W}\) is said to be a linear map if for any two vectors \( {\textstyle \mathbf {u} ,\mathbf {v} \in V}\) and any scalar \( {\displaystyle c\in K}\) the following two conditions are satisfied:
Additivity: \(f(\mathbf{u}+\mathbf{v})=f(\mathbf{u})+f(\mathbf{v})\)
Homogeneity: \(f(c \mathbf{u})=c f(\mathbf{u})\)
进一步可以推广$$f\left(c_{1} \mathbf{u}_{1}+\cdots+c_{n} \mathbf{u}_{n}\right)=c_{1} f\left(\mathbf{u}_{1}\right)+\cdots+c_{n} f\left(\mathbf{u}_{n}\right)$$
【泛函】(functional)通常是指定义域为函数集，而值域为实数或者复数的映射，换句话说，它是从函数组成的一个向量空间到标量域的映射，它的输入为函数，而输出为标量。
注：\( \mapsto\)这个符号的英文名叫Maps to，翻译过来就是映为。\(f: a \mapsto b\) means the function \(f\) maps the element \(a\) to the element \(b\).
泛函和函数、算子的概念区别：
(1) 算子是一个函数到另一个函数的映射，它是从向量空间到向量空间的映射。
(2) 泛函是从向量空间到数域的映射。
(3) 函数是从数域到数域的映射。
泛函的例子：二维平面空间，从坐标原点到点\((a,b)\)的连接曲线是\( y=y(x)\)，曲线的弧长微元是\(d s=\sqrt{1+(\displaystyle \frac{d y}{d x})^{2}} d x\)，曲线的总弧长是\(s=\displaystyle \int_{0}^{a}(1+y^{\prime 2})^{1 / 2} d x\)，其中\( s\)是标量，该式右边是\(y^{\prime}(x)\)的广义函数，被称为泛函，可记为\(s(y^{\prime})\)。
问题就变成了：找出曲线\( y=y(x)\)，使得泛函\(s(y^{\prime})\)最小。这个问题可以用变分法求解
参考资料：
(1) 如何评价「泛函、映射、算子、变换都是函数，是搞数学的人骗普通人的把戏」这一说法？实际情况如何？-知乎
(2) 能不能把泛函简单地理解为函数？-知乎
(3) 算子这个词的来源以及意义，有什么作用，为什么可以这样用？—知乎
【线性泛函】：In mathematics, a linear form (also known as a linear functional, a one-form, or a covector 余向量) is a linear map from a vector space to its field of scalars (often, the real numbers or the complex numbers).
\(\mathbf{F}\) denotes either \(\mathbf{R}\) or \(\mathbf{C}\). \(V\) and \(W\) denote vector spaces over \(\mathbf{F}\). A linear functional on \(V\) is a linear map from \(V\) to \(\mathbf{F}\). In other words, a linear functional is an element of \(\mathcal{L}(V, \mathbf{F})\).
线性泛函的例子：
- Define \(\varphi: \mathbf{R}^3 \rightarrow \mathbf{R}\) by \(\varphi(x, y, z)=4 x-5 y+2 z\). Then \(\varphi\) is a linear functional on \(\mathbf{R}^3\).
- Fix \(\left(b_1, \ldots, b_n\right) \in \mathbf{C}^n\). Define \(\varphi: \mathbf{C}^n \rightarrow \mathbf{C}\) by $$ \varphi\left(z_1, \ldots, z_n\right)=b_1 z_1+\cdots+b_n z_n . $$ Then \(\varphi\) is a linear functional on \(\mathbf{C}^n\).
- Define \(\varphi: \mathcal{P}(\mathbf{R}) \rightarrow \mathbf{R}\) by \(\varphi(p)=3 p^{\prime \prime}(5)+7 p(4)\). Then \(\varphi\) is a linear functional on \(\mathcal{P}(\mathbf{R})\).
- Define \(\varphi: \mathcal{P}(\mathbf{R}) \rightarrow \mathbf{R}\) by \(\varphi(p)=\displaystyle\int_0^1 p(x) d x\). Then \(\varphi\) is a linear functional on \(\mathcal{P}(\mathbf{R})\).
- 量子力学中的线性泛函。线性泛函在量子力学中特别重要。量子力学系统以跟其对偶空间共轭同构的希尔伯特空间表示。系统的一个态可以一线性泛函表示。详见狄拉克符号。
- 统计学上的分布。在广义函数的理论，分布可以视为测试函数空间的线性泛函。
【对偶空间】：The dual space of \(V\), denoted \(V^{\prime}\), is the vector space of all linear functionals on \(V\). In other words, \(V^{\prime}=\mathcal{L}(V, \mathbf{F})\).
对偶空间的实例：
- 信号处理中时域函数(空间)和对应的频域函数(空间)就是一对对偶空间；
- 量子力学中坐标空间波函数和动量空间波函数就是一对对偶空间；
- 固体物理中实空间格子和虚拟的倒空间的格子就是一对对偶空间；
上面的例子的本质还是傅里叶变换，傅里叶变换的对偶性也可以正变换和逆变换公式的相似性中窥探一二，在笔记傅里叶变换及其应用中我们谈到了几个关于傅里叶变换的对偶定理，我认为最能表现对偶性的是\(\mathcal{F F} f=\mathcal{F}(\mathcal{F} f)=\mathcal{F}\left(\mathcal{F}^{-}\left(f^{-}\right)\right)=f^{-}\)，即对函数进行两次傅里叶变换等于该函数的反转。
对偶空间更具体的描述：假设实坐标空间\(\mathbf{R}^{n}\)内的向量用列向量来表示：\(\vec{x}=\left[\begin{array}{c} x_{1} \\ \vdots \\ x_{n} \end{array}\right]\)那么这些坐标中的任何线性泛函都可以用以下形式的和来表示：$$f(\vec{x})=\left[a_{1} \ldots a_{n}\right]\left[\begin{array}{c} x_{1} \\ \vdots \\ x_{n} \end{array}\right]=a_{1} x_{1}+\cdots+a_{n} x_{n}$$此时行向量\(\vec{a}=\left[a_1 \ldots a_n\right]\)相当于遍历了\(\mathbf{R}^{n}\)上所有的列向量，通过内积运算将其映射到数域\(\mathbf{R}^{n}\)。每一个不同的\(\vec{a}\)就是不同的映射，换句话说每一个行向量就是映射本身，行向量把列向量映射成一个实数(线性泛函的映射)，。所有不同的\(\vec{a}\)(映射)组成的集合，构成了一个新的向量空间，就是列向量\(\vec{x}\)所处向量空间的对偶空间。行向量\(\vec{a}\)和列向量\(\vec{x}\)互为【对偶向量】，所有行向量张成的空间和所有列向量张成的空间互为对偶空间。这里讨论的是\(\mathbf{R}^{n}\)上的向量空间，实际的向量空间可以是更一般的情况，比如连续的函数的集合组成的向量空间。
假设两个对偶向量的内积写为\(\langle \vec{v^{*}}, \vec{v}\rangle\)，行向量和列向量分别对应两个相互对偶的空间\(V^*\)和\(V\)，且\(V\)为线性空间，我们这里可以简单证明一下\(V^*\)也是线性空间：
(1) 零向量：\(\langle \vec{0^{*}}, \vec{v}\rangle=0\)
(2) 复向量：\(\langle -\vec{v^{*}}, \vec{v}\rangle=-\langle \vec{v^{*}}, \vec{v}\rangle\)
(3) 数乘：\( \langle k\vec{v^{*}}, \vec{v}\rangle=k\langle \vec{v^{*}}, \vec{v}\rangle\)
从上面的例子也可以看到行向量和列向量互相映射成一个实数，既可以理解为\(\vec{v^{*}}\)把\(\vec{v}\)映射为一个实数，也可以理解为\(\vec{v}\)把\(\vec{v^{*}}\)映射为一个实数。很容易发现两次对偶之后，回到原来的向量空间$$V \rightarrow V^* \rightarrow V^{**}=V$$从范畴论的角度又是如何理解对偶，看wiki
对偶空间参考资料：
1. 知乎-怎么形象地理解对偶空间（Dual Vector Space）？
2. 对偶空间 目录
3. 看了这篇文章你还不能理解对偶空间算我输
4. 物理学咬文嚼字之二十四-对偶
对偶问题
优化理论中的对偶，线性规划等等
\(L^p\)空间
流形简介
xx
参考资料：
(1) 知乎
不动点理论
混沌与分形