参考资料:
(1) 振动和波8.03学习笔记
(2) 麻省理工MIT-官网
(3) 课程视频-Yen-Jie Lee
(4) 课程视频-Walter Lewin
(5) 北京师范大学-涂展春-力学-PPT
基础知识
波的公式\(y(x, t)=A \sin (k x + \omega t)\),有时候又写成\(y(x, t)=A \sin (k x - \omega t)\),当\( x\)和\(t\)前面的系数是opposite sign,说明the wave is traveling in positive \( x\)-direction,否则说明波向负方向传播。其中\(k x\)反映的是空间周期性,\(\omega t\)反映时间周期性。
我们先回忆什么叫【波阵面】(wave surface )或者说【波面】,同一个波面上的点距离振动源的距离相等(整个体系都处在均一介质中),因此振动的相位相等。【波前】(wave front)是传到最前面的那个波面。根据波前或者波阵面的形状,可以将波分为下面三种类型。
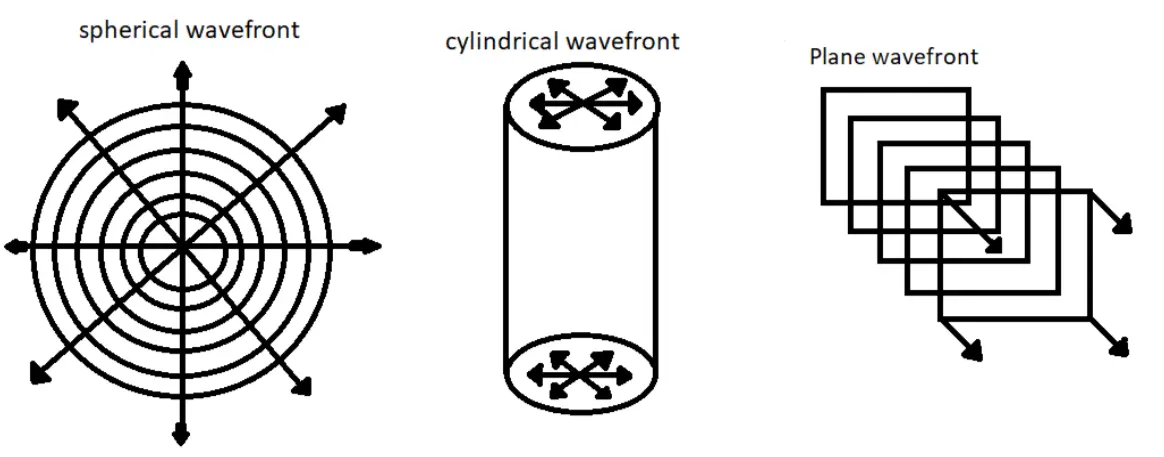
上面都是都是理想状态波的传播类型,实际是不可能存在的,但是现实生活中很多实例可以近似看成这些类型。
- 球面波(spherical wave)——如果传播距离远大于光源本身的尺寸时,我们就可以把光波当成球面波(比如考虑太阳光的能量辐射,完全可以把太阳看成质点)。
- 柱面波(cylindrical wave)——比如无限长线电流源。交通繁忙的公路上,汽车往往连成一条线行驶,这些汽车可认为是线声源,所辐射的噪声就是柱面波。
- 平面波(plane wave)——当然如果对地球上很小的一块面积来说,我们又可以把太阳光看成是平行光,那么这个时候就可以当做平面波处理。平面波能量不扩散,振幅为常数。
【波速】实质上是相位传播的速度,故称为相速度;其大小主要决定于媒介的性质,与波的频率无关(后面我们会讨论和频率有关的情况,即色散)。
- 拉紧的绳子或弦线中横波的波速度为\(\sqrt{\displaystyle\frac{T}{\mu}}\),其中\(T\)为张力,\(\mu\)为线密度。
- 均匀细棒中,纵波的波速为\(\sqrt{\displaystyle\frac{Y}{\rho}}\),其中\(Y\)为固体棒的杨氏模量,\(\rho\)为固体棒的密度。
- 固体媒质中传播的横波速率为\(\sqrt{\displaystyle\frac{G}{\rho}}\),其中\(G\)为固体的切变弹性模量,\(\rho\)为固体的密度。
- 液体和气体只能传播纵波(特殊情况后面也有讨论),其波速为\(\sqrt{\displaystyle\frac{B}{\rho}}\),其中\(B\)为流体的容变弹性模量,\(\rho\)为流体的密度。
- 稀薄大气中,纵波的波速为\(\sqrt{\displaystyle\frac{\gamma R T}{M}}\),其中\(\gamma\)为气体摩尔热容比,\(M\)为气体摩尔质量,\(R\)为气体摩尔常数。
这里需要补充各种波的表达式,参考这里
大学物理学公众号的科普:
再谈平面波
实际上波可以是任何形状的,比如球面波,方波,三角波以及波包(wave packet)等等。其中最简单的就是【简谐平面波】(sinusoidal plane wave)。简谐平面波是一种最简单、最基本的波,研究简谐波的波动规律是研究更复杂波的基础。在任意时刻,它在传播方向的波形是一个简谐函数,即正弦或余弦平移一个相位,且范围是无穷大。“平面” 这个词的由来是因为三维空间中其等相位面都是平面(见下文),但广义来说平面波所在的空间可以是任意维度的。简谐平面波都往往被简称为"简谐波"或者"平面波"。广义来说,平面波未必是简谐的,而简谐波也未必是平面的。无论是横波还是纵波,都可以表示为:\(y(x, t)=A \cos \left(k x-\omega t+\phi_0\right)\)。对于横波来说,振幅\(A\)对应于质点振动垂直于波矢(波的传播方向);对于纵波,振幅\(A\)对应于质点振动与波矢方向相同。广义来说,振幅可以是一个任意方向的矢量\(\mathbf{A}\),它可以既不平行也不垂直于传播方向,此时它可以认为是横波和纵波的叠加。
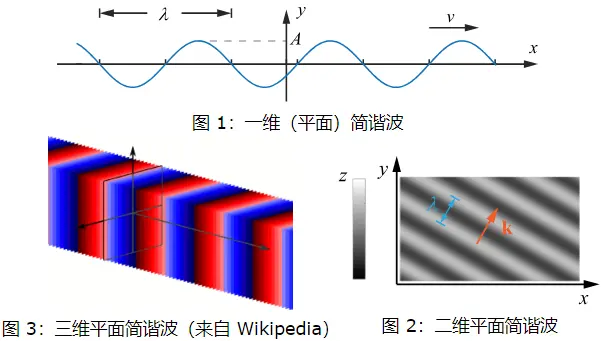
对波动方程\(y(x, t)=A \cos \left(k x-\omega t+\phi_0\right)\)求\(x\)和\(t\)的二阶偏导数可得平面波的波动方程$$ \frac{\partial^2 y}{\partial x^2}=\frac{1}{u^2} \frac{\partial^2 y}{\partial t^2} $$任何平面波可分解为一系列不同频率的简谐波,故都满足这一方程。其中\(u=\displaystyle\frac { \omega }{k} \)就是这一平面波的传播速度。
A plane wave has a well defined direction of propagation with no divergence.(来自rp-photonics)
等待补充
参考资料:
(1) 平面简谐波—小时百科
(2) Plane Waves—rp-photonics
(3) 平面简谐波的波函数—大学物理课件
(4) 波动方程的平面波解,球面波解及柱面波解
横波与纵波
波的分类:机械波(透过介质才能传播),电磁波,引力波不需要介质。对于机械波,又可以分为横波、纵波和面波。
横波:
- Particles vibrate in a direction perpendicular to the direction of propagation of the wave.
- Crests and troughs are formed.
- Formed on the surface of solids and liquids.
- May be elastic waves or non elastic waves eg.light wave,radio wave.
- Do not create pressure difference in the medium.
纵波:
- Particles vibrate in a direction parallel to the direction of propagation of the wave.
- Compression and rarefacations are formed.
- Formed in solids,liquids and gas.
- Only elastic waves (mechanical)eg.sound wave,seismic wave.
- Creates pressure difference in the medium.
【理想流体】(ideal fluid):没有剪应力(shear stress)、黏度和热传导等性质。
【声波】声波有横有纵,但大部分是纵波,要看传播的介质。声音在空气传播是纵波,因为声音在传播过程中是空气(介质)发生膨胀和收缩是沿着声波传播方向的。声音通过金属等介质传播,则是横波,是上下振动,速度较快。横波的话,以一个质点为例,振动源的振动,不断向四周扩散,周围空间的质点在各自位置上振动,并不向波传播的方向移动。
【电磁波】:in free-space or other uniform isotropic dielectrics, electromagnetic waves are strictly transverse. However electromagnetic waves can display a longitudinal component in the electric and/or magnetic fields when traversing birefringent materials, or inhomogeneous materials especially at interfaces (surface waves for instance) such as Zenneck waves. 比如TE/TM/TEM mode?
【机械横波】:Transverse waves commonly occur in elastic solids due to the shear stress generated; the oscillations in this case are the displacement of the solid particles away from their relaxed position, in directions perpendicular to the propagation of the wave. These displacements correspond to a local shear deformation of the material. Hence a transverse wave of this nature is called a 【shear wave】. Since fluids cannot resist shear forces while at rest, propagation of transverse waves inside the bulk of fluids is not possible.
- 横波机械波一般认为难以在液体气体中传播是因为这些介质有容变无切变,难以有切应力。但是实际流体可能并不严格满足这种理想情况,所以会存在传播横波的可能性。而对于水而言,其表面张力的效果也给水面传播横波提供了可能。
- 横波的振动方向与传播方向垂直,说明当横波在介质中传播时,介质中层与层之间将发生相对位错,即产生切变。只有固体能承受切变,因此横波只能在固体中传播。在液面上因有表面张力,故能承受切变,所以液面波是纵波与横波的合成波。此时,组成液体的微元在自己的平衡位置附近做椭圆运动。
- 非牛顿流体也可以存在横波。
- 不存在横波的是无粘性的"理想流体"。
- The ripples in a pond can be analyzed as a combination of transverse and longitudinal waves (gravity waves) that propagate together.
- In seismology, shear waves are also called secondary waves or S-waves.
参考:既然横波(机械波)只能在固体中传播,那么为什么水波中还含有横波?—知乎
【机械纵波】:Mechanical longitudinal waves are also called compressional or compression waves, because they produce compression and rarefaction when traveling through a medium, and pressure waves, because they produce increases and decreases in pressure. A wave along the length of a stretched Slinky toy, where the distance between coils increases and decreases, is a good visualization. Real-world examples include sound waves (vibrations in pressure, a particle of displacement, and particle velocity propagated in an elastic medium) and seismic P-waves (created by earthquakes and explosions). The other main type of wave is the transverse wave, in which the displacements of the medium are at right angles to the direction of propagation.
地震波
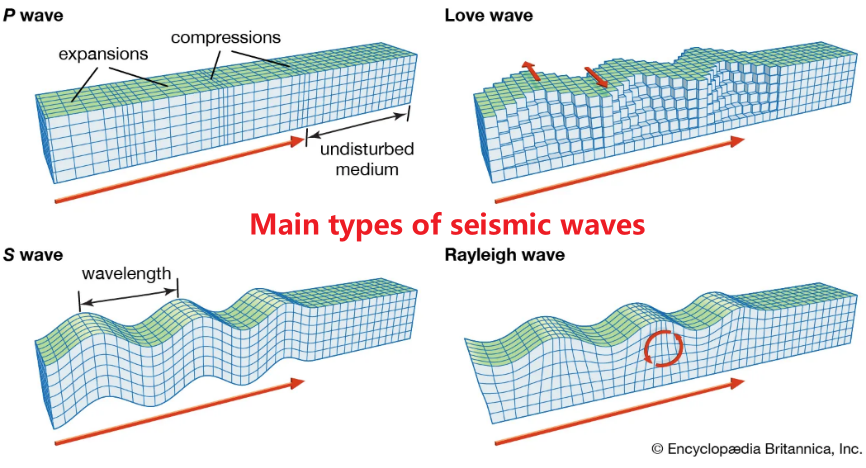
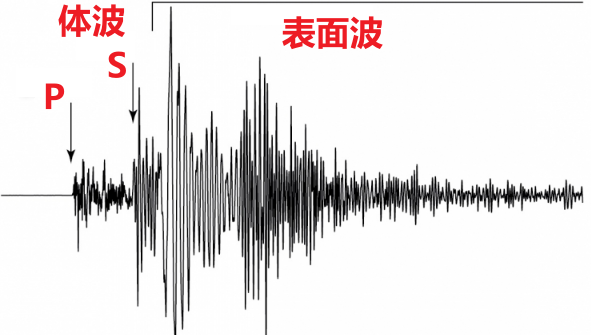
地震波:S波及其衍生的表面波是造成破坏的主要原因。
- 【实体波】:暂不讨论T波
- 【P波】: P代表Primary或Pressure。P波被称为主要是因为P波的传播来自于在传播方向上施加压力,而地球内部几乎不可压缩,因此P波很容易通过介质传递能量,故其震动最快、地震学应用相当高。事实上,P波是所有地震波里最快的波,因此也会是地震仪第一个记录到的波。因为压缩力在固体、液体中都能存在,因此P波能在固体和液体中传播。
- 【S波】: S代表Secondary剪力Shear。S波到来的比P波晚,同样是由地震的岩石错位直接产生。S波的震动方向平行于地表的分量较多,较容易水平拉扯建筑物,而一般建筑水平耐震能力较弱(因为垂直耸立),故S波经常是造成地震破坏的主因。
- 地震波中的纵波是由震源传出的压缩波,质点振动与波前进方向一致,一疏一密向前推进,周期短、振幅小。 而横波是震源向外传播的剪切波,质点振动方向与波前进方向相垂直,传播时介质体积不变但形状改变,周期较长振幅较大。 因此在相同介质、相传播距离的条件下,纵波就比横波的速度快。
- 【表面波】(Surface wave): Surface waves travel more slowly through Earth material at the planet's surface and are predominantly lower frequency than body waves. They are easily distinguished on a seismogram(震动图,由地震仪绘制). Shallow earthquakes produce stronger surface waves; the strength of the surface waves are reduced in deeper earthquakes. 我们下面只讨论主要的两种表面波:
- 【勒夫波】(Love wave): Love waves are horizontally polarized surface waves, and they produce entirely horizontal motion. The amplitude is largest at the surface and diminishes with greater depth. 由浅源地震所引起的勒夫波最明显。
- 【瑞利波】(Rayleigh waves): A Rayleigh wave rolls along the ground with a more complex motion than Love waves. Although Rayleigh waves appear to roll like waves on an ocean, the particle motion is opposite of ocean waves. Because it rolls, it moves the ground up and down, and forward and backward in the direction that the wave is moving. Most of the shaking felt from an earthquake is due to the Rayleigh wave, which can be much larger than the other waves. Like Love waves, the amplitude of the wave decreases dramatically with depth.
艾里波(Airy waves)理论
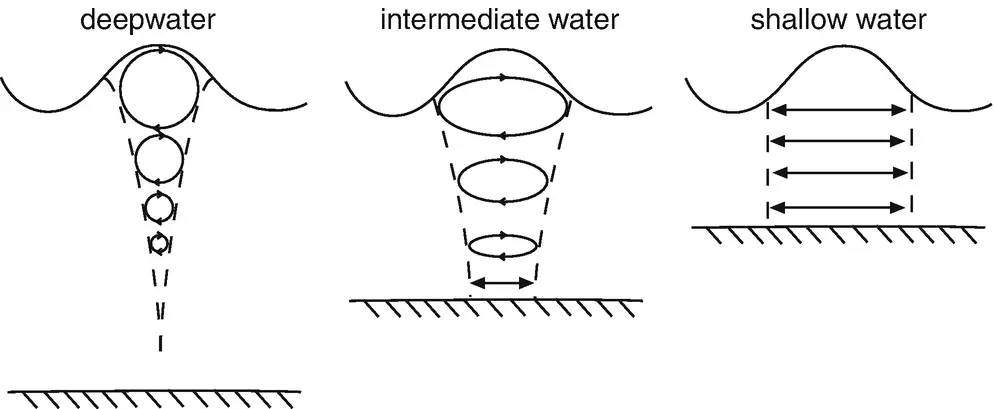
Description of the orbital motion of Airy waves in deep, intermediate, and shallow water. 其中第一种和第二种情形类似前面提到过的Rayleigh waves,既有上下的运动,也有前后的运动,所以既不是纯横波也不是纯纵波。这里主要反映的是水的密度不变性。
参考资料:
(1) Seismology—Michigan Tech
(2) 地震波—Wiki
(3) The study of earthquakes—britannica
(4) 李永乐讲地震—油管
Periodic Oscillations, Harmonic Oscillators
uniform circular motion 匀速圆周运动
- Sound wave
- Water wave
- Electromagnetic waves
- Brain waves
- Probability density waves
- Gravitational waves 引力波
We wouldn't even recognize the universe without using vibrations and waves.
很多物理中的基本单元都是用振动表示的,至于为什么振动和波在物理学中这么通用,没有人知道为什么,反正用振动的方法就是可以描述许多现象。
The most incomprehensible thing about the universe is that it is comprehensible. —Einstein
But in my opinion, everything in nature occurs mathematically. —Rene Descartes
振动和波的涵盖了经典力学,电磁学,光学,量子力学,通过本系列的学习你不仅会了解振动-波和以上学科的关系,还会学习一些他们的实际应用。通过本课程的学习,我们将学会:
- 如何将物理问题转化为数学问题
- 单谐波振荡 single harmonic oscillator
- 耦合震荡 coupled oscillator
- 波是无数个震荡组成的
- 波的傅里叶展开
- 用边界条件整合物理问题
- 与电磁波有关的现象
- 波在光学中的应用

根据牛顿定律:$$\vec{F}=m \vec{a}=m \frac{d^{2} x(t)}{d t^{2}} \hat{x}=m \ddot{x}(t) \hat{x}=-k x(t) \hat{x}$$Since everything is in the \(x\) direction we drop \(\hat{x}\)$$ \ddot{x}=-\frac{k}{m} x=-\omega^{2} x $$定义\(\omega \equiv \displaystyle\sqrt{\frac{k}{m}}\),微分方程的解为$$ x(t)=a \cos \omega t+b \sin \omega t $$如果知道initial conditions \(x(0)=x_{\text {Initial }} \) and \(\dot{x}(0)=0\)那么我们就可以确定\(a=x_{\text {Initial }}\),\(b=0\),于是最终的结果为$$ x(t)=x_{\text {Initial }} \cos (\omega t) $$Let’s stop for a second and consider what we have done:
(1) Take a physical situation and translate it to a mathematical description
(2) Solve the equation
(3) The solution actually matches what the nature does to the mass
上面讨论的是【胡克定律】(Hooke’s Law)的理想情况,实际上there is NO “Hooke’s Law”! The law breaks down at some point. But the law is a very good approximation when we consider small amplitude vibrations.
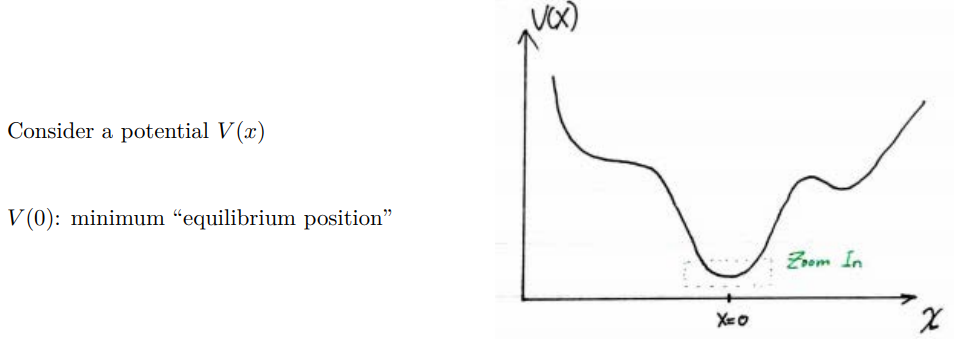
上图最低点的一阶导数为零。Consider a small oscillation about the equilibrium position: (泰勒展开)$$ F(x)=-\frac{d}{d x} V(x)=-V^{\prime}(0)-V^{\prime \prime}(0) x-\frac{1}{2} V^{\prime \prime \prime}(0) x^{2}+\cdots $$由于\(x\)很小,所以\(F(x) \approx-V^{\prime \prime}(0) x\)
This is a remarkable result: "Hooke's Law" works on "all systems with a smooth potential" (also \(V^{\prime \prime}(0) \neq 0\) ) for small oscillations about stable equilibrium! How small? The condition \(\left|x V^{\prime \prime \prime}(0)\right| \ll V^{\prime \prime}(0) \quad\) must be satisfied.
从线性到非线性的例子:如果两个相同的pendulum (/ˈpendʒələm/),如果开始的时候都拉到一个小角度位置(小于10 °,但是二者的角度不同),那么二者就会同周期地振荡,周期满足\(T=2 \pi \sqrt{\displaystyle\frac{l}{g}}\),即使二者的初始角度不同,但只要都很小的话,结果还是同周期地振荡。但是如果一个初始位置的角度大,另一个初始位置的角度小,那么会发现,越到后面越来越不同步了,这就是非线性项的影响。
对于线性运动的系统\(\ddot{x}+\omega^{2} x=0\)有两个重要的性质:
(1) 解的叠加性:\( x(t)=x_{1}(t)+x_{2}(t)\)也是解;
(2) Time translation invariance (时间平移不变性): If \(x(t)\) is a solution \(\Rightarrow x\left(t^{\prime}\right)=x(t+a)\) is also a solution.这是因为$$ \frac{d}{d x} x(t+a)=\left.\frac{d(t+a)}{d t} \frac{d x\left(t^{\prime}\right)}{d t^{\prime}}\right|_{t^{\prime}=t+a}=\left.\frac{d x\left(t^{\prime}\right)}{d t^{\prime}}\right|_{t^{\prime}=t+a} $$
This means that if I change \(t=0\) the physics will be the same! Most of the physics systems are time translation invariant in the absence of an external force. To break the symmetry(对称性破缺): need to make \(k\), the spring constant, (and thus \(\omega\) ) time dependent!
解的多种写法:
(1) \(x(t)=a \cos \omega t+b \sin \omega t\)
(2) \(x(t)=A \cos (\omega t+\phi)=(A \cos \phi) \cos \omega t-(A \sin \phi) \sin \omega t\)
(3) \(x(t)=\operatorname{Re}\left[A e^{i(\omega t+\phi)}\right]\).
In principle: $$ x(t)=\operatorname{Re}[A \cos (\omega t+\phi)+i f(t)] $$\(f(t)\) is an arbitrary real function. But if \(f(t)=A \sin (\omega t+\phi)\) amazing thing happens!
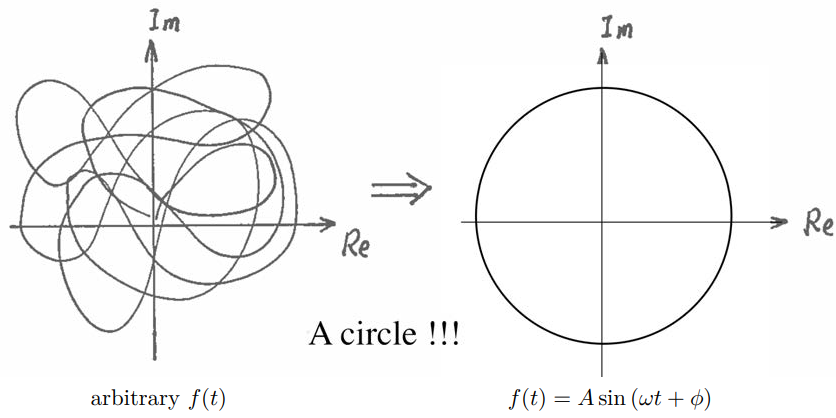
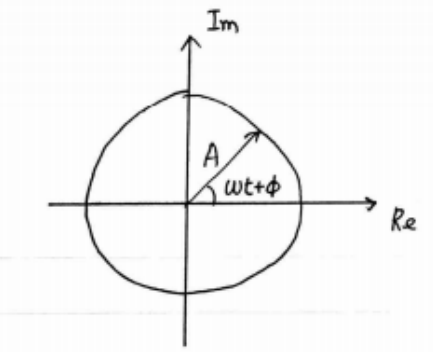
复指数\(e^{i \theta}=\cos \theta+i \sin \theta\)是“Phoenix function”
(1) Cannot be killed by differentiation!!
(2) It has a very nice property: $$ \begin{gathered} e^{i \theta_{1}} \cdot e^{i \theta_{2}}=e^{i\left(\theta_{1}+\theta_{2}\right)} \\ A e^{i(\omega t+\phi)} \frac{t \rightarrow t+a}{\text { Time translation }} A e^{i(\omega(t+a)+\phi)} \end{gathered} $$Time translation is just a rotation in the complex plane!
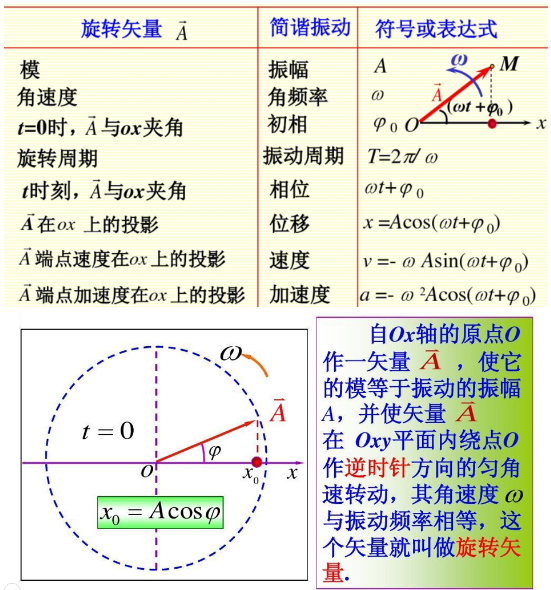 【旋转矢量法】旋转矢量法就是用匀速圆周运动来研究简谐振动中的相位问题或振动时间问题的方法。其优点在于:
【旋转矢量法】旋转矢量法就是用匀速圆周运动来研究简谐振动中的相位问题或振动时间问题的方法。其优点在于:
(1) 直观地表达谐振动的各特征量;
(2) 便于解题,特别是确定初相位;
(3) 便于振动合成。
Damped Free Oscillators
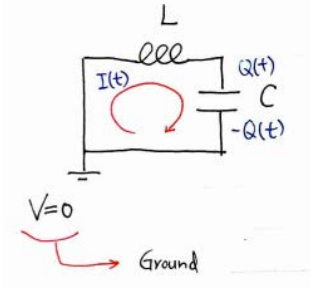
Example: LC Circuit “Coordinate system”: Define clockwise current to be positive.
初始条件:\(t=0 \quad I(0)=I_{\text {Initial }} \quad\) and \(\quad Q(0)=0\)$$ L \frac{d I}{d t}+\frac{Q}{C}=0 \quad \Rightarrow \quad \ddot{Q}+\frac{Q}{L C}=0 $$根据初始条件可以推出通解的余弦项为零,于是最终的解为\(Q(t)=\displaystyle\frac{I_{\text {Initial }}}{\omega_{0}} \sin \omega_{0} t\),其中\(\omega_{0}=\sqrt{\displaystyle\frac{1}{L C}}\)
To compare with our mass and spring system: $$ \begin{array}{ccc} m & \leftrightarrow & L \\ k & \leftrightarrow & 1 / C \\ x & \leftrightarrow & Q \end{array} $$In general, our equation of motion will look like: $$ \mu \frac{d^{2} x}{d t^{2}}=-k x $$Where \(\mu\) is a generalized mass, \(x\) is a generalized coordinate and \(k\) is a generalized spring constant.
“Kinetic energy” \(=\displaystyle\frac{1}{2} \mu\left(\displaystyle\frac{d x}{d t}\right)^{2}\)
"Potential energy" \(=\displaystyle\frac{1}{2} k x^{2}\)
"Total energy" \(\Rightarrow E=\displaystyle\frac{1}{2} \mu\left(\displaystyle\frac{d x}{d t}\right)^{2}+\displaystyle\frac{1}{2} k x^{2}\)
求解\(\ddot{x}+\omega_{0}^{2} x=0\),其中\(\omega_{0}=\sqrt{\displaystyle\frac{k}{\mu}}\),得到$$ \begin{aligned} x(t) &=A \cos \left(\omega_{0} t+\phi\right) \\ \frac{d x(t)}{d t} &=-A \omega_{0} \sin \left(\omega_{0} t+\phi\right) \end{aligned} $$Plugging this into the total energy we get: $$ \begin{aligned} E &=\frac{1}{2} \mu A^{2} \omega_{0}^{2} \sin ^{2}\left(\omega_{0} t+\phi\right)+\frac{1}{2} k A^{2} \cos ^{2}\left(\omega_{0} t+\phi\right) \\ &=\frac{1}{2} k A^{2}\left(\sin ^{2}\left(\omega_{0} t+\phi\right)+\cos ^{2}\left(\omega_{0} t+\phi\right)\right) \\ &=\frac{1}{2} k A^{2} \quad \text { Constant!!! } \end{aligned} $$
 摆杆问题讨论
摆杆问题讨论
初始条件:\(\theta(0)=\theta_{\text {Initial }}\),\(\dot{\theta}(0)=0\)于是$$ \begin{aligned} \vec{\tau} &=\vec{R} \times \vec{F} \\ \tau &=-m g \frac{l}{2} \sin \theta(t) \end{aligned} $$From Newton’s Law:(其中摆杆围绕转动点的转动惯量\(I=\displaystyle\frac{1}{3} m l^2\),角加速度为\(\alpha(t)\))有$$ \tau=I \alpha(t)=I \ddot{\theta}(t)=\frac{-m g l}{2} \sin \theta(t) $$于是角加速度$$ \ddot{\theta}(t)=\frac{-m g l}{2 I} \sin \theta(t)=-\frac{3 g}{2 l} \sin \theta(t) $$为了简化计算,令\(\omega_{0}=\sqrt{\displaystyle\frac{3 g}{2 l}}\),于是得到最终的表达形式$$ \ddot{\theta}=-\omega_0^2 \sin \theta(t) $$However, life is hard! We don’t know how to solve this equation. Not the end of the world. We can either solve it by a computer or we can consider a special case: small angle limit. (The approximation is quite good! )$$ \begin{aligned} \theta(t)=\quad 1^{\circ} & \Rightarrow & \frac{\sin \theta}{\theta} &=99.99 \% \\ 5^{\circ} & \Rightarrow & &=99.9 \% \\ 10^{\circ} & \Rightarrow & &=99.5 \% \end{aligned} $$The equation of motion becomes: $$ \ddot{\theta}(t)=-\omega_{0}^{2} \theta(t) $$We have solved this equation of motion in previous lectures! Recall the solution: \(\theta(t)=A \cos \left(\omega_{0} t+\phi\right)\)带入初始条件很容易解得\( \theta(t)=\theta_{\text {Initial }} \cos \left(\omega_{0} t\right) \)
三种常见的simple harmonic oscillator
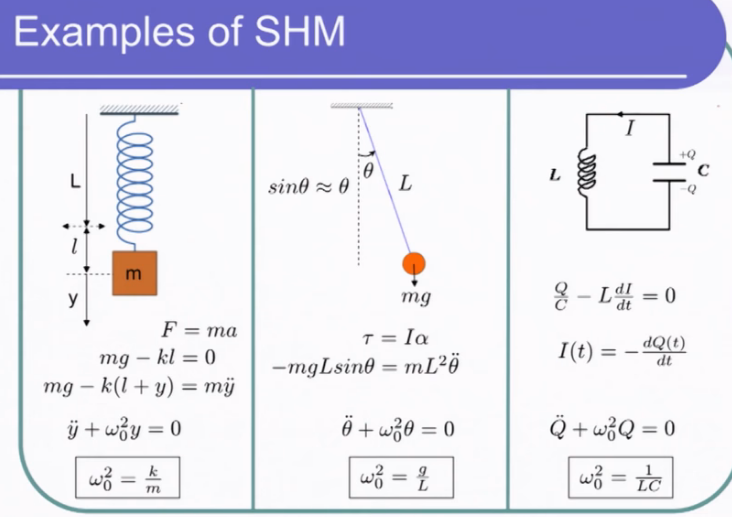
给Free Oscillators增加阻尼项
Now we will add a drag force: $$ \tau_{D R A G}(t)=-b \dot{\theta}(t) $$We chose this form, not only because it is the most realistic but because it is solvable, but also it is not totally unrealistic. If we choose more complicated forms of the drag force, we would have to solve it by a computer.$$\ddot{\theta}(t)=\frac{\tau(t)}{I}=\frac{\tau_{g}(t)+\tau_{D R A G}(t)}{I}=\frac{-m g \frac{l}{2} \sin \theta(t)-b \dot{\theta}(t)}{\frac{1}{3} m l^{2}}$$Implementing the small angle approximation \(\sin \theta(t) \approx \theta(t)\) $$\ddot{\theta}(t)\approx-\frac{3 g}{2 l} \theta(t)-\frac{3 b}{m l^{2}} \dot{\theta}(t)$$Define \(\omega_{0}^{2}=\displaystyle\frac{3 g}{2 l} \quad \Gamma=\displaystyle\frac{3 b}{m l^{2}}\)$$ \ddot{\theta}(t)+\Gamma \dot{\theta}(t)+\omega_{0}^{2} \theta(t)=0 $$Use complex notation! \(\theta(t)=\operatorname{Re}[z(t)]\) Plugging in the trial solution\(z(t)=e^{i \alpha t}\)$$ \begin{aligned} &\ddot{z}(t)+\Gamma \dot{z}(t)+\omega_{0}^{2} z(t)=0 \\ &\left(-\alpha^{2}+i \Gamma \alpha+\omega_{0}^{2}\right) e^{i \alpha t}=0 \end{aligned} $$\(e^{i \alpha t}\) is never zero. Therefore$$\Rightarrow \alpha=\frac{i \Gamma}{2} \pm \sqrt{\omega_{0}^{2}-\frac{\Gamma^{2}}{4}}$$Now there are three possibilities for the last term.
(1) “Underdamped oscillation” where \(\omega_{0}^{2}>\displaystyle\frac{\Gamma^{2}}{4} .\) The drag force is small. 令\(\omega^{2} \equiv \omega_{0}^{2}-\displaystyle\frac{\Gamma^{2}}{4}\),于是得到两个解$$ \begin{aligned} &z_{+}(t)=e^{-\Gamma t / 2} e^{i \omega t} \\ &z_{-}(t)=e^{-\Gamma t / 2} e^{-i \omega t} \end{aligned} $$注意实际数学上的通解是上面两个解的线性组合,线性组合的系数可以是复数,当然了,我们也可以通过这两个解得到两个新的不包含\(i\)的基解\(e^{-\Gamma t / 2} \cos \omega t\)和\(e^{-\Gamma t / 2} \sin \omega t\),它俩的线性组合(组合系数是复数)也是通解\( \theta(t)=e^{-\Gamma t / 2}(a \cos \omega t+b \sin \omega t)\),但是如果对应实际物理过程的话,\(a\)和\(b\)肯定就都只能取实数(\(t=0\)和其一阶导数都是必须是实数)
(2) “Critically damped oscillation” 也就是说\(\omega=0\) No oscillation!
(3) “Overdamped oscillation” which means \(\omega_{0}^{2}<\displaystyle\frac{\Gamma^{2}}{4}\), there is a huge drag force!
注:老师这一部分讲的有点问题,可以参考我的微分方程笔记,或者这里。
Dispersive Medium, Phase Velocity, Group Velocity
信号的传播
我们之前学了机械波,包括声波和电磁波都可以用波动方程来表示:$$\frac{\partial^{2} \psi(x, t)}{\partial t^{2}}=v_{p}^{2} \frac{\partial^{2} \psi(x, t)}{\partial x^{2}}$$我们本节将学习如何用波来传播信息,我们可以传递简谐波(有固定的角频率和波数),但是如果用简谐波传递信息,我们无法知道信息是何时发送的,因为波一直在进行振动。在现实中,我们用脉冲波来传递信息。我们发出一系列的矩形波,之后给接收器设置阈值(虚线),因此我们就可以定义0和1,进而传递信息。(下图的矩形波可以表示为无数多个简谐波的线性叠加)
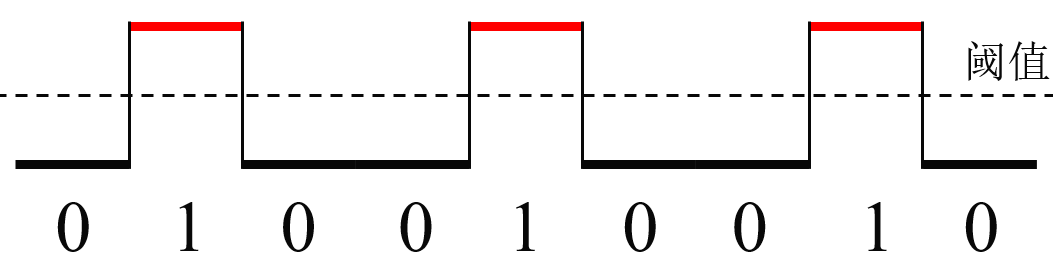
如果此时该波向前传播,即以\(v=\displaystyle\frac{\omega}{k}\)的速度向前传播,如果对于所有的简谐波其\(v\)是相等的,那么我们称这个为【线性色散】关系。那么矩形波在随着时间向前传播的过程中波形不会发生改变,只是再向前传播。如果是【非线性色散】关系,不同波数的波有不同的速度,简谐波的传播速度有快有慢,在向前传播的过程中,波的形状会发生改变。我们下面学来讨论一下非线性关系的成因,并会加以模拟实验。
非线性色散关系对信号的影响
对于简谐振荡\(\displaystyle\frac{\partial^{2} \psi(x, t)}{\partial t^{2}}=v_{p}^{2} \displaystyle\frac{\partial^{2} \psi(x, t)}{\partial x^{2}}\),如果\(v_{p}=\displaystyle\frac{w}{k}=\sqrt{\displaystyle\frac{T}{\rho_{L}}}\),其中\( \rho_{L}\)为density for the unit length,\(T\)为string tension,那么就是线性色散关系,把对应的材料称为【非色散介质】(nondispersive media),因此其色散关系只与\( T \)和\(\rho_{L}\)有关。但是我们在考虑这个体系的时候,我们忽略了一个重要的性质就是【刚度】(Stiffness)。刚度是指材料或结构在受力时抵抗弹性变形的能力。是材料或结构弹性变形难易程度的表征。比如我们对一个钢管进行小幅度的弯曲,在我们放手后钢管会恢复到自己的初始状态,而不会像我们之前讲的系统一样,会生震荡。在考虑刚度以后,它会影响们的弦张力\( T\),因此波方程如下:$$\frac{\partial^{2} \psi(x, t)}{\partial t^{2}}=v_{p}^{2}\left[\frac{\partial^{2} \psi(x, t)}{\partial x^{2}}-\alpha \frac{\partial^{4} \psi(x, t)}{\partial x^{4}}\right]$$其中\(-\alpha \displaystyle\frac{\partial^{4} \psi(x, t)}{\partial x^{4}}\)项为刚度对张力的影响,我们之所以选择四阶导数是因为这和实验测试的结果相对应,并且从物理直觉上,因为刚度应该是左右对称的,即当弯折材料时,左右端会同时恢复,不可能是奇数阶导数。因此我们将我们的简谐波(向\(x\)轴正向传播)的解\(\sin (k x-w t)\)带入微分方程得到$$v=\frac{w}{k}=v_{p} \sqrt{1+\alpha k^{2}}$$此时的色散关系不在是一个常数,而是一个和\(k\)有关的变量。因为不仅张力还有刚度对应的力帮忙将材料恢复到静止,并且波数越大(波长越短),对应的刚度的力越大,于是a lot of dispersion and a higher speed \( v\)。我们可以画一个图来表示该非线性色散关系;另外正是由于散射,我们将会丢失之前矩形波的形状。
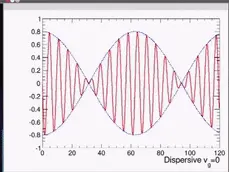
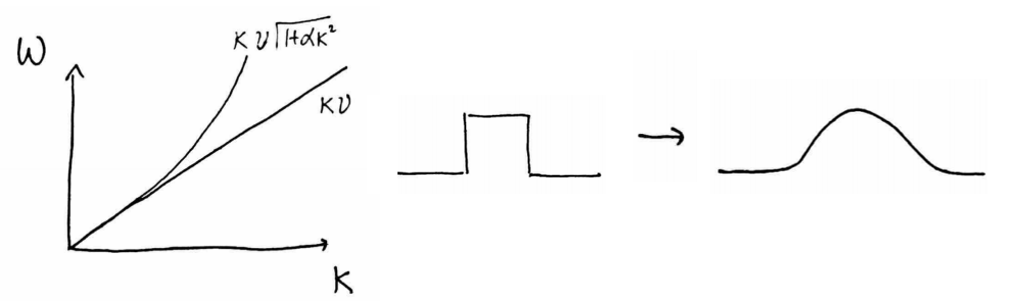 下面的视频是传输三角波,\( \alpha =0.2\)的例子,理想情况下向右传播不会波形的变化,但是由于非线性色散关系的存在,其从左向右传播过程中波形会如红色线所示,主峰发生严重的展宽,并且还伴随着其他的峰的出现。
下面的视频是传输三角波,\( \alpha =0.2\)的例子,理想情况下向右传播不会波形的变化,但是由于非线性色散关系的存在,其从左向右传播过程中波形会如红色线所示,主峰发生严重的展宽,并且还伴随着其他的峰的出现。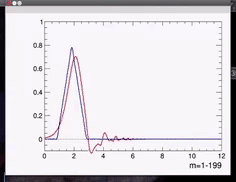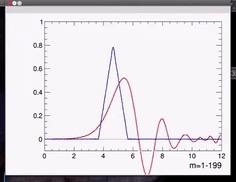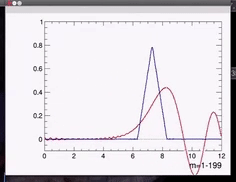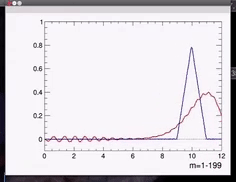
如果这仍然十分难以理解,那么我们只考虑两个简谐波的线性叠加,即【拍频现象】 (Beat Phenomenon)。In acoustics, a beat is an interference pattern between two sounds of slightly different frequencies, perceived as a periodic variation in volume whose rate is the difference of the two frequencies.
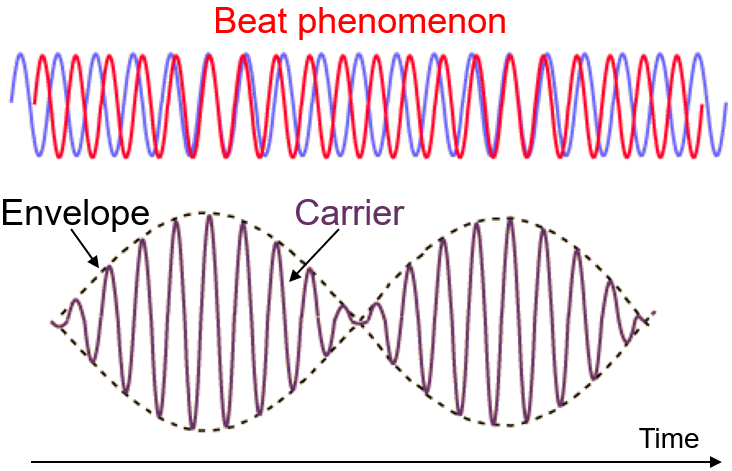
beat frequency稳定:
The composite tone has a frequency of about 238 Hz. The time between minima is about 0.62 seconds, corresponding to a beat frequency of about 1.6 Hz. This implies that the two tones were 1.6 Hz apart in frequency. (参考Beats with two tone generators—hyperphysics)
beat frequency逐渐增大:
![]()
The above sound amplitude trace shows the beat phenomenon as one tone generator is tuned upward in pitch. Click on the player at right to play the sound of the tone generators as one is tuned upward while the other remains at its original pitch.
拍频的数学:两个频率相差不多的波的组合$$\begin{array}{ll} \psi_{1}(x, t)=A \sin \left(k_{1} x-\omega_{1} t\right) & v_{1}=\displaystyle\frac{\omega_{1}}{k_{1}} \\ \psi_{2}(x, t)=A \sin \left(k_{2} x-\omega_{2} t\right) & v_{2}=\displaystyle\frac{\omega_{2}}{k_{2}} \end{array}$$叠加形成的波为$$ \psi(x, t)=\psi_{1}(x, t)+\psi_{2}(x, t)=2 A \sin \left(\frac{k_{1}+k_{2}}{2} x-\frac{w_{1}+w_{2}}{2} t\right) \cos \left(\frac{k_{1}-k_{2}}{2} x-\frac{w_{1}-w_{2}}{2} t\right) $$由于两个波的频率差不多,于是\( k_{1} \approx k_{2} \approx k, w_{1} \approx w_{2} \approx w\),we have amplitude modulation:
我们因此可以定义:
(1) 【相速度】(Phase velocity):\( v_{p}=\displaystyle\frac{w}{k}\),对应carrier 的传播速度,即\(\sin \left(\displaystyle\frac{k_{1}+k_{2}}{2} x-\displaystyle\frac{w_{1}+w_{2}}{2} t\right)\)部分;
注:波是状态的传播,而相位又决定状态,所以波也就是相位的传播,波速就是相速度。(为什么简谐振动是最基本的振动?)
(2) 【群速度】(Group velocity):\(v_{g}=\displaystyle\frac{w_{1}-w_{2}}{k_{1}-k_{2}} \approx \displaystyle\frac{d w}{d k}\),对应envolope的传播速度,即\(\cos \left(\displaystyle\frac{k_{1}-k_{2}}{2} x-\displaystyle\frac{w_{1}-w_{2}}{2} t\right)\)部分。
(3) 【拍频】(beat frequency)如果初始给的两个波的频率分别为\(f_1\)和\(f_2\),那么envolope对应的频率(\( f_{\text{beat}}\))为二者差值的绝对值。$$ f_{\text {beat }}=\left|f_1-f_2\right| $$注意When you say that the beat frequency is \(f_1-f_2\) rather than \((f_1-f_2)/2\), that requires some explanation. For the difference frequency you can just say that you get a minumum when the modulating term reaches zero, which it does twice per cycle, so that the number of minima per second is \(f_1-f_2\).
Carriers and 【Sidebands】(伴带)
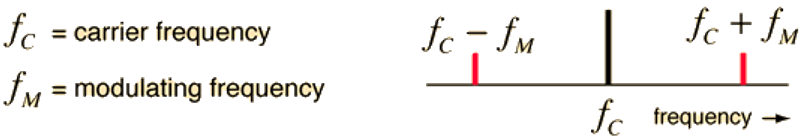 Radio transmission involves putting audio frequency information on a much higher frequency electromagnetic wave called a carrier wave. The process of superimposing the "electrical image" of the sound information on the carrier wave is called modulation, and there are two commonly used schemes: amplitude modulation (AM) and frequency modulation (FM). Either form of modulation produces frequencies which are the sum and the difference of the carrier and modulation frequencies - these frequencies are sometimes called sidebands.
Radio transmission involves putting audio frequency information on a much higher frequency electromagnetic wave called a carrier wave. The process of superimposing the "electrical image" of the sound information on the carrier wave is called modulation, and there are two commonly used schemes: amplitude modulation (AM) and frequency modulation (FM). Either form of modulation produces frequencies which are the sum and the difference of the carrier and modulation frequencies - these frequencies are sometimes called sidebands.
Because of the existence of the sidebands, the frequency range or bandwidth necessary for radio transmission depends on the range of modulating frequencies.

右图示为深水表面的波的传递模式。红色点点以相速度运动,绿色点点以群速度运动。在这个例子中,红点从左向右运动的过程中两次跨过绿点,相速约略为群速的两倍。新的波看起来像是从一个波群的末尾处开始生成,振幅逐渐增大直至到达波群中间,然后再消失于波的前端。对于水表面的重力波,大多数情况下群速度远小于相速度,参考wiki群速度。
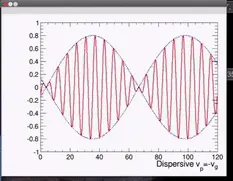
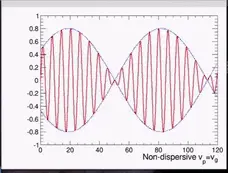 线性介质的中两个频率接近的波叠加传播的示意图如右图$$v_{g}=v_{p}=\text{constant}$$
线性介质的中两个频率接近的波叠加传播的示意图如右图$$v_{g}=v_{p}=\text{constant}$$
不同类型的介质中的色散关系:
(1) 相速度:色散曲线上任一点和原点的连线的斜率就是相速度\( v_p \)
(2) 群速度:色散曲线上任意一点的切线的斜率对应的就是群速度\( v_g \)
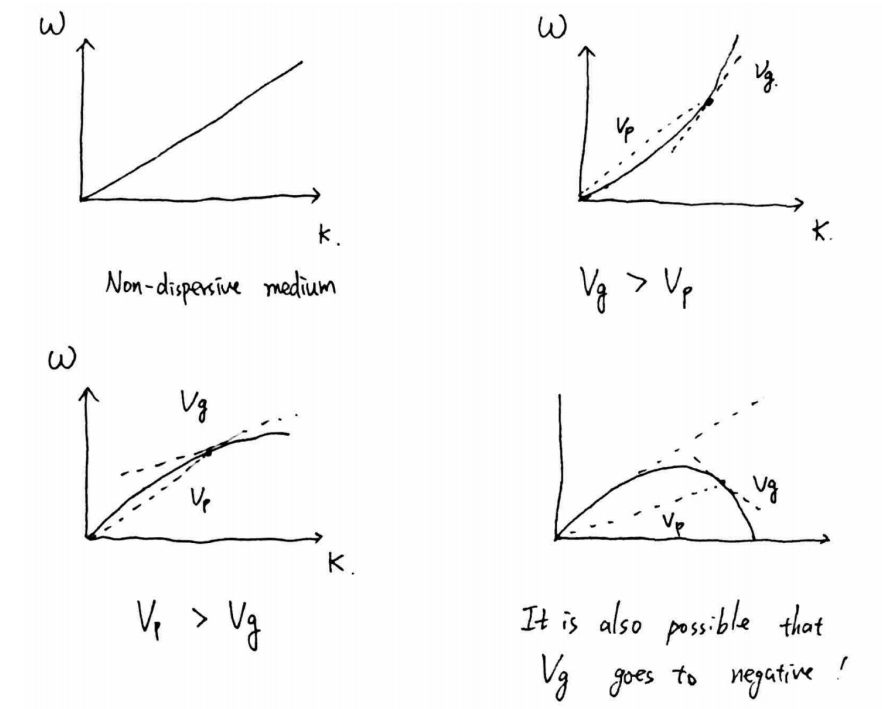
群速度为0的情况:
群速度小于0的情况:
群速度/相速度(李威仪) (来自视频P9)
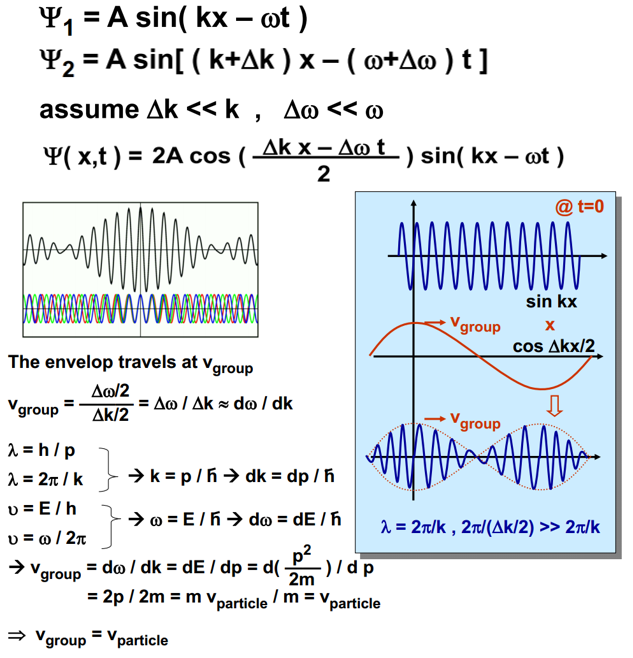
- 波包的行进速度代表粒子的行进速度;
- cos去modulate sin的amplitude;
- 波包振幅的平方,就是粒子出现几率的density;
- 用一个特定的例子,展示了群速度和相速度相等的情况。
参考资料:
(1) 相速度与群速度-动画
(2) 物理_波_拍的现象-PengTitus
光波的叠加
参考:ppt
李永乐相关合集
WIFI和微波炉加热食物会对人有害吗?致癌吗?李永乐老师讲微波炉原理
拓展参考《微波加热技术的应用与研究进展-2003》
- 微波波长:1-1000 mm
- 微波加热的原理:当有极分子电介质和无极分子电介质置于微波电磁场中时,介质材料中会形成偶极子或已有的偶极子重新排列,并随着高频交变电磁场以每秒高达数亿次的速度摆动,分子要随着不断变化的高频电场的方向重新排列,就必须克服分子原有的热运动和分子相互间作用的干扰和阻碍,产生类似于摩擦的作用,实现分子水平的“搅拌”,从而产生大量的热可见常规加热与微波加热是两种迥然不同的加热方法微波加热是一种“冷热源”,它在产生和接触到物体时,不是一股热气,而是电磁能它具有一系列传统加热所不具备的独特优点。
- 微波加热的特点:
- 即时性:只要有微波辐射,物料即刻得到加热反之,物料就得不到微波能量而立即停止加热。
- 整体性:一种穿透力强的电磁波,其加热过程在整个物体内同时进行。
- 选择性:材料分为微波反射型、微波透明型、微波吸收型和部分微波吸收型,因此,我们可以利用微波加热的选择性对混合物料中的各组分或零件的不同部位进行选择性加热(比如胶合加工,只加热胶层)。
- 高效性
- 环保、杀菌:没有通过化石能源燃烧加热这种低效的方式,用微波辐射生物体时,除了产生微波热效应外,微波还能使生物体的生物活性得到抑制或激励,即微波的非热效应或生物效应。
- 应用:
- 微波加热与解冻
- 微波干燥:微波干燥是把固体湿物料作为一种电介质,置于微波交变电磁场中,在频繁交变电磁场的作用下,物料中的极化水分子迅速旋转,相互摩擦,产生热量,从而加热和干燥物料!用微波对物料进行干燥时,一般物料表面温度低于芯层温度,形成“负温度 场”(一般加热方式为正温度场),且物料内产生较高的蒸汽压力,与环境形成较大的静压力差,使物料中的自由水和水蒸气形成渗透流!负温度场和物料内外静压力梯度的存在,使微波干燥完全不同于传统的物料干燥方法,形成了微波干燥的独特机理!它具有干燥速度快、质量好的优点。
- 微波烧结:材料内部结晶结构更加均匀,致密度更高,改善了材料的性能;实现选择性烧结,产生具有新的微观结构和优良性能的材料。大幅度缩短烧结时间和节约电能的优点。
- 微波杀虫、灭菌:很多研究表明:当物料作用于微波场中时,能引起物料的温升,即产生“温度场”,同时,还能造就“电磁场”,对生物体产生比温度场更大的效能,即微波的生物效应,从而达到杀虫、灭菌的目的,但有些学者认为,微波的量子能量远低于H-OH的弱化学结合能,因此用微波的非热效应达到杀虫、灭菌的目的是不可能的,其影响生物体的只能是微波的热效应。
广播信号传输FM/AM
信号发射和接收:我们首先需要知道,要想把一个信号传输出去,那么这个信号必须是高频信号,低频穿不远。一般声音和图像都是低频信号,我们必须把它们变成高频信号,这个过程就成为调制。
那么为什么无线电通信要将低频信号调制到高频传输呢?基带信号频率低,波长长,当天线的长度为无线电信号波长的1/4时,天线的发射和接收转换效率最高,如果不调制到高频,天线需要做得很长;空间中的频谱资源是有限的,每个信道都严格划分给固定用途,通过载波调制可以选择合适的信道进行传输;高频要比低频传送的成本低效率高。利用高频的不同的载波,容易实现多路通信。
(1)调制
调幅(AM)和调频(FM),幅度就是amplitude,频率就是frequency。李永乐形象比喻,我们要传输的信息就是“蛋糕”,但是不能直接快递蛋糕,需要把蛋糕装到“盒子”里面,这个盒子就是高频信号,最后得到的装有蛋糕的盒子可以是AM,也可以是FM。
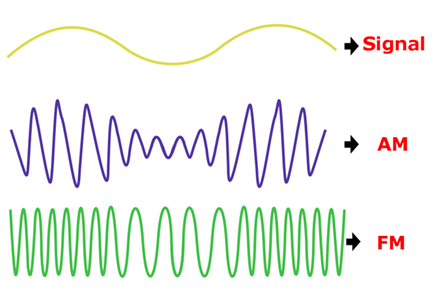
AM是中波,可以被大气层反射,可以通过衍射绕开障碍物,传播距离远,通常做为省际电台使用。
FM是短波,学过高中物理的同学可能还记得,短波直线传播性能好,但是躲不开障碍物,所以FM只适合做短距离传播,所以我们通常听到的FM也都是地方城市电台。
通常我们听到的AM电台,声音都是品质比较低的,稀里哗啦的,因为AM采用的是中波段。频率比较低一般在1000KHz上下,每一秒能传递的0101的信息量比较少,所以声音就比较失真。而FM通常在100Mhz左右,是AM的100倍,所以FM音质更好,还能支持双声道立体声。
(2)信号的发射
信号源,连接一个电感,然后通过电感耦合,左边电感磁通量的变化导致右边(右边整体是个天线)的也变化,于是右边的电路就产生振荡电流,最终形成电磁波发射出去。
(3)信号的传播
(A)直射波:波长短、频率高的波(微波),绕射能力差,不能沿着弯曲的地球表面传播,所以传播距离短,需要每隔几十千米设立中继站(类似接力赛跑)。当然,有了同步卫星,这一切就变得更简单。
(B)天波:短波被地面吸收得多,但能较好地被电离层反射,所以主要靠天波传播。
(C)地波:长波和中波,绕射能力强,很好地绕开障碍物,所以可以沿着弯曲的地球表面传播,传播距离长。
中波和中短波在夜晚被电离层吸收得不多,可以靠天波传播,在白天仍靠地波传播,但地面对它们的吸收较强,不能传得很远,这就是人们在晚上能收听到较多外地电台广播的原因。(参考无线电波的传播途径)
(4)信号的接收
电感的特点是:希望维持电流不变,通低频,阻高频。
电容的特点:通高频,阻低频。
这里左边的LC电路有一个固有频率(谐振频率),当然实际中是不存在没有电阻的电路的,总而言之,我们可以把这个看作是RLC电路中电阻为0的情况,关于RLC电路,我们在MIT电和磁里面有详述,谐振频率和R无关,为\( f=\displaystyle\frac{1}{2 \pi \sqrt{L C}}\)。通过改变电容大小,来改变谐振频率,来把我们需要的信号频率摘出来,这一过程叫作“调谐”。
(5)解调
通过互感,将电信号转到另外一个电路上。右边的就是一个检波电路,用到了二极管,真空二极管发明之初就是用于检波电路。(相当于把快递给拆了,拿出真正的蛋糕)
参考资料:
(1) 李永乐视频
(2) 珂学原理:比如人正常说话的频率为500~3000HZ,那么根据光速等于波长乘以频率,那么3000HZ的至少需要100000米长的天线,500HZ的至少需要600000米的天线。这在工程实践中,是不可能的。低频容易被云、雾霾干扰。解决的办法是:频率提高,同时保留信息,这就要调制,包含调幅、调频、调相。
(3) 为什么无线电通信要将低频信号调制到高频传输?