化学学习的相关网站-图床：chemistry-img/

ChemTube3D
Chemistry-Psiberg
Chemguide—Helping you to understand Chemistry
Chemistry Learner
PhET Interactive Simulations
Organic Chemistry Resources and Study Tips
上海交通大学-普通物理
黄建滨-北京大学
《现代物理有机化学》-笔记
基础有机化学(邢其毅)--史上最好的PPT课件
有机化学结构图谱全解
mathpix+smiles code + chemdraw

有机化学

有机化学入门章节

【共轭效应】(conjugated effect)：又称离域效应，是指共轭体系中由于原子间的相互影响而使体系内的\(π \)电子(或\(p\)电子)分布发生变化的一种电子效应。共轭体系中的电子云是离域的而不是定域的，使得所涉及到的化学键平均化，这种在共轭体系中原子之间的相互影响的电子效应叫共轭效应。

类型：

• \(π \)-\(π \)共轭体系
• \(p\)-\(π \)共轭体系
• 超共轭体系：
  • \(σ\)-\(π \)共轭
  • \(σ\)-\(p\)共轭

诱导效应

生色团

助色团

参考：
(1) 诱导效应和共轭效应 
(2) 暨南大学药学院考研～共轭体系及共轭效应

 

 

SN1 和SN2  补充

 

推广应用

卡宾

参考资料：
(1) 【大家】Steven P. Nolan——NHC-金属有机配合物
(2) 卡宾(维基百科)

 

原子结构和分子结构

范德华力

The van der Waals force is a distance-dependent interaction between atoms or molecules. Unlike ionic or covalent bonds, these attractions do not result from a chemical electronic bond;[2] they are comparatively weak and therefore more susceptible to disturbance. The van der Waals force quickly vanishes at longer distances between interacting molecules.

范德华力包含：Keesom Forces, Debye Forces, London Dispersive Forces.

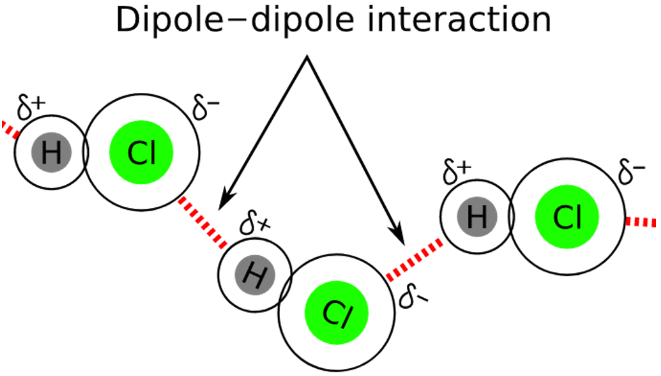【Keesom Forces】: Keesom forces are the temperature dependent and very weak van der Waals forces that originate between permanent dipoles. As, molecules rotate constantly and it is generally assumed that they cannot be locked in one place, but at some points, they do get locked. These interactions arise at those moments and are seen in all quadrupoles and multipoles. Keesom forces are named after William Hendrik Keesom and arise due to interactions between permanent polar structures.

【德拜力】(Debye Forces): The intermolecular force of attraction that exists between a permanent dipole and another dipole induced by the first one. So the Debye force can also be called permanent dipole-induced dipole interaction.

Debye force is only attractive and does not disappear at higher temperatures. It cannot occur between atoms, unlike the London dispersion force.

例子：
(1) Argon molecule experiences dipolar characteristics when attracted by the hydrogen atom of HCl or repelled by the chlorine atom of HCl.
(2) Polar molecules such as water, create dipoles in neutral molecules like oxygen, etc.

【伦敦色散力】(London Dispersive Forces): Also known as the “temporary dipole-induced dipole”, “instantaneous dipole-induced dipoles”, or “fluctuating dipole-induced dipole". The electron distribution around an atom or molecule undergoes fluctuations in time. These fluctuations create instantaneous electric fields which are felt by other nearby atoms and molecules, which in turn adjust the spatial distribution of their own electrons. The net effect is that the fluctuations in electron positions in one atom induce a corresponding redistribution of electrons in other atoms, such that the electron motions become correlated. 总而言之就是形成instantaneous dipoles attract each other. 更深层次的原因需要用量子力学来解释。

例子：F₂、Cl₂、Br₂、I₂、He、Ar、O₂、N₂、CO₂、CH₄、CCl₄。

伦敦色散力的性质：

• Forces are attractive
• Forces are present between all atoms – polar and nonpolar
• Larger atoms display stronger forces than smaller ones, i.e., the strength increases down a particular group in the periodic table
• Easily polarizable atoms and molecules have stronger forces than harder polarizable ones
• Cylindrically shaped molecules allow more molecules to come close to one another than spherical ones, thereby increasing their strength

wiki的描述：科学家观察到在高压低温下，即使是非极性分子也能被液化或固化，弗里兹·伦敦认为非极性分子间必然有吸引力存在，否则在任何条件下非极性分子在任何条件下应该都是气体，此吸引力即为伦敦色散力。 其能量很小，存在所有分子之间。非极性分子内的电子云运动会造成瞬间分布不均匀，产生瞬间偶极，此瞬间偶极又会使附近的非极性分子产生暂时的诱发偶极现象并且是在低概率的可能性中发生的，使非极性分子互相吸引，此种作用力又称瞬间偶极-诱发偶极力。

对比：

	Dipole-dipole Forces	London Dispersion Forces
Definition	Occurs between two polar molecules	Occurs due to the presence of temporary dipole moments caused by moving electrons
Strength	Stronger than dispersion forces	Weaker than dipole forces
Polarity	Permanent	Temporary
Examples	HCl, H2O, and acetone	He, Cl2, and CCl4

参考资料：
(1) London Dispersion Forces—chemistrylearner
(2) Intermolecular forces: Types, Explanation, Examples

 

多电子原子轨道能级

(1) Pauling近似能级图(高中老师讲的部分)

“能级分裂”：主量子数\(n\)相同，角量子数\(l\)不同的能级，能量随\(l\)的增大而升高。
“能级交错”：当主量子数\( n\)和角量子数\( l\)均不同时，出现能级交错现象，比如\( E_{4 s}<E_{3 d}<E_{4 p} \cdots\)。

(2) Cotton能级图

在Pauling近似能级图之后，人们注意到原子轨道的能量和原子序数有关，提出了新的能级图，Cotton能级图便是其中的一种，它概括了理论和实验的结果，定性地表明了原子序数改变时，原子轨道能量的相对变化。

• 反映出主量子数相同的氢原子轨道的简并性。对氢元素来说，其主量子数相同的各轨道全处于同一能量点上，即不存在能级分裂现象。
• 反映出原子轨道的能量随着原子序数的增大而降低。
• 反映出随着原子序数的增大，原子轨道能级下降幅度不同，因此能级曲线产生了相交现象。例如\(3d\)和\(4s\)轨道的能量高低关系：K，Ca的\(E_{3 d}>E_{4 s}\)；而原子序数较小或较大时，\(E_{3 d}<E_{4 s}\)。

(3) 屏蔽效应

He原子核内含有2个质子，描述He原子的能量状态，不仅要考虑原子核对外层电子的吸引能和外层电子自身的动能，还要考虑两个电子之间的排斥能。He原子的薛定谔方程难解的根源是排斥能的存在，从而难以精确地说明一个电子对另一个电子的影响。解决的办法就是用近似处理法。我们可以认为，He原子中的一个电子对另一个电子产生了电荷屏蔽，即削弱了核电荷对该电子的吸引力。于是有效核电荷数\(Z^{*}=2-\sigma\)，其中\(\sigma\)为核电荷的减小值，称为屏蔽常数。

上述近似处理方法是建立在中心势场模型基础上，认为每个电子都是在原子核和其余电子所构成的平均势场中运动，借此，可以使多电子薛定谔方程分离成一组单电子方程，然后求解。一般来说，内层电子对外层电子的屏蔽作用较大，同层电子的屏蔽作用较小，外层电子对较内层电子可以近似地看作不产生屏蔽作用。

(4) 钻穿效应

照理说，能量越大的电子分布离原子核越远，但是电子具有波动性，电子可以在原子区域的任何位置出现，也就是说，最外层电子有时也会出现在离核很近处，只是概率较小而已。在原子核附近出现概率较大的电子，可以更多地避免其余电子的屏蔽，受到核的较强吸引而更靠近核，这种进入原子内部空间的作用叫作“钻穿效应”。当主量子数\(n\)相同时，角量子数\(l\)越小的电子，钻穿效应越明显，能级也越低。

核外电子排布

(1) 基态原子的核外电子排布原则

人们根据原子光谱实验和量子力学理论，总结出三个排布原则：

• 能量最低原理，电子在原子轨道中的排布，要尽可能使整个原子系统能量最低。
• Pauli不相容原理，同一原子轨道最多容纳两个自旋方式相反的电子，或者说同一原子中不能有一组四个量子数完全相同的电子。
• Hund规则，在相同\( n\)和相同\(l\)的轨道上分布的电子，将尽可能分占\(m\)不同的轨道，且自旋平行。

能量相同的等价原子轨道(或简并轨道)，在全充满(\(\mathrm{p}^{6}, \mathrm{~d}^{10}, \mathrm{f}^{14} \))、半充满(\(\mathrm{p}^{3}, \mathrm{~d}^{5}, \mathrm{f}^{7}\))、以及全空(\(\mathrm{p}^{0}, \mathrm{~d}^{0}, \mathrm{f}^{0}\))的情况下，原子处于比较稳定的状态。

(2) 基态原子的核外电子排布

两种记忆方法，一种是按照高中老师教的画出来。另一种是出现d轨道时，电子按照ns，(n-1)d，np的顺序在原子轨道上排布；若d轨道与f轨道均已出现时，电子按照ns，(n-2)f，(n-1)d，np的顺序在原子轨道上排布。这是一般规律，适用于大多数基态原子的核外电子排布。

       Cr和Cu原子的原子序数分别为24和29，其原子的电子排布分别为\([\mathrm{Ar}] 3 \mathrm{~d}^{5} 4 \mathrm{~s}^{3}\)和\([\mathrm{Ar}]  3 d^{10} 4 s^{1}\)，而不是\([\mathrm{Ar}]  3 d^{4} 4 s^{2}\)和\([\mathrm{Ar}] 3 \mathrm{~d}^{9} 4 \mathrm{~s}^{2} \)，因为半充满和全充满结构是能量较低的稳定结构。

元素性质的周期性

差一张图

(1) 原子半径
依据量子力学的观点，电子在核外运动没有固定的轨道，只是概率分布不同，因此，原子没有明确的界面，不存在经典意义上的半径。人们假定原子呈球体，借助相邻原子的核间距来确定原子半径。基于此假定以及原子的不同存在形式，原子半径可以分为金属半径、共价半径和范德瓦尔斯半径。

• 金属半径：金属单质晶体中，两个最近邻金属原子核间距的一半。
• 共价半径：同种元素的两个原子以共价单键结合时，其核间距的一半。
• 范德华尔斯半径：分子晶体是以范德华尔斯力结合的，比如稀有气体形成的单原子分子晶体中，两个同种原子核间距的一半。

同一周期中，原子半径的大小受两个因素的制约：

•  随着核电荷的增加，原子核对外层电子的吸引力增强，使原子半径逐渐变小；
• 随着核外电子数的增加，电子间的斥力增强，使原子半径变大。
  由于前者的作用比后者更显著，即增加的电子不足以完全屏蔽所增加的核电荷，所以从左向右，有效核电荷逐渐增大，原子半径逐渐变小。

待补充

(2) 电离能 (Ionization Energy)

基态气体原子失去电子成为带一个正电荷的气态正离子所需的能量称为“第一电离能”，由+1价气态正离子失去电子称为+2价气态正离子所需的能量教第二电离能，以此类推。随着原子逐步失去电子所形成的离子正电荷数越来越多，失去电子变得越来越难。通常讲的电离能，如果不特别注明，一般默认是第一电离能。

电离能的大小反映了原子失去电子的难易。电离能越小，原子失去电子越易，金属性越强；反之，电离能越大，原子失去电子越难，金属性越弱。电离能的大小主要取决于原子的有效核电荷、原子半径和原子的电子层结构。

• 同一周期，从碱金属到卤素，元素的有效核电荷逐个增加，原子半径逐个减小，电离能逐个增大。第一主族的最小，稀有气体的最大。
• 长周期的中部元素(即过渡元素)，由于电子加到次外层(ns，(n-1)d，np或者ns，(n-2)f，(n-1)d，np)，有效核电荷增加不多，原子半径减小缓慢，电离能仅略有增加。
• N，P和As等的电离能较大，Be和Mg的电离能也较大，均比它们后面的元素的电离能大，这是半满和全满状态，比较稳定，失去电子相对较难。
• 同一族从上到下，最外层电子书相同，有效核电荷增加不多，原子半径的增大成为主要因素，致使核对外层电子的引力依次减弱，电子逐渐易于失去，电离能依次减小。
• 电离势(ionization potential)和电离能是同一个意思，但是前者是an older and obsolete term。

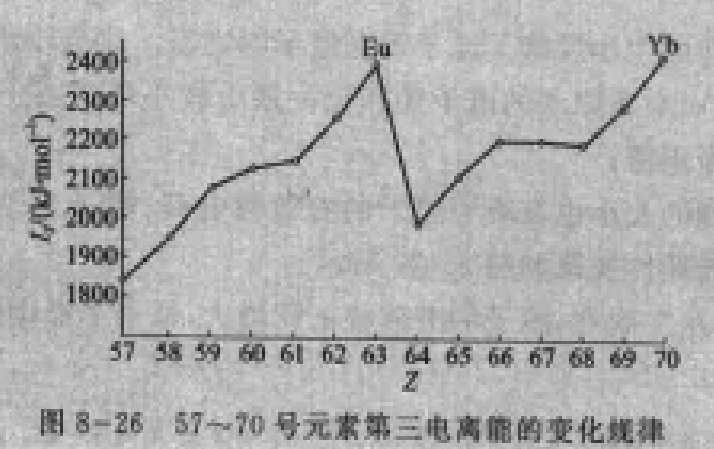
(3) 电子亲和能(Electron Affinity)

元素的气态原子在基态时获得一个电子成为-1价气态负离子所放出的能量称为电子亲和能。如果不加以注明，都是指第一电子亲和能。当-1价离子获得电子时，要克服负电荷之间的排斥力，因此要吸收能量。

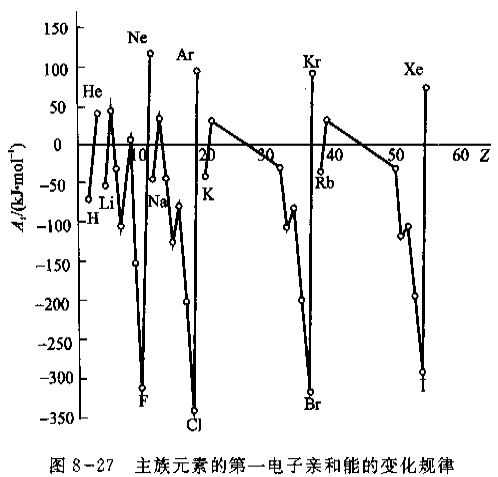
• 电子亲和能的大小反映了原子得到电子的难易。非金属原子的第一电子亲和能总是负值，而金属原子的电子亲和能一般为较小负值或正值。稀有气体的电子亲和能均为正值。
• 电子亲和能的大小也取决于原子的有效核电荷、原子半径和原子的电子层结构。
• 同一周期，从左到右，原子的有效核电荷增大，原子半径逐渐减小，同时由于最外层电子数逐渐增多，趋向于结合电子形成8电子稳定结构。元素的电子亲和能的负值在增大。卤素的电子亲和能呈现最大负值。
• 碱土金属因为半径大，且有\(n \mathrm{~s}^{2}\)电子层结构难以结合电子，电子亲和能为正值。
• 稀有气体具有8电子稳定构型，更难以结合电子，因此电子亲和能为最大正值。
• N原子比较特殊，电子亲和能是正值，是p区元素中除稀有气体外唯一的正值，这是由于它具有半满p亚层稳定电子构型，加之原子半径小，电子间斥力大，得电子困难。
• Cl原子的电子亲和能的负值最大，而不是F原子，这可能是由于F原子的半径小，进入的电子受到原有电子较强的排斥，用于克服电子排斥所消耗的能量相对多一些。

注：
(1) 注意国内外对电子亲和能的正负值是相反的，参考这里，wiki上的正负值和上图相反，和IUPAC Gold Book一致。大多数情况下体系放出能量应该取负值，但是习惯上(IUPAC)电子亲和能正好相反，取正值说明体系放出能量。
(2) Eu²⁺-Tb³⁺的pair的基态比Eu³⁺-Tb²⁺的基态低。

(4) 电负性

电离能和电子亲和能分别从一个侧面反映了原子失去电子和得到电子的难易程度。为了比较分子中原子间争夺电子的能力，对上述两者需要统一考虑，引入了元素电负性的概率。电负性概念的解释是一个分子中的一个原子对于内部成键电子的相对吸引力，而不是分子对于外部自由电子的吸附作用。

        电负性是原子在分子中吸引电子的能力，不是一个孤立原子的性质，而是在周围原子影响下的分子中原子的性质。为了比较不同原子的电负性，Pauling最早建立了电负性标度，他把氢的电负性指定为2.2的基础上，基于相关分子的键能数据，与H的电负性对比，得到其他元素的电负性值，因此个元素原子的电负性是相对数值。

        Pauling电负性标度\(\chi_{\mathrm{P}}\)是目前广泛使用的一种，电负性标度有多种，数据各有不同，但在周期系中电负性变化规律是一致的。电负性可以综合衡量各种元素的金属性和非金属性。Pauling电负性标度中，金属元素的电负性一般在2.0以下，之上为非金属元素。同一周期，从左到右电负性依次增大，元素的非金属性增强，金属性减弱；同一主族，从上到下，电负性依次变小，元素的非金属性减弱，金属性增强。过渡元素的电负性递变不明显，它们都是金属，但金属性都不及第一和第二主族元素。

参考资料：
(1)  中山大学无机化学复习
(2) 核外电子排布和元素周期律

Lewis理论

为了说明像H₂和CCl₄这样的分子是怎样形成的，1916年美国化学家路易斯提出了电子对键理论，他认为这个像两个分子是通过原子之间共用电子对而形成的。通常，电负性相同或者差值很小的非金属元素原子形成的化学键为共价键，两个原子之间必须共用电子，即电子配对才能形成共价键，故简称为“电子配对理论”。在分子中，每个原子均应具有稳定的稀有气体原子的8电子外层电子构型(He除外)，习惯上称为“八隅体规则”。

存在的问题或缺陷
(1) 存在电荷排斥的两个电子为何能以共用电子对的形式将两个原子结合在一起，Lewis理论无法给以说明。
(2) Lewis结构式并不代表分子形状，而仅仅代表成键方式和键的数目。
(3) 存在相当数量不符合“八隅体规则”的例子，比如BF₃，PCl₅和SF₆这些稳定分子。

(1) BF₃， 三氟化硼气体刺激性强，加热或与湿空气接触会分解形成有毒和腐蚀性的氟化氢气体，腐蚀眼睛、呼吸道和皮肤。高纯三氟化硼三氟化硼常用于半导体集成电路生产的掺杂、离子注入等工艺中。
(2) PCl₅可用于六氟磷酸锂(电解液的重要组成)的制备
\(\quad \quad \quad \quad \quad \mathrm{PCl}_{5}+6 \mathrm{LiF} \rightarrow \mathrm{LiPF}_{6}+5 \mathrm{LiCl}\)
(2-a) 湿法：该方法是将锂盐溶于无水氢氟酸中形成LiF·HF溶液，然后通入PF₅气体进行反应生产六氟磷酸锂结晶。经分离，干燥得到产品。
(2-b) 干法：该方法是将LiF用无水HF处理，形成多孔LiF，然后通入PF₅气体进行反应，从而得到产品。
(3) SF₆，根据VSEPR理论它是nonploar分子，the fluorine atom is higher electronegative than sulfur atom due to which the fluorine atom attracts the bonded pair of electron slightly towards itself. As a result, the S-F bond becomes polar and results in a dipole moment but due to symmetry, the dipoles get canceled out with each other making the SF₆ a nonpolar molecule.[reference]

SF₆ is used in the electrical industry as a gaseous dielectric medium for high-voltage sulfur hexafluoride circuit breakers, switchgear, and other electrical equipment, often replacing oil-filled circuit breakers (OCBs) that can contain harmful polychlorinated biphenyls (PCBs). [wiki]

价键理论

量子力学应用于求解氢分子，成功揭示了共价键的本质，由此推广到其他分子系统，发展成为价键理论。

基本要点：
(1) 原子中自旋方向相反的未成对电子相互接近时，可以相互配对形成稳定的化学键。一个原子有几个未成对电子，就可以与几个自旋相反的未成对电子配对成键。
(2) 形成共价键时，成键电子的原子轨道必须在对称性一致的前提下发生重叠，原子轨道的重叠程度越大，两核间电子的概率密度就越大，形成的共价键就越稳定。

共价键的特点：
(1) 共价键具有饱和性。
(2) 共价键具有方向性。除了s轨道外，p、d和f轨道在空间都有一定的伸展方向，成键的时候只有沿着一定的方向取向，才能满足最大重叠原则。

共价键的基本类型：
【\(σ\)键】：由两个相同或不相同的原子轨道沿轨道对称轴方向相互重叠而形成的共价键，叫做\(σ\)键。共价单键是\(σ\)键，共价双键有一个\(σ\)键，\(π \)键，共价三键由一个\(σ\)键，两个\(π \)键组成。
(1) \(σ\)键有方向性，两个成键原子必须沿着对称轴方向接近，才能达到最大重叠。
(2) 成键电子云沿键轴对称分布，两端的原子可以沿轴自由旋转而不改变电子云密度的分布。
(3) \(σ\)键是头碰头的重叠，与其它键相比，重叠程度大，键能大，因此，化学性质稳定。

【\(π \)键】：在化学上是共价键的一种。当两个电子轨道的突出部分发生重叠时产生。名字中的希腊字母\(π \)代表了p轨道，因为\(π \)键的轨道对称性与轨道相同。p轨道通常参与形成\(π \)键，然而，d轨道同样能参与形成。 \(π \)键通常比\(σ\)键弱，因为它的电子云距离带正电的原子核的距离更远，需要更多的能量。由一个\(σ\)键和一个\(π \)键组成的C=C双键的键能小于C-C单键的两倍,表明\(π \)键所增加的稳定性小于\(σ\)键的稳定性。量子力学的观点认为，键的强度很弱主要是因为平行的p轨道间重叠不足。这与\(σ\)键形成对比，\(σ\)键直接在键合原子的核之间形成键合轨道，使得有更大的重叠区,所以\(σ\)键的强度也更强。

对比：\(σ\)键的电子云密度集中在键轴上，\(π \)键的电子云密度集中在键轴的上下方。

【配位键】：共用的一对电子由一个原子单独提供的共价键叫作配位键，用箭头而不用短线表示，以示区别。一个有空轨道，一个有孤对电子。
例子：CO，NH₄⁺，HBF₄，[Cu(NH₃)₄]²⁺，有人认为硝酸和硫酸也有配位键。

The possible coordination geometries around copper in Cu(NH3)42+ span a continuum from square planar to tetrahedral. Square planar coordination produces a much larger gap between the d orbitals of the complex than does tetrahedral coordination. The color of the complex arises from excitation of an electron from one d orbital to a higher energy d orbital. Given this fact, and the fact that most d-d electronic transitions occur in the visible region, which coordination geometry (tetrahedral or square planar) do you think is more likely for Cu(NH3)42+? Provide a brief rationale for your answer. Note: the color of the complex arises from light that is not absorbed.

 

杂化轨道理论

 

 

分子轨道理论

Lewis的电子对成键理论直观、简明，价键理论教好地说明了共价键的行程，为引入量子力写处理分子结构奠定了基础。但是该理论把行程共价键的电子只定域在两个相邻原子之间，没有考虑整个分子的情况，因此不能解释某些分子的性质：
(1) O₂分子有顺磁性，表明含有未成对电子，但是其路易斯结构式电子都成对了；
(2) H₂⁺和He₂⁺的形成；
(3) B₂H₆等缺电子化合物，价键理论无法解释；
(4) 无法解释物质的颜色。

于是20世纪20年代末，人们提出了分子轨道理论，建立了分子的离域电子模型。分子轨道理论与价键理论称为量子力学理论描述分子结构的两大不同分支，但是分子轨道理论比价键理论发展更为广泛，在药物设计等领域都得到了重要应用。

理论要点：
(1) 在分子中的电子不局限在某个原子轨道上运动，而是在分子轨道上运动。分子中每个电子的运动状态可以用波函数\( \psi \)来描述，此\(\psi  \)称为【分子轨道】。
(2) 分子轨道可以由组成分子的原子的原子轨道线性组合而成。例如，原子A和B的原子轨道波函数分别为\(\psi_A\)和\(\psi_B\)，它们线性组合成两个分子轨道：$$\begin{aligned} \phi_{1} &=C_{1} \psi_{\text {A }}+C_{2} \psi_{\mathrm{B}} \\ \phi_{2} &=C_{1} \psi_{\mathrm{A}}-C_{2} \psi_{\mathrm{B}} \end{aligned}$$(a) 组合形成的分子轨道与组合前的原子轨道数目相等，但是能量不同。
(b) \( \phi_{1}\)是能量低于原子轨道的成键分子轨道，是原子轨道同号重叠(波函数相加)形成的，电子出现在核间区域概率密度大，对两个核产生强烈的吸引作用，形成的键强度大。反之\( \phi_{2}\)，波函数异号，电子密度减小，不利于成键。
(c) 【节面】就是波函数位相正负号发生改变的地方(要么平行于键轴，要么垂直于键轴，该处的电子云密度为零)。\(π \)分子轨道有通过键轴(原子核的连线)的节面，而\(σ\)分子轨道没有通过键轴的节面。

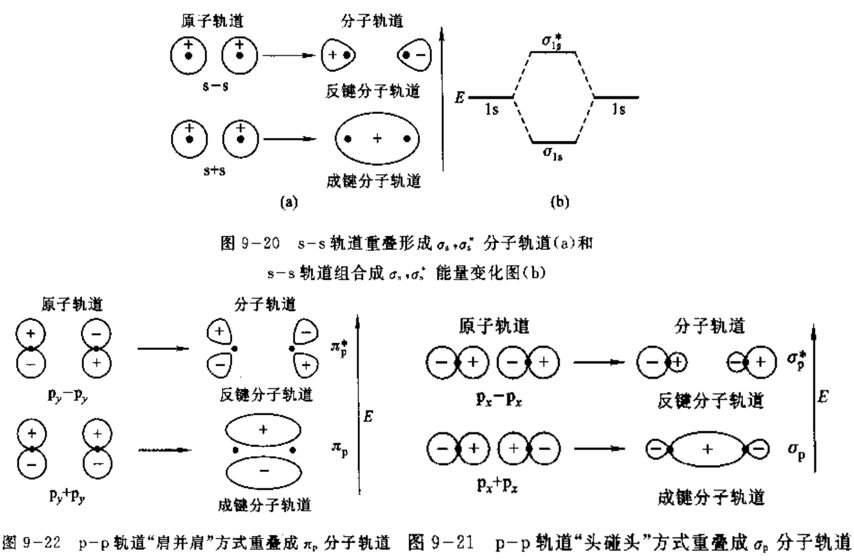
右上角有星号，表示【反键轨道】，没有星号则表示【成键轨道】；右上角的数字表示该分子轨道中的电子个数。

原子轨道线性组合要遵循的原则：
(1) 原子轨道倾向于与能量相近的其他原子轨道结合；
(2) 两个原子轨道的重合部分越多，形成的成键分子轨道能量越低，反键分子轨道能量越高，即分裂能越大；
(3) 每一个分子轨道最多可以容纳一对自旋方向相反的电子；
(4) 如有两个能量相同的分子轨道，电子的排布遵循洪特规则(即如有两个电子，则各自分布在两个轨道中，且自旋方向相同)。

分子轨道法：碳碳双键中\(\pi\)键的形成

在分子轨道理论中，共价键的强度用【键级】来定义：
键级 = (成键轨道电子数-反键轨道电子数)/2
在价键理论中，键级如果为1，则表示单键；如果为2，则表示双键。但是，分子轨道键级也可以为1/2，3/2甚至5/2，键级越大，越容易稳定存在。

(1) 怎样理解化学中的成键轨道和反键轨道？
(2) 分子轨道理论简明读本---重点

前线轨道理论

DS

 

 

酸碱理论

酸碱质子理论(Bronsted理论)，在反应中给出质子的物质叫做酸在反应中接受质子的物质叫做碱。Bronsted酸就是常说的质子酸；Bronsted碱就是氢氧根离子。

酸碱电子理论(Lewis理论)，也称广义酸碱理论、路易斯酸碱理论。该理论认为：凡是可以接受外来电子对的分子、基团或离子为酸(路易斯酸)；凡可以提供电子对的分子、基团或离子为碱(路易斯碱，含有未共享电子对)。因为跳脱了限定氢离子与氢氧根的酸碱概念，这种理论包含的酸碱范围很广，但是，它对确定酸碱的相对强弱来说，没有统一的标度，对酸碱的反应方向难以判断。后来，拉尔夫·皮尔森提出的软硬酸碱理论弥补了这种理论的缺陷。

常见的Lewis酸：氯化铝、氯化铁、三氟化硼、五氯化铌以及镧系元素的三氟甲磺酸盐。(路易斯酸在有机化学的酸催化反应方面有重大的实践意义)
常见的路易斯碱：

常见的Lewis碱包括所有Bronsted碱，以及：
  1.负离子：卤离子、氢氧根离子、烷氧基离子、烯烃、芳香化合物
  2.带有孤电子对的化合物：氨、胺、醇、醚、硫醇、二氧化碳
  在有机化学中Lewis碱是亲核试剂。

亲核试剂是一种电子对供体，即路易斯碱。在反应过程中，它倾向于与电正性物种结合(与正电性碳反应)，因为原子核是电正性的，所以“亲核”即是指亲“电正性”。由于亲核试剂在反应中提供电子，按照Lewis酸碱理论，提供电子的为碱，因此，亲核试剂通常呈碱性。许多亲核反应在碱性条件下进行，了解亲核性与碱性的关系很重要。具有亲核性的原子可以是中性的，也可以带有负电荷。
(1) 孤对电子亲核试剂；(2) \(σ\)键亲核试剂；(3) \(π \)键亲核试剂。

亲电试剂：(1)路易斯酸亲电试剂；(2)\(π \)键亲电试剂；(3)\(σ\)键亲电试剂

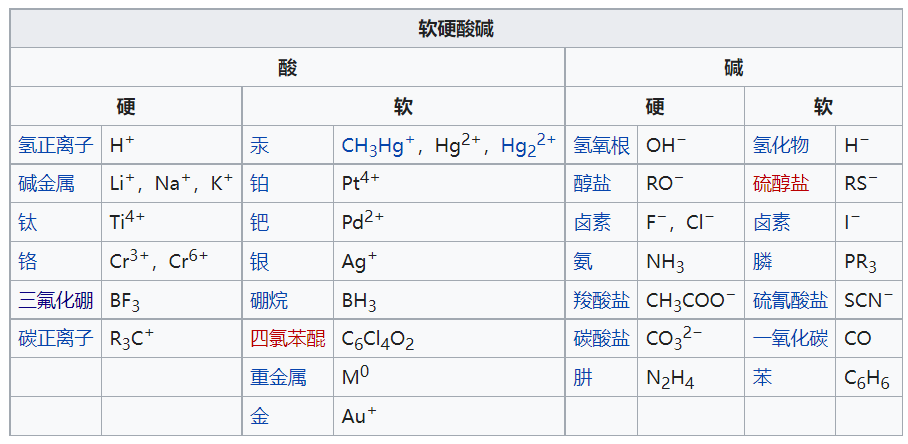
【软硬酸碱理论】简称HSAB(Hard-Soft-Acid-Base)理论，是一种尝试解释酸碱反应及其性质的现代理论。20世纪60年代初，拉尔夫·皮尔逊采用HSAB原理，尝试统一有机和无机化学反应。它目前在化学研究中得到了广泛的应用，其中最重要的莫过于对配合物稳定性的判别和其反应机理的解释。软硬酸碱理论的基础是酸碱电子论，即以电子对得失作为判定酸、碱的标准(即路易斯酸碱理论)。该理论可用于定性描述，而非定量的描述，这将有助于了解化学性质和反应的主要驱动因素。尤其是在过渡金属化学，化学家们已经完成了无数次实验，以确定配体和过渡金属离子本身的硬和软方面的相对顺序。

【硬】：是指那些具有较高电荷密度、较小半径的粒子(离子、原子、分子)，即电荷密度与粒子半径的比值较大。极化性(polarizable)较低，但极性较大。
【软】：是指那些具有较低电荷密度和较大半径的粒子。极化性较高，但极性较小。

主旨：在所有其他因素相同时，“软”的酸与“软”的碱反应较快速，形成较强键结；而“硬”的酸与“硬”的碱反应较快速，形成较强键结。大体上来说，“硬亲硬，软亲软”生成的化合物较稳定。

应用例子：In addition to the explicit reduction of Eu3+-based starting materials, several compounds containing polarizable anions with appreciable covalent bonding character, such as iodides, hydrides, heavy chalcogenides, and nitrides, readily stabilize Eu²⁺, sometimes even upon use of Eu³⁺-based starting materials. Among them, especially the class of Eu²⁺-activated nitridebased phosphors with their related narrow-band red emission has emerged to a promising class of inorganic materials that play a dominant role for phosphor-converted white-lightemitting diodes (pc-wLEDs).The stability of Eu²⁺ in the previously mentioned classes of compounds is chemically intuitively evident by means of Pearson's hard and soft acid and base (HSAB) principle. 参考Underestimated Color Centers: Defects as Useful Reducing Agents in Lanthanide-Activated Luminescent Materials

 

配位化合物

配位化合物(coordinationcompound)简称配合物，也叫错合物、络合物，为一类具有特征化学结构的化合物，由中心原子或离子(统称中心原子)和围绕它的称为配位体(简称配体)的分子或离子，完全或部分由配位键结合形成。

配位键(coordinate covalent bond，又称为配位共价键)，是一种特殊的共价键，当共价键中共用的电子对是有其中一原子独自供应时，就称为配位键。配位键形成后，与一般共价键无异。
配位键的形成条件：
(1) 一是中心原子或离子，它必须有能接受电子的空轨道；
(2) 二是有配位体，而且配位体中要键合的原子能提供孤对电子。

内界、外界：内界指配位单元，外界与内界相对。比如K₃[Cr(CN)₆]之中，内界是[Cr(CN)₆]^3–，外界是K⁺。内界离子很难电离，其电离程度很小。

 

 

化学动力学

Fundamental concepts in chemical kinetics-ChemTexts

化学平衡

Some Considerations on the Fundamentals of Chemical Kinetics: Steady State, Quasi-Equilibrium, and Transition State Theory

【勒夏特列原理】：又称为“平衡移动原理”，是一个定性预测化学平衡点的原理，其内容为—化学平衡是动态平衡，如果改变影响平衡的一个因素(温度/压力/浓度)，平衡就向能够减弱这种改变的方向移动，以抗衡该改变。这个原理只能用来定性判断，不能进行定量计算，不能首先判断平衡是否处于平衡态。

牛顿第三定律、楞次定律都和勒夏特列原理异曲同工。另外，在经济学方面，美国经济学家保罗·萨缪森于1947年提出了经济学的勒夏特列原理，这里勒夏特列原理把经济平衡的条件放得更宽：意指所有函数的未知数都是独立变数或辅助的约束条件—意指仅仅不改变最初的平衡状态—把反馈化约成参数改变。

【平衡常数】：可逆化学反应达到平衡时，每个产物浓度(或压强)系数次幂的连乘积与每个反应物浓度(或压强)系数次幂的连乘积成正比，这个比值叫做化学平衡常数，简称平衡常数，记作K。平衡时反应进行得越完全，平衡常数就越大。Reaction parameters like temperature, solvent, and ionic strength may all influence the value of the equilibrium constant. 平衡常数只和温度、溶剂种类、本性有关，而与反应速率、体系压强等无关。反应是否达到平衡，可以用K与反应商(Q，分为浓度商和压强商)来比较。

【基元反应】(Elementary reaction)：基元反应是指在反应中一步直接转化为产物的反应，又称为简单反应。从微观上看，反应物分子一般总是经过若干的简单反应步骤，才最后转化为产物分子的。每一个简单的反应步骤，就是一个基元反应。基元反应步骤要求反应物一步变成生成物，没有任何中间产物。按照基元反应定义，所有的可逆反应均为非基元反应。 拓展

【非均相反应】(Heterogeneous reaction)：又称“多相反应”，反应物是两相或两相以上的组分(固体和气体、固体和液体、两种互不混溶的液体)，或者一种或多种反应物在界面上(如固体催化剂表面上)进行的化学反应的总称。

【阿伦尼乌斯方程】：是化学反应的速率常数与温度之间的关系式，适用于基元反应和非基元反应，甚至某些非均相反应。其不定积分形式为：
\(k=A e^{-E_{a} / R T}\) 或 \( \ln k=-\displaystyle\frac{E_{a}}{R T}+\ln A \)
其中\( k\)为反应的速率常数，来自 \(\displaystyle\frac{d[C]}{d t}=k(T)[A]^{m}[B]^{n}\) (指数\( m\)和\( m\)称为反应级数，取决于反应机理，可由实验测定。将\( m\)和\( m\)相加，可得到反应的总级数)，\(A \)为频率因子(指前因子)。
此方程最早由荷兰化学家范托夫在1884年根据实验结果归纳得出。1889年，瑞典化学家阿伦尼乌斯进一步分析了范托夫提出的反应速率对温度的依赖关系，并从原理的角度对方程做了解释，提出反应中“能垒”(活化能)的存在。

注：阿伦尼乌斯方程阿伦尼乌斯方程一般适用于温度变化范围不大的情况，这时 \( A\)和 \(E_{a}\)变化不大，阿伦尼乌斯方程有很好的适用性。若温度范围较大，则阿伦尼乌斯方程会产生误差，这个时候可以用修正公式。阿伦尼乌斯方程是从经验推导而来，忽视了对机理的考虑。

 

过渡状态理论

【过渡状态理论】 (Transition state theory，TST)解释基元化学反应的反应速率。该理论假设在反应物和过渡态的【活化络合物】(activated complex)之间有一种特殊的化学平衡(准平衡，热力学平衡，满足玻尔兹曼分布)。该理论认为反应物分子并不只是通过简单碰撞直接形成产物，而是必须经过一个形成高能量活化络合物的过渡状态，并且达到这个过渡状态需要的一定的活化能，再转化成生成物。‡上标(the double-dagger symbol)表示过渡态。

过渡状态理论的基础思想如下：
(1) 通过研究建立在势能平面上的马鞍点处的活化络合物来研究反应速率。而该活化络合物是怎样形成的细节并不重要。
(2) 活化络合物与反应物分子处于特定的平衡(准平衡)。
(3) 活化络合物可以转化成不同的产物，而这种转化速率可以用动力学理论计算。

【Eyring方程】：补充

 

过渡态与中间体的区别：本质上二者都是反应过程势能曲线中导数为零的点，不同之处在于过渡态是势能处于极大值的那一点，而中间体是处于势能极小值的那一点。一般来说过渡态的存在时间为零，是能量极高点，有时候可以认为是旧键即将断裂(not quite broken)，新键即将生成(not quite formed)的瞬时状态。而中间体是有一定寿命的，具有一定程度上的稳定性，可以通过实验仪器观测到，最典型的比如SN1和SN2反应。下面两种情况来自organicchemistrytutor

 

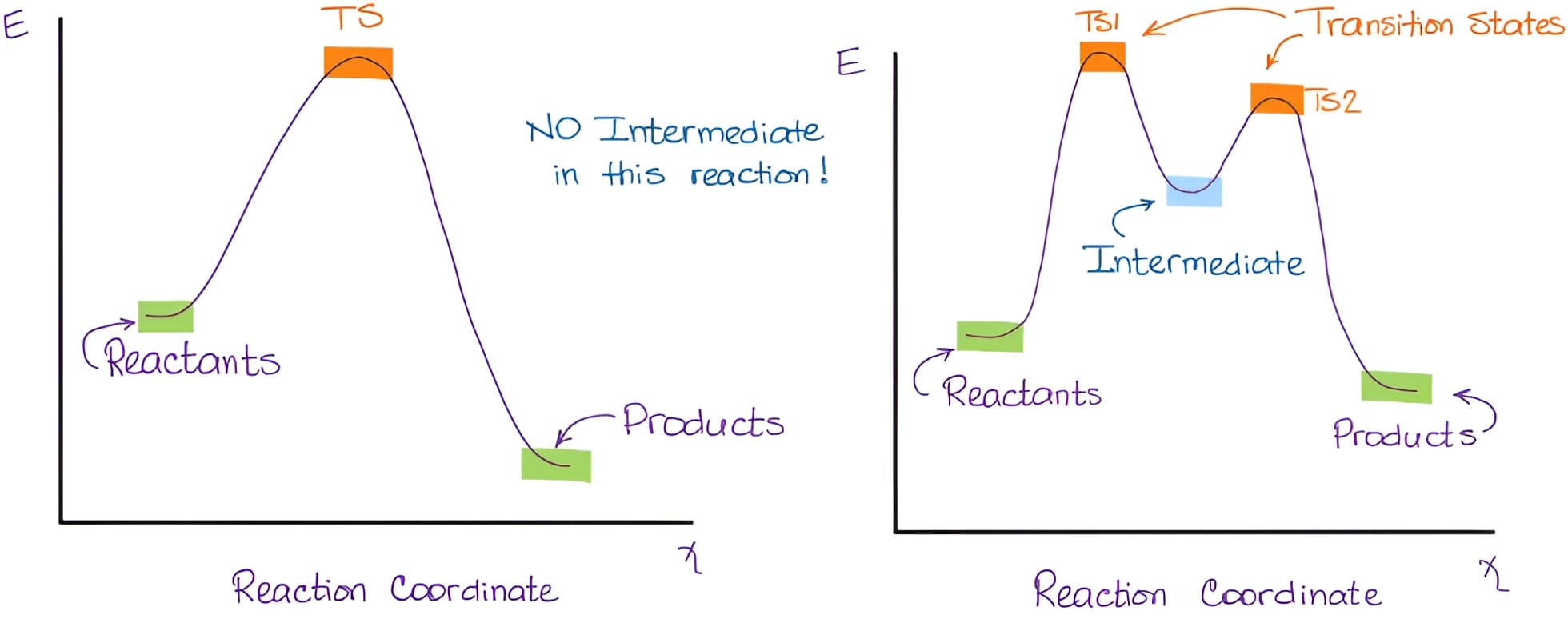
(1) 化学反应中过渡态与中间态有什么区别？
(2) 过渡态理论允许一个过渡态处在 monkey saddle point 上吗(此时的二阶导数为 0)？
(3) 过渡态理论与中间产物
(4)活化络合物(activated complex)和过渡状态(transition state)的区别
(5) 活化络合物

 

微分方程

参考:
(1) Some Considerations on the Fundamentals of Chemical Kinetics: Steady State, Quasi-Equilibrium, and Transition State Theory

 

Steady state和Equilibrium

【稳态】

• Steady state is established in kinetically controlled processes;
• A → B → C   (单位时间内由A生成的B的数量等于单位时间内由于生成C而消耗的B的数量，即B的浓度不随时间变化)
  In open systems, equilibrium can not be achieved but the steady-state can be achieved easily when incoming or outgoing heat or mass are equal
• There may be a transfer of heat due to an open system.
• The system is not at equilibrium which states that the entropy is increasing with time

【平衡态】

• Equilibrium is achieved in thermodynamically controlled processes.
• A ⇋ B  (单位时间内由A生成的B的数量等于单位时间内由于B生成A的数量，即A、B的浓度不随时间变化)
  In equilibrium, A can be changed into B and B can be changed into A, but net concentration remains constant
• In equilibrium, no net heat transfer due to a closed system.
• An equilibrium is established in a closed system.
  注：百度百科的介绍来看应该是孤立系统而不是封闭系统。平衡态(equilibrium state)是指在没有外界影响条件下热力学系统 的各部分宏观性质在长时间里不发生变化的状态。这里所说的没有外界影响，是指系统与外界没有相互作用，既无物质交换，又无能量传递(做功和传热)，即系统是孤立系。
• The entropy remains constant in equilibrium.
• In equilibrium, no net heat transfer due to a closed system.

参考资料：Difference between Steady State and Equilibrium—psiberg

 

化学热力学

几个热力学函数之间的关系：

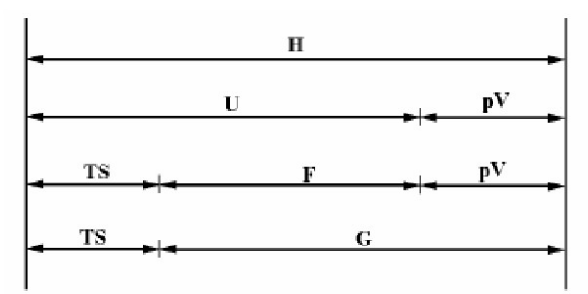
热动力势能(Thermodynamic potential)的概念：

(1) 内能：内能是指系统所含有的能量，但不包含因外部力场而产生的系统整体之动能与势能。内能是一系统内的状态函数，因为其值仅取决于该系统的目前状态，而与达到此一状态所采之途径或过程无关。虽然内能是个宏观物理量，内能也可在微观层面上由两个假设的量来解释。一个是系统内粒子的微观运动(平移、旋转、振动)所产生的微观动能。另一个是与粒子间的化学键及组成物质的静止质量能量等微观力有关之势能。就热力学及工程学上的实际用途来看，一般很少需要考虑一个系统的所有内含能量，如质量所含有的等价能量。一般而言，只有与研究的系统及程序有关的部分才会被包含进来。热力学一般只在意内能的“变化量”。

(2) 吉布斯自由能(也叫自由焓)：在等温等压状况(有的写恒温恒压，状态函数，强度量，不影响)下，一个热力过程具有自发性的必需条件为，吉布斯能随着过程的演化而减小。这意味着，平衡系统的吉布斯能是最小值；在平衡点，吉布斯能对于其它自变量的导数为零。

吉布斯自由能的变化可作为等温、等压过程(初态和末态压力)自发与平衡的判据，自由能变化为负，则反应可以自发进行。注意这种判断的前提是没有非体积功，或者说，反应过程中\( G\)的减少量是体系做非体积功的最大限度。这个最大限度在可逆途径得到实现。

\(G = H - TS\), 热力学自由能(包括吉布斯自由能和亥姆霍兹自由能)是指一个热力学系统的能量中可以用来对外做功的部分。简单的来说，自由能越大，这个系统的能量变成的另一种能量选择也就越多。所以说，其他条件相等的情况下，熵越大，自由能就越小，系统能量中能用来做功的部分越少，这个系统的“变数”越少。(参考知乎)

(3) 亥姆霍兹自由能：在物理学中也常直接简称为自由能，自由能可以被理解成是系统内能的一部分，这部分在可逆等温过程中被转化成功。\(F = U -TS\)或\( A = U -TS\)

(4) 焓：借用知乎1和知乎2答案可以形象理解，\(H = U+PV\)。把一个物体凭空变出来，除了需要增加该物体具有的内能\(U\)，还要排开该物体所占体积的空气，这个过程会做功\(PV\)，因此，焓可以理解为凭空变出一个物体需要的总能量。严格来说，焓并没有物理意义。

(5) 大势能：巨热力学势，也称作朗道自由能[1]，是统计力学中使用的一个量，特别是在开放系统的不可逆过程里使用。在统计力学中，它作为巨正则系综的特性函数出现。

初级概念
(1) 体积功和非体积功：热力学系统只因膨胀对外做功(或外界做功)称为体积功，而非体积功是诸如电/磁介质极化、表面张力等等做的功。(电功、表面功、光、轴功等)

(2) 自由膨胀：free expansion是一种不可逆的热力学过程，过程中气体在一个绝热的系统内膨胀(其实是向真空膨胀)，外界和系统之间没有功和热的交换。 真实气体在自由膨胀时会有温度的变化。若是理想气体，过程前后的温度不会变化，内能只和温度有关。

 

(3) 耗散过程：通过摩擦使功变为热的效应(摩阻、电阻、非弹性变性、磁阻等)。比如活塞中气体膨胀，如果活塞存在摩擦，那么系统对外界做的功大于外界得到的功。

(4) 准静态过程：在热力学里，准静态过程是系统总和环境处于热平衡的过程。现实中准静态过程不存在，但“足够(sufficiently)缓慢”的过程可视为一良好的近似。准静态过程可以可逆，亦可不可逆。当过程中熵增加时，则为不可逆。反之，任何可逆过程都必为准静态。但应注意若两物体间交换速率为一绝热的隔板所控制时，不论过程发生得如何缓慢，两个物体的状态都绝不会无限地趋近平衡态，因为热平衡需要两个物体具有绝对相同的温度(不太懂)。在有些文献中，对于准静态过程及可逆过程是有些模糊不明的，且有时它们会被当做同义词。准静态过程，既是平衡，又有变化。

弛豫时间：一个系统如果最初处于非平衡态，经过一段时间过渡到一个平衡态，这一过渡时间叫弛豫时间。

准静态过程的工程条件：破坏平衡所需时间(外部作用时间)远大于恢复平衡所需时间(弛豫时间)。

工程实例：活塞式内燃机 2000转/分，曲柄 2冲程/转，0.15米/冲程。活塞运动速度=2000*2 *0.15/60=10 m/s，而压力波恢复平衡速度(声速)350 m/s，远大于活塞运动的速度(压力波的速度对应于弛豫时间)。这里的弛豫时间是原来气缸内处于平衡态的气体受到压缩后再达到平衡态所需要的时间。首先要明白每一个静止的状态都是平衡的状态。那么当活塞移动时，就会打破平衡，缓慢移动就是说活塞移动使系统偏离平衡态的程度很小，有足够的时间(称为弛豫时间，这个时间相对于整个过程时间来说很小)来恢复平衡，进而可以认为系统总是处于平衡状态，也就是说活塞缓慢移动的过程是准静态过程。

一般的工程过程都可认为是准静态过程，具体工程问题具体分析。参考百度百科。

(5) 可逆过程：准静态过程 + 无耗散效应 = 可逆过程
在热力学中，可逆过程是指系统的某些属性能够在无能量损失或耗散的情形下通过无穷小的变化(准静态)实现反转的热力学过程(理想模型)。如果这一过程是一个热力学循环，则这种循环称为可逆循环。由于这些变化都是无穷小的，热力学系统在整个过程中都处于平衡态。由于在理论上这种过程所需时间为无穷大，完全理论意义上的可逆过程在实际中是不可能实现的。不过，如果系统对所发生变化的反应速度远远大于变化本身，过程中微小的不可逆性则可以忽略，因而理论上经常把无摩擦的准静态过程看作可逆过程。在可逆循环中，系统和其外界环境在每一次循环结束时都保持完全相同的状态。

可逆过程的另一种定义是，过程发生后能够被复原并对系统本身或外界不产生任何影响的过程称作可逆过程。在热力学的语义中，一个过程“发生”是指这个热力学系统从初始状态发生变化直到终止状态过程结束。

可逆过程总是准静态的，但反过来并不总是正确的。例如，在活塞和气缸之间存在摩擦的气缸中对气体进行无限小压缩是准静态的，但不是可逆过程。尽管系统仅以极小的量从其平衡状态被驱使，但由于摩擦，热量已不可逆转地损失，并且无法通过简单地向相反方向无限地移动活塞来恢复。

自然界中一切与热现象有关的实际过程，具有共同的特征，这就是它们的不可逆性，并且所有不可逆过程都存在内在联系，而反映这种共同特征和这种内在联系的，就是热力学第二定律。

绝热的可逆过程才是等熵过程。可逆过程的充要条件是准静态过程 + 无耗散效应，并不一定绝热。

引入可逆过程的意义：

• 准静态过程是实际过程的理想化过程， 但并非最优过程，可逆过程是最优过程。
• 可逆过程的功与热完全可用系统内工质的状态参数表达，可不考虑系统与外界的复杂关系，易分析。
• 实际过程不是可逆过程，但为了研究方便，先按理想情况(可逆过程)处理， 用系统参数加以分析，然后考虑不可逆 因素加以修正。

几种典型的可逆反应：

• 可逆膨胀和可逆压缩：力学平衡。(从同一状态出发经过不同绝热过程到达相同的体积(或相同的压力)，则其中可逆过程的功最大)
• 可逆传热：热平衡
• 可逆相变：相平衡
• 可逆化学反应：A ＋ B ⇔ C

(6) 不可逆过程：实际过程进行有方向性，满足能量守恒，但是不能返回原状态。常见的不可逆过程有不等温传热、节流过程、自由膨胀、混合过程。具体来说，在不考虑耗散下，高压气体通过活塞向外等温膨胀，从状态A到状态B膨胀对外做的功为W₁，然后外界压缩气体使之回到A状态，外界对系统做的功为W₂，显然W₂大于W₁，即在环境中留下了影响。

(7) 等熵过程：
准静态过程＞可逆过程＞等熵过程
其中，无耗散效应的准静态过程，方为可逆过程。绝热可逆过程，方为等熵过程，意即可逆过程未必是等熵过程。

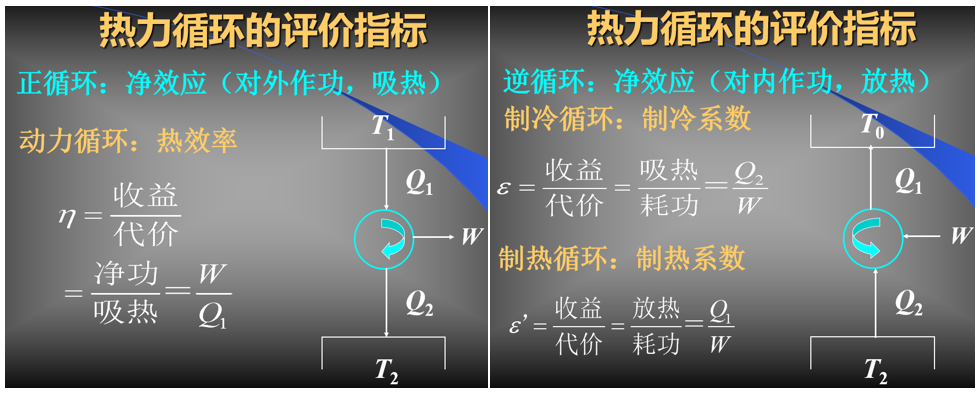
(8) 热力循环的评价指标：参考李永乐老师9分钟讲解热机原理和卡诺定理

(9) 热容
不考虑相变和非膨胀功的情况下(其实就是理想气体)，等压和等容热容：$$\begin{aligned} &C_{p}(T)=\frac{\delta Q_{p}}{\mathrm{~d} T}=\left(\frac{\partial H}{\partial T}\right)_{p} \quad\Delta H=Q_{p}=\int C_{p} \mathrm{~d} T \\ &C_{V}(T)=\frac{\delta Q_{V}}{\mathrm{~d} T}=\left(\frac{\partial U}{\partial T}\right)_{V} \quad\Delta U=Q_{V}=\int C_{V} \mathrm{~d} T \end{aligned}$$对于理想气体，根据微分性质以及麦克斯韦关系式，可以得到$$C_{p}-C_{V}=n R \quad \text { 或 } \quad C_{p, \mathrm{~m}}-C_{\mathrm{V}, \mathrm{m}}=R$$

(10) 节流过程与焦耳-汤姆孙(Joule-Thomson)实验
焦耳-汤姆孙效应(理想气体无该效应)是指气体会因在等焓的环境下膨胀，而使温度上升或下降。这个过程称为焦耳-汤姆孙过程。焦耳汤姆孙系数：\( \mu_{J T}=\left(\frac{\partial T}{\partial P}\right)_{H}\)。详情见课件和维基。

(11) 自发过程
在一定环境条件下，(环境)不作非体积功，系统中自动发生的过程。反之，只有(环境)作非体积功方能发生的过程为非自发过程。通常所说的“过程方向”即是指自发过程的方向。比如气流从高压区到低压区，热量从高温区传到低温区，物质从高浓度的地方扩散到低浓度的地方，HCl和NaOH反应生成NaCl和H₂O，功转化为热。自发过程的共同特征：
(a) 自发过程单向地朝着平衡。
(b) 自发过程都有作功本领。
(c) 自发过程都是不可逆的。

自发过程的内容来自朱文涛的ppt，维基百科上关于自发过程的描述如下：自发过程，是系统随时间释放自由能、移往自由能更低且更加热力学平衡的能量状态的过程。自由能变化的正负值取决于热力学的测量传统。当系统释放自由能能，系统自由能变化为负值。随着过程的条件不同，所采用的自由能也不相同。例如，当考虑恒温恒压过程中，应采用吉布斯自由能，而考虑恒温恒容过程时，应采用亥姆霍兹自由能。由于降低系统自由能为自发过程的特色，因此该过程不需要外接提供能量即可发生。在孤立系统的情形下，系统边界无任何能量交换，增加系统熵的方向为自发过程的方向。

一般而言，过程的自发性只决定该过程是否“能够”自发，但并不代表该过程“将会”发生。换句话说，自发性是必须的，但并不足以使过程发生。此外，自发性也无法决定该过程之速率快慢。比如说，于室温常压下，钻石转化成石墨是一个自发的过程。尽管如此，这个自发过程却是极缓慢的。

(12) 熵：很多情况下，近似认为反应的熵变基本不随温度而变。

热力学四定律

热力学第零定律：若两个热力学系统均与第三个系统处于热平衡状态，此两个系统也必互相处于热平衡。
(a) 数学上，第零定律表示这是一种等价关系。
(b) 第零定律说明任何两个系统的热平衡关系都是等价的，而经常被认为可于建立一个温度函数；更随便的说法是可以制造温度计。

热力学第一定律：(多种阐述，适用于非敞开系统，没有物质交换)

(a) 物体内能的增加等于物体吸收的热量和对物体所作的功的总和。
(b) 系统在绝热状态时，功只取决于系统初始状态和结束状态的能量，和过程无关。
(c) 孤立系统的能量永远守恒。
(d) 系统经过绝热循环，其所做的功为零，因此第一类永动机是不可能的(即不消耗能量做功的机械)。
(e) 两个系统相互作用时，功具有唯一的数值，可以为正、负或零。

热力学第一定律从历史上看，是一个“定律”，也就是说是总结出来的。但现代物理学已经把能量守恒定律作为“定律”来看待，那么热力学第一定律实际上是能量守恒定律的一个“推论”。热力学第一定律的最大价值是引入了一个具有能量量纲的状态量——内能。其含义有两个：
(a) 一个是做功与传热在改变热力学平衡态的效果上具有等价性；
(b) 二是改变热力学平衡态的方法只有做功与传热两种途径。

第一类永动机试图以机械的方式在不获取能源的前提下使体系持续地向外界输出能量。

参考资料：李永乐老师讲热力学第一定律

热力学第二定律：(多种阐述)
(a) 克劳修斯表述：不可能把热量从低温物体传递到高温物体而不产生其他影响。

克劳修斯表述是以热量传递的不可逆性(即热量总是自发地从高温热源流向低温热源)作为出发点。虽然可以借助制冷机使热量从低温热源流向高温热源，但这过程是借助外界对制冷机做功实现的，即这过程除了有热量的传递，还有功转化为热的其他影响。

(b) 开尔文表述：不可能从单一热源吸收能量，使之完全变为有用功而不产生其他影响。

开尔文表述是以第二类永动机不可能实现这一规律作为出发点。第二类永动机是指可以将从单一热源吸热全部转化为功，但大量事实证明这个过程是不可能实现的。功能够自发地、无条件地全部转化为热；但热转化为功是有条件的，而且转化效率有所限制。也就是说功自发转化为热这一过程只能单向进行而不可逆。开尔文表述也说明了热机的效率不可能达到100 %。

1.开尔文表述和克劳修斯表述是等价的。

2. 网友也说了一种理解方式“其实这还是力学,当两个速度不一的分子互相撞击时,速度快的会变慢,速度慢的会变快”。

3. 热力学第二定律代表了自然界的前进方向，有些事情是可以发生的，有些事情虽然满足能量守恒，但是不能发生。能量是在转化和守恒过程中的，但是能量的品质是有区别的，高温热源向低温热源传递热量，二者温度相等，就不能再做功了，我们就称之为能量的品质降低了。

4. 热机的做法都是有两个热源，低温热源，高温热源，从高温热源吸收一部分热，这部分热一部分给了低温热源，剩下的部分才是用来对外做功。内燃机就是一个例子，如果周围的空气和内燃机的温度是一样的，那么就无法对外做功，对外做功的前提是有温度差。

5.热功转换的不等价性，功可以无代价地全部变为热，但热全部变功必须付出代价(系统和环境)，若不付代价只能部分变功。

6. 参考资料：李永乐-热力学第二定律是什么？“麦克斯韦妖”是什么鬼？

麦克斯韦妖：事实上，区分速度快的分子是需要能量的。

热力学第三定律：

为“在热力学温度零度(即T=0 K开)时，一切完美晶体的熵值等于零。”所谓“完美晶体”是指没有任何缺陷的规则晶体。绝对零度不可达到。从能斯特热定律的角度来描述：当系统趋近于绝对零度时，一化学或物理变化之熵变化量趋近于零。这样的叙述可以数学式表示之：$$\lim _{T \rightarrow 0} \Delta S=0$$

等温等压下\( \Delta G=\Delta H-T \Delta S\)，而对大多数化学反应来说，温度对反应自由能的影响要远大于反应物的分压(及浓度)的影响。However, it is known from thermodynamics that the slope of the ΔG curve is -ΔS. Since the slope shown here reaches the horizontal limit of 0 as T → 0 then the implication is that ΔS → 0, which is the Nernst heat theorem.

能斯特热定律/热力学第三定律为任意状态下物质的熵值提供了相对标准，其实第三定律只是一种规定，因为人们将以此规定为基础计算出其他状态下的熵称为规定熵(标准摩尔熵(标准摩尔熵指在标准状况(298.15 K，10⁵ Pa)下，1摩尔纯物质的规定熵)。也就是说，热力学第三定律选了一种假想的状态作为熵的零点。

麦克斯韦关系式：
该关系式是热力学中的一套方程，可以从热力学势的定义推出，麦克斯韦关系式是热力学势的二阶导数之间的等式的陈述。它们可以直接从二元解析函数的高阶导数与求导次序无关的事实推出。如果\(\Phi\)是一个热力学势，\(x_i\)和\(x_j\)是这个势的两个不同的自然变量，那么这个势和这些变量的麦克斯韦关系式为：$$\frac{\partial}{\partial x_{j}}\left(\frac{\partial \Phi}{\partial x_{i}}\right)=\frac{\partial}{\partial x_{i}}\left(\frac{\partial \Phi}{\partial x_{j}}\right)$$

四个最常见的麦克斯韦关系式是四个热力学势的二阶导数的等式，关于它们的热自然变量(温度\( T\) 或熵\( S\) )和机械自然变量(压强\( P\) 或体积\( V\) )：

吉布斯和亥姆霍兹自由能之间的区别

化学热力学的应用实例

热力学方程在计算热力学函数中的应用

盖斯定律(Hess's law)：又名反应热加成性定律，若一反应为二个反应式的代数和时，其反应热为此二反应热的代数和。也可表达为在条件不变的情况下，化学反应的热效应只与起始和终了状态有关，与变化途径无关。

1.通过热力学参量来计算结合能或晶格能。例如，MgO的晶格能可以通过如下的循环来求得
等式右边各参量都可测量，则晶格能可由实验数据计算出来。

2.计算热缺陷浓度

对于单质晶体，假设晶体由 \( N\)个原子构成，在温度\( T\)时，形成\( n\)个孤立空位空位较少， 彼此相距较远时，可以认为相互孤立(空位较少， 彼此相距较远时，可以认为相互孤立)。
\( \Delta G_{\mathrm{S}}\)为 形成一个肖特基缺陷时系统自由焓的变化。 一般情况下 \( N \gg n\)，则有$$\frac{n}{N}=\exp \left(-\frac{\Delta G_{s}}{k T}\right)$$如果是 MX型晶体，由于正负离子空位成对出现，用类似方法可得肖特基缺陷浓度为$$\frac{n}{N}=\exp \left(-\frac{\Delta G_{s}}{2 k T}\right)$$推导的公式参考《材料科学基础》，依据是 当系统自由焓最低时，即\( \frac{\partial \Delta G}{\partial n}=0\)系统达到平衡。

弗伦克尔缺陷浓度的表达式为$$\frac{n}{N}=\exp \left(-\frac{\Delta G_{F}}{2 k T}\right)$$ \( \Delta G_{\mathrm{F}}\)为形成一个弗伦克尔缺陷的自由焓变化。

还可以根据质量作用定律，可以利用化学平衡方法计算热缺陷的浓度 。 以CaF2晶体为例，形成肖特基缺陷时，反应方程式为:\(\mathrm{O}(\text { naught }) \longrightarrow \mathrm{V}_{\mathrm{Ca}}^{\prime \prime}+2 \mathrm{~V}_{\mathrm{F}}^{\bullet} \)平衡常数\(K=\frac{\left[\mathrm{V}_{\mathrm{Ca}}^{\prime \prime}\right]\left[\mathrm{V}_{\mathrm{F}}^{\bullet}\right]^{2}}{[\mathrm{O}]}=\frac{4\left[\mathrm{~V}_{\mathrm{Ca}}^{\prime \prime}\right]^{3}}{[\mathrm{O}]}\)其中\( [\mathrm{O}]=1\)，即 无缺陷状态的浓度。 物理化学知识可知，上述缺陷反应的摩尔自由焓变化\(\Delta G=-R T \ln K\)，于是\(  \left[V_{\mathrm{Ca}}^{\prime \prime}\right]=\frac{1}{\sqrt[3]{4}} \exp \left(-\frac{\Delta G}{3 R T}\right)\)，其中\(  \Delta G\) 为形成1 mol肖特基缺陷的自由焓变化。 

3.介稳性

在一定的热力学条件下，系统虽未处于最低能量状态，却处于一种可以较长时间存在的状 态，称为处于介稳状态。当熔体冷却成玻璃体时，其状态不是处于最低的能量状态。它能较长时间在低温下保留高温时的结构而不变化。因而为介稳状态或具有介稳的性质，含有过剩内能。从热力学观点看，玻璃态是一种高能量状态，它必然有向低能量状态转化的趋势，也即有析晶的可 能。然而事实上，很多玻璃在常温下经数百年之久仍未结晶，这是由于在常温下，玻璃粘度非常大，使得玻璃态自发转变为晶态很困难，其速率是十分小的。因而从动力学观点看，它又是稳定的。

4.润湿

从微观角度看，润湿固体的流体，在置换原来在固体表面上的流体后，本身与固体表面是在分子水平上的接触，它们之间无被置换相的分子。

润湿现象可以分为沾湿、浸湿和铺展三种类型。

(1) 沾湿：若设固-液接触面为单位面积，在恒温恒压下，此过程引起体系自由能的变化为\(\Delta G=\gamma_{S L}-\gamma_{S V}-\gamma_{L V}\)，等式右边分别为单位面积固-液、固-气和液-气的截面自由能。固-液界面张力总是小于它们各自的表面张力之和，这说明固-液接触时，系统自由能变化小于零，沾湿过程可以自发进行。

(2) 浸湿：若固体小方块的总面积为单位面积，则在恒温恒压下，浸润过程引起的自由能的变化为：\(\Delta G=\gamma_{S L}-\gamma_{S V}\)。浸湿过程与沾湿过程不同，不是所有液体和固体均可以自发发生浸湿，只有固体的表面自由能比固-液的界面自由能大时浸湿过程才能自发进行。

(3) 铺展：在恒温恒压下，若液滴在固体表面上自动展开形成液膜，设液体在固体表面上展开了单位面积，则体系自由能的变化为\(\Delta G=\gamma_{S L}+\gamma_{L V}-\gamma_{S V}\)。

上面讨论的三种情况的条件都是在无外力作用下液体自动润湿固体表面的条件。固体表面自由能和固-液界面自由能，无法测定，但是我们可以定性分析三种情况。如果想要水滴在石蜡表面展开，一般的做法是在水里加表面活性剂，因为表面活性剂在水表面和水-石蜡界面上吸附可以使得\(\gamma_{L V}\)和\(\gamma_{S L}\)降低，而\(  \gamma_{S V}\)不易增加。

接触角和Young方程：目前不能定量地判断一种液体能否润湿某一种固体，但是可以通过接触角来解决问题。

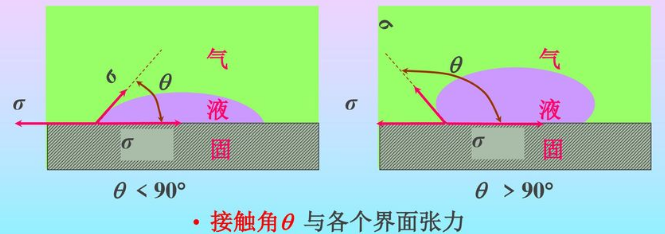
$$\cos \theta=\frac{\gamma_{S V}-\gamma_{S L}}{\gamma_{L V}}$$\( \theta \leqslant 180^{\circ}\)沾湿(永远成立，自发过程)，\(\theta \leqslant 90^{\circ}\)浸湿，\(\theta=0^{\circ}\)铺展。固体表面粗糙下接触角更小。

应当指出，Young方程的应用条件是理想表面，即指固体表面是组成均匀、平滑、不变形(在液体表面张力的垂直分量的作用下)和各向同性的。只有在这样的表面上，液体才有固定的平衡接触角，Young方程才可应用。

参考资料：物理化学PPT

讨论：上述模型其实是针对(理想)光滑表面而言的，然而现实中的固体表面往往
并不是理想光滑的，对于粗糙表面上的水滴，润湿状态可以被 Wenzel 模 型和 Cassie-Baxter 模型来描述
参考：《基于特殊润湿性材料的油水分离》

莲花效应 (lotus effect)，也称作荷叶效应，是指莲叶表面具有超疏水性以及自洁(self-cleaning)的特性。在东方文化里，莲花是纯净的象征。虽然，莲花喜欢生长在泥泞的湿地，但其叶子和花仍保持干净，这就是自洁的效果。植物学家研究莲叶表面发现它们有一个自然洁净的机制。
花瓣效应 ： (有待拓展)

5.相变的热力学分类

spinodal decomposition

6.相变过程的温度条件

由热力学可知，在等温、等压下有：$$\Delta G=\Delta H-T \Delta S$$在平衡条件下\(\Delta G=0\)，则有\(\Delta H-T \Delta S=0 \)，于是\(\Delta S=\Delta H / T_{0}\)，其中\( T_{0}\)为相变的平衡温度，\(\Delta H\)为相变热。若在任意一温度的不平衡条件下，则有吉布斯自由能变不为零。如果\(\Delta H\)和\(\Delta S\)不随温度而变化，那么$$\Delta G=\Delta H-\frac{T \Delta H}{T_{0}}=\Delta H \frac{T_{0}-T}{T_{0}}=\Delta H \frac{\Delta T}{T_{0}}$$若相变过程放热(比如凝聚、结晶等)，\(\Delta H<0\)，要使\(\Delta G<0\)，必须有\(\Delta T>0\)，即系统必须"过冷"，也就是系统实际温度比理论相变温度要低，才能使相变过程自发进行。同理，如果相变过程吸热(如蒸发、熔融等)，系统自发相变则必须“过热”。由此可知：相变驱动力可以表示为过冷度(过热度)的函数，因此相平衡理论温度与系统实际温度之差即为相变过程的推动力。

7.相变过程的温度条件

从热力学知道，在恒温可逆非体积功为零时：$$\mathrm{d} G=V \mathrm{~d} p$$ 对理想气体而言$$\Delta G=\int V \mathrm{~d} p=\int \frac{R T}{p} \mathrm{~d} p=R T \ln \frac{p_{2}}{p_{1}}$$ 当过饱和蒸汽压力为\(p\)的气相凝聚成液相或固相(其平衡蒸汽压力为\(p_0\))时，有\(\Delta G=R T \ln \frac{p_{0}}{p}\)。 要使相变能自发进行，必须\(\Delta G<0\)，即\(p>p_{0}\) ，也即要使凝聚相变自发进行，系统的饱和蒸汽压应大于平衡蒸汽压 。这种过饱和蒸汽压差为凝聚相变过程的推动力。

对溶液而言，可以用浓度\( C\)代替压力\(p\)，于是\(\Delta G=R T \ln \frac{C_{0}}{C}\)。 若是电解质溶液还要考虑电离度\( \alpha \)，即一个摩尔电解质能离解出\(  \alpha \)mol 离子，则$$\Delta G=\alpha R T \ln \frac{C_{0}}{C}=\alpha R T \ln \left(1+\frac{\Delta C}{C}\right) \approx \alpha R T \cdot \frac{\Delta C}{C}$$ 要使相变过程自发进行，应使\(C>C_{0}\)， 液相要有过饱和浓度，它们之间的差值即为 这一相变过程的推动力。

综合6和7有：相变要自发进行，系统必须过冷(过热)或过饱和，此时系统温度、浓度和压力与相平衡时温度、浓度和压力之差值即为相变过程的推动力。

 

 

趣味化学

• a List of smelly inorganic substances