图床：chemistry-img/

1.气体

1. 什么是等离子态（plasma state）?[mathjax] 答：等离子态不同于固、液、气态，等离子态是由大量带正负电荷的粒子、电子以及少量未被电离的分子、原子等，是一种新的导电流体，但是整体还是呈现电中性。如闪电、极光等。

2. 理想气体状态方程和Dalton气体分压定律？
答：\(p V=n R T\)
混合气体的总压力等于各个气体分压的总和

3. 摩尔气体常数R的测量？
答：我们知道实际气体在压力很小的时候是很接近理想气体的，那么应该可以直接利用\(p V=n R T\)测量实际气体的摩尔气体常数，但是这个时候实验的测量误差比较大，这个时候我们可以采用外推的方式测量，测不同压力下的R值，然后外推到压力为0的时候的R值。外推法（extrapolation [ɪkˌstræpəˈleɪʃn] ）是实验中的常用方法。

4. 理想气体状态图等温线（isotherm）；等压线（isobar）

5. Maxwell速率分布定律是什么？
答：$$f(v)=\frac{4}{\sqrt{\pi}}\left(\frac{m}{2 k T}\right)^{1.5} \exp \left(\frac{-m v^{2}}{2 k T}\right) v^{2}$$这里表示的是一个连续随机变量的“概率密度函数”，也就是单独研究一个给定速率的气体分子的含量是没有意义的，因为速率是一个连续变量，可以无线分割，只有研究某一范围的速率分子的比例（或者数量）才是有意义的，可以用对应区域的面积来表示。
6. 分子运动速率的几个重要统计平均值？
答：分别是最概然速率，平均速率，以及均方根速率。可以由上面的图理解对应的含义。

7. 什么是分子射线束实验？
答：分子射线束实验，是用来验证前面的分子运动速率分布的。
金属气体蒸汽，从A中小孔射出，然后经过定向狭缝S，改变S1和S2的转速，就可以测量不同速率的蒸汽。
        概率论中指出，测定某一速率范围的分子数的统计平均值为\(\Delta n\)，那么实际分子数对于这个统计平均值的偏移范围即涨落幅度基本上是\(\pm \sqrt{\Delta n}\)，所以分子数越多，统计的相对误差就越小，得到的速率分布就更接理论值。

8. 分子平均动能分布式怎样的？
动能分布函数为$$f(E)=\frac{2}{\sqrt{\pi}}\left(\frac{1}{k T}\right)^{1.5} \mathrm{e}^{-\frac{E}{k T}} E^{\frac{1}{2}}$$如下图所示
通常在物理化学中，都假定分子在二维平面运动，这样简化之后，可以得到
$$\frac{N_{E_{1} \rightarrow \infty}}{N}=e^{-\frac{E_{1}}{k T}}$$也就是能量超过E1的分子的比例，继续延伸，可以得如下关系式：$$ \frac{N_{E_{2} \rightarrow \infty}}{N_{E_{1} \rightarrow \infty}}=e^{-\frac{\left(E_{2}-E_{l}\right)}{k T}}=e^{-\frac{\Delta E}{R T}}$$这和玻尔兹曼分布很像（在两个能量状态都的简并度g相等的情况）

9. 重力场对气体分子分布的影响？
答：无规则的热运动使得气体分子均匀分布在整个空间，但是重力的作用又使得气体分子倾向于下沉，综合起来的作用就是上面气体稀薄，下面气体浓度高。在研究大气层问题的时候，就必须考虑重力场的影响。

10. 什么是气体分子碰撞的平均自由程？
答：分子每两次碰撞间走过的路程叫作自由程（free path）。大量自由程的平均值就是平均自由程。两个分子碰撞时，质心能达到的最小距离称为有效直径或者说碰撞直径，往往要大于分子本身的直径（靠得很近的时候，斥力很大）。
不同分子的碰撞与化学反应的速率直接有关。

11. 实际气体与理想气体状态方程的关系？
答：

实验发现，在低温、高压时，真实气体的行为与理想气体定律的偏差很大。这是由于在低温、高压下，气体的密度增大，分子间的距离缩小，分子间的相互作用以及分子自身的体积就不能略去不计，不能把分子再看作是自由运动的弹性质点，因此理想气体的分子运动模型需要予以修正。

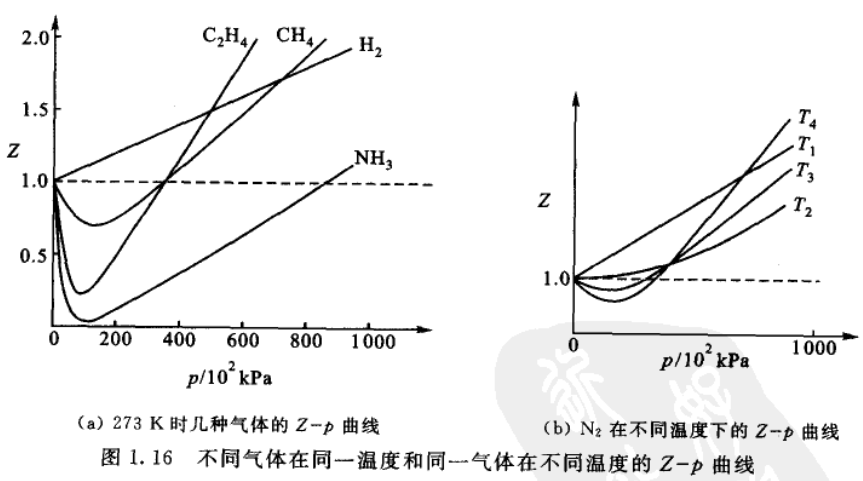图(b)中\(T_4\)的温度最低，\(T_1\)的温度最高。温度为\(T_2\)时，此时曲线以较缓的趋势趋向于水平线，并与水平线\(Z=1\)相切。此时在相当一段压力范围内\(Z \approx 1\)，随压力变化不大，并符合理想气体状态方程。此时的温度称为波义尔温度，图形上表现为在此温度时，等温线的坡度等于零，即$$$$

范德华方程 $$\left(p+\frac{a}{V_{\mathrm{m}}^{2}}\right)\left(V_{\mathrm{m}}-b\right)=R T$$里面有两个具有物理意义的修正因子\(a\)和\(b\)，这两个因子揭示了实际气体和理想气体差异的根本原因。
（1）压力较大的时候，实际气体分子的体积无法忽略，所以引入纠正系数b，也就是实际体积是原来的体积减去气体分子所占的体积\(b\)（见图1.13(b)）。
（2）对于靠近容器壁的分子来说，后面的分子对它施加吸引力，趋向于把分子向后拉，所以气体施于器壁的压力要比忽略引力时（看作理想气体）小。这一部分的大小和容器内的气体分子数目成正比，又和碰撞的分子数目成正比，两个数目都是N，其实最终就是和密度的平方成反比。上式是气体为1mol时候的方程。实际是如下：
$$\left(p+\frac{a n^{2}}{V^{2}}\right)(V-n b)=n R T$$

12. 气体和液体之间的转变？
13. 压缩因子图？

2.热力学

1. 基本内容简介？
待续

2. 冬天，在户外，手去触摸铁器和触摸木材，感受到的温度不一样，为什么？
答：手感受到的温度不一样，并不是说铁器温度更低，木材温度更高，二者的温度是一样高，人感受到的差别是因为传热速率的不同导致的。铁传热快，所以手的热可以迅速传递给铁，人就感觉冰冷。

3.  什么是热力学第零定律？
答：如果两个系统分别和处于确定状态的第三个系统达到热平衡，则这两个系统彼此也将处于热平衡。这个热平衡的规律成为“热力学第零定律”，这个定律是对实验的总结和概括，并不能由其他的定律推导出来（类似F=ma）。这个定律时间上是在第一和第二之后提出的，但是逻辑上，这个定律是更根本的，是基石，所以排在前面，称为第零定律。
第零定律→“温度”的概念，指出了温度这个状态函数的存在，而且可以用导热实验来判断不同物体的温度大小。

4. 热力学的一些基本概念？
答： 三种系统：隔离系统、封闭系统、敞开系统
广度量：具有加和性；比如体积、质量、熵、热力学能等。一次齐函数
强度量：不具有加和性；比如温度、压力、密度、粘度等。零次齐函数
四种平衡：热动平衡（thermal）、力学平衡（mechanical）、相平衡（phase）、化学平衡（chemical）
状态函数（state function）: 异途同归，值变相等；周而复始，数值还原。数学上具有全微分的性质。
状态方程：
过程和途径（process and path）：等温、等容、等压、绝热、环状过程；系统由是始态到终态的变化可以经过不同的步骤，这种具体的步骤成为途径（path）。状态函数与途径无关。

热和功：热就不多说了；功的形式有机械功、电功、反抗地心引力的功、膨胀功、表面功。强度因素的大小决定了能量的传递方向，而广度因素则决定了功值的大小。强度因素可以看做一种“广义的力”。
5. 什么是卡路里？
答：卡路里（calorie），简写cal，是一个能量单位，简单地说，1卡路里的能量可以将1克水在一个大气压下的温度升高1摄氏度。食品上列出的是“大卡”，也就是1000卡路里。

6. 什么是热力学第一定律？
答：多种描述方式：
1. 物体内能的增加等于物体吸收的热量和对物体所作的功的总和。
2. 系统在绝热状态时，功只取决于系统初始状态和结束状态的能量，和过程无关。
3. 孤立系统的能量永远守恒。
4. 系统经过绝热循环，其所做的功为零，因此第一类永动机是不可能的（即不消耗能量做功的机械）。
热力学第一定律也是人类经验的总结。
$$\Delta U=U_{z}-U_{1}=Q+W\\
\mathrm{d} U=\delta Q+\delta W$$

系统的总能量\(E\)是由三部分组成：(1)系统整体运动的动能\(T\);(2)系统在外力场中的位能\(V\);(3)热力学能\(U\)(thermodynamic energy)，也称为内能（internal energy）。化学热力学通常研究的是宏观静止的系统，而且没有外力场，只考虑第三项。热力学能是指系统内分子运动的平动能、转动能、振动能、电子及核的能量，以及分子与分子相互作用的位能等能量的总和。

7. 准静态过程？
假定上述是一个恒温过程$$\delta W=-F_{e} \mathrm{d} l=-\left(\frac{F_{\mathrm{e}}}{A}\right)(A \mathrm{d} l)=-p_{\mathrm{e}} \mathrm{d} V$$(1) 自由膨胀（free expansion），不对外做功
(2) 外压始终维持恒定
(3) 多次（无限次）等外压膨胀
上面是系统对外膨胀，下面是外界对系统做功（压缩）；右侧两个都是准静态过程，也就是说外界和系统的压力差是无限小，整个过程需要的时间是无限大。准静态过程是一个理想过程，实际上是办不到的。对于准静态过程，在膨胀过程中系统做功最大，在压缩过程环境对系统做功最小，总而言之就是使得系统能量尽可能小。
可逆过程的功$$W_{ }=-\int _{ V_{ 1 } }^{ V_{ 2 } } p_{ { i } }{ d }V=-\int _{ V_{ 1 } }^{ V_{ 2 } } \frac { nRT }{ V } { d }V=-nRT\ln { \frac { V_{ 2 } }{ V_{ 1 } } } $$

8. 什么是可逆过程？
答：可使得系统和环境都回到原来状态的过程。上述的准静态膨胀/压缩过程在没有任何耗散，例如没有因为摩擦而造成的能量的散失等的情况下就是一种可逆过程。举个例子，如果在等温过程中，将系统对环境做的功储藏起来，这些功恰能使得系统回到原来的状态，同时将膨胀时所吸收的热还给热储器。
                                    准静态过程 + 无耗散效应 = 可逆过程
接近于可逆的实际情况：液体在沸点附时的蒸发，固体在熔点时的熔化，可逆电池在外加电动势与电池电动势近似相等情况下的充电和放点。

9. 什么是焓(enthalpy)？
答：如果只涉及体积功，那么有：\(\Delta U=Q+W\)，对于等容过程：
\(\Delta U=Q_V\)。
对于等压过程：\(U_{2}-U_{1}=Q_{p}-p\left(V_{2}-V_{1}\right)\)，
\(Q_{p}=\left(U_{2}+p V_{2}\right)-\left(U_{1}+p V_{1}\right)\)。于是定义焓：\(H \stackrel{\text { def }}{=} U+p V\)
        焓并没有确切的物理意义，之所以要定义这个新的函数，纯粹是因为很实用，处理热力学化学的计算更方便。
        对于等容过程，吸收的热量全部转化为内能；对于等压过程，吸收的热量全部转化为焓。

10. 什么是热容？
答：不考虑相变和非膨胀功的情况下，等压和等容热容

11. 内能和温度的关系？
答：
上述实验证实，对于理想气体，自由膨胀不对外做功，温度又不变，所以内能没变化。对于固定数量的气体分子来说，U由P、V、T中的两个独立变量确定，分别以T和V、T和p写成全微分的形式，比如\( \mathrm{d} U=\left(\frac{\partial U}{\partial T}\right)_{V} \mathrm{d} T+\left(\frac{\partial U}{\partial V}\right)_{T} \mathrm{d} V\)，总之，最后可以得到温度不变的时候，U对p或者V的偏导数都是0，所以得到的结论是，内能只是温度的函数，与体积和压力无关。
        对于实际气体，由于存在分子间作用力，所以内能与温度和体积有关（PVT三个中，只有两个独立变量）。

12.  理想气体，焓和温度的关系?
答：和11中类似，选取等温的情况，把焓全微分展开，也可以得到理想气体，焓只和温度有关。另外，根据热容的定义可以知道，等压和等体积热容都仅是温度的函数。

13. 等压热容和等体积热容的关系？
答： 通过较为复杂的数学推导，可以得到
\(C_{p}-C_{V}=n R \)