电磁场的守恒定律和对称性
电磁场是一种物质存在,具有能量、动量以及角动量。[mathjax]
分析如下:
1. 远处有源电荷(电流)激发整个空间产生电磁场,那么空间中的一个带电体会受到电场作用力,开始加速运动,动能增加;同时运动的带电体,在空间中形成电流,那么就会受到磁场的作用,使得运动方向偏转,动量发生变化,动能不变。 注:关掉电源,空间的电磁场不会立刻消失,仍然具有给带电体做功,以及改变其动量的能力,这证明带电体的能量/动量不是由源电荷/电流直接提供的,而是由电磁场提供的。
注:关掉电源,空间的电磁场不会立刻消失,仍然具有给带电体做功,以及改变其动量的能力,这证明带电体的能量/动量不是由源电荷/电流直接提供的,而是由电磁场提供的。
2. 考虑电荷/电流在建立电磁场时的能量/动量变化。将散落到无穷远的电荷一个个准静态地搬到一起,搬第一个不需要外力,但是后面的电荷都需要克服电场阻力,因此一直都需要外力不断地做功。电场建立完毕之后,先前的那些功就都转化成了电磁场的能量!动量也是一样的argument。
电磁学中,我们知道电容器中静电场的总能为\( \equiv U_{E}=\frac{1}{2} C V^{2} \),电感中的静磁场的总能为\( U_{B}=\frac{1}{2} L I^{2} \)。然而这样的推导不能告诉我们局域场的能量密度,我们用这两个公式得到的能量密度只是通过相当不严格的类比。
真空中电磁场的能量守恒定律
电磁场“看到”的不是物质,而是物质身上的电荷/电流,场对一块物质的作用力是通过对其电荷/电流作用实现的。我们先研究电荷,磁场对电荷不做功,只是改变动量,电场对电荷做功。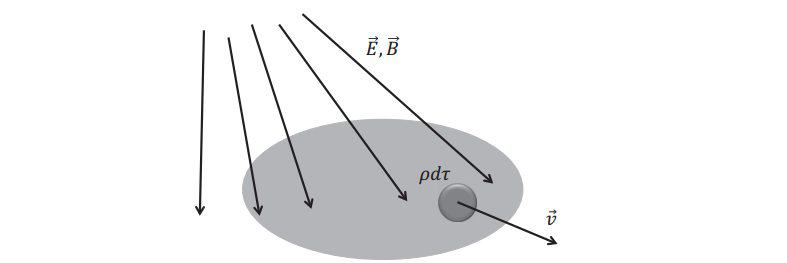 场在\( dt \)时间内,对\( \rho d \tau\)所做的功为$$\frac{d R}{d t}=\int \vec{E} \cdot \vec{j} d \tau$$ 场对带电体做功增加了带电体的机械能 \(W_{m} \),故$$\frac{d W_{m}}{d t}=\int \vec{E} \cdot \vec{j} d \tau$$变换一下麦克斯韦方程组第四个式子$$\vec{j}=\frac{1}{\mu_{0}} \nabla \times \vec{B}-\varepsilon_{0} \frac{\partial \vec{E}}{\partial t}$$,于是有$$\vec{j} \cdot \vec{E}=\frac{1}{\mu_{0}}(\nabla \times \vec{B}) \cdot \vec{E}-\frac{\varepsilon_{0}}{2} \frac{\partial}{\partial t} E^{2}$$将等式右边改写成对空间、时间的全微分形式,先根据\( \nabla \cdot(\vec{B} \times \vec{E})=\vec{E} \cdot(\nabla \times \vec{B})-\vec{B} \cdot(\nabla \times \vec{E})\)有$$\vec{j} \cdot \vec{E}=\frac{1}{\mu_{0}} \nabla \cdot(\vec{B} \times \vec{E})+\frac{1}{\mu_{0}} \vec{B} \cdot(\nabla \times \vec{E})-\frac{\varepsilon_{0}}{2} \frac{\partial}{\partial t} E^{2}$$而其中的第二\( \nabla \times \vec{E}=-\frac{\partial \vec{B}}{\partial t} \)于是整个改写为$$\vec{j} \cdot \vec{E}=-\frac{1}{\mu_{0}} \nabla \cdot(\vec{E} \times \vec{B})-\frac{1}{2} \frac{\partial}{\partial t}\left(\varepsilon_{0} E^{2}+\frac{1}{\mu_{0}} B^{2}\right)$$令$$\begin{aligned} \vec{S}_{P}(\vec{r}, t) &=\frac{1}{\mu_{0}} \vec{E} \times \vec{B}=\vec{E} \times \vec{H} \\ u(\vec{r}, t) &=\frac{1}{2}\left(\varepsilon_{0} E^{2}+\frac{1}{\mu_{0}} B^{2}\right) \end{aligned}$$于是$$\begin{aligned} \frac{d W_{m}}{d t} &=-\int \nabla \cdot \vec{S}_{P} d \tau-\frac{\partial}{\partial t} \int u d \tau \\ &=-\oint \vec{S}_{P} \cdot d \vec{S}-\frac{\partial}{\partial t} \int u d \tau \end{aligned}$$进一步改写$$\frac{d}{d t}\left[W_{m}+\int u d \tau\right]=-\oint \vec{S}_{P} \cdot d \vec{S}$$现在等式的物理意义非常明晰了。等式右边的负号表示的是能流是从外面穿过微小体积的表面进入的,那么能流的方向和面积矢量的方向是相反的,因此有个负号(\( \vec{S}_{P}\)和\(d \vec{S} \)的乘积是负数),或者我们可以理解为这个微小体积的表面是返现包裹空间的源,\( \vec{S}_{P}(\vec{r}, t)\)为能流密度,叫作坡印廷矢量。等式左边是时间的导数,其中的\( W_{m} \)是空间里物质的机械能量,而\( u(\vec{r}, t) \)描述的是这个位置此刻电磁场的能量密度。
场在\( dt \)时间内,对\( \rho d \tau\)所做的功为$$\frac{d R}{d t}=\int \vec{E} \cdot \vec{j} d \tau$$ 场对带电体做功增加了带电体的机械能 \(W_{m} \),故$$\frac{d W_{m}}{d t}=\int \vec{E} \cdot \vec{j} d \tau$$变换一下麦克斯韦方程组第四个式子$$\vec{j}=\frac{1}{\mu_{0}} \nabla \times \vec{B}-\varepsilon_{0} \frac{\partial \vec{E}}{\partial t}$$,于是有$$\vec{j} \cdot \vec{E}=\frac{1}{\mu_{0}}(\nabla \times \vec{B}) \cdot \vec{E}-\frac{\varepsilon_{0}}{2} \frac{\partial}{\partial t} E^{2}$$将等式右边改写成对空间、时间的全微分形式,先根据\( \nabla \cdot(\vec{B} \times \vec{E})=\vec{E} \cdot(\nabla \times \vec{B})-\vec{B} \cdot(\nabla \times \vec{E})\)有$$\vec{j} \cdot \vec{E}=\frac{1}{\mu_{0}} \nabla \cdot(\vec{B} \times \vec{E})+\frac{1}{\mu_{0}} \vec{B} \cdot(\nabla \times \vec{E})-\frac{\varepsilon_{0}}{2} \frac{\partial}{\partial t} E^{2}$$而其中的第二\( \nabla \times \vec{E}=-\frac{\partial \vec{B}}{\partial t} \)于是整个改写为$$\vec{j} \cdot \vec{E}=-\frac{1}{\mu_{0}} \nabla \cdot(\vec{E} \times \vec{B})-\frac{1}{2} \frac{\partial}{\partial t}\left(\varepsilon_{0} E^{2}+\frac{1}{\mu_{0}} B^{2}\right)$$令$$\begin{aligned} \vec{S}_{P}(\vec{r}, t) &=\frac{1}{\mu_{0}} \vec{E} \times \vec{B}=\vec{E} \times \vec{H} \\ u(\vec{r}, t) &=\frac{1}{2}\left(\varepsilon_{0} E^{2}+\frac{1}{\mu_{0}} B^{2}\right) \end{aligned}$$于是$$\begin{aligned} \frac{d W_{m}}{d t} &=-\int \nabla \cdot \vec{S}_{P} d \tau-\frac{\partial}{\partial t} \int u d \tau \\ &=-\oint \vec{S}_{P} \cdot d \vec{S}-\frac{\partial}{\partial t} \int u d \tau \end{aligned}$$进一步改写$$\frac{d}{d t}\left[W_{m}+\int u d \tau\right]=-\oint \vec{S}_{P} \cdot d \vec{S}$$现在等式的物理意义非常明晰了。等式右边的负号表示的是能流是从外面穿过微小体积的表面进入的,那么能流的方向和面积矢量的方向是相反的,因此有个负号(\( \vec{S}_{P}\)和\(d \vec{S} \)的乘积是负数),或者我们可以理解为这个微小体积的表面是返现包裹空间的源,\( \vec{S}_{P}(\vec{r}, t)\)为能流密度,叫作坡印廷矢量。等式左边是时间的导数,其中的\( W_{m} \)是空间里物质的机械能量,而\( u(\vec{r}, t) \)描述的是这个位置此刻电磁场的能量密度。
讨论:
(1) 当坡印廷矢量为零,即没有外界能量输入的情况下,机械能和电磁场能之间可以相互转化;
(2) 如果我们研究的一块区域没有源(电荷/电流),那么机械能\( W_{m}=0 \),于是有$$\nabla \cdot \vec{S}_{P}(\vec{r}, t)+\frac{\partial}{\partial t} u(\vec{r}, t)=0$$表面,外界坡印廷矢量输入的能量全部变成了该处的电磁场能,这和电荷守恒的连续性方程完全一样,又一次说明了电磁场是一种物质。
例子: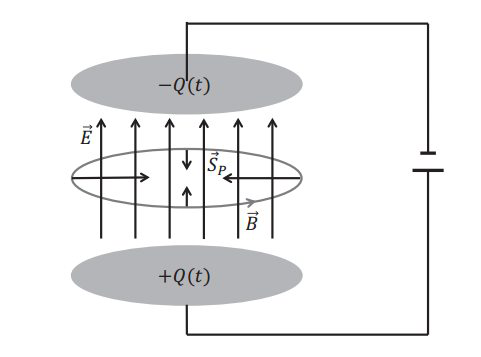 电场为\(E(t)=\frac{Q(t)}{\pi r^{2} \varepsilon_{0}} \),电容器的总能量为$$W=\frac{1}{2} \varepsilon_{0} E^{2} \cdot \Omega$$其中\( \Omega=\pi r^{2} h \)为电容器的体积。在充电过程中\(E \)缓慢变化,设\( \vec{E}=E(t) \vec{e}_{z} \),那么由第四个麦方程知,变化的电场会产生位移电流从而进一步产生磁场:$$\oint \vec{B} \cdot d \vec{l}=\mu_{0} \varepsilon_{0} \int_{S} \frac{\partial \vec{E}}{\partial t} \cdot d \vec{S}$$为了计算上式,采用柱坐标系得到电容器内的磁场为$$\vec{B}=\frac{1}{2 \pi \rho} \mu_{0} \varepsilon_{0} \pi \rho^{2} \frac{\partial E}{\partial t} \vec{e}_{\phi}$$磁场方向是顺时针,磁场的旋度方向正好的电场的方向。有了电场,又有了磁场,那么就有了能流密度矢量$$\vec{S}_{P}=\frac{1}{\mu_{0}} \vec{E} \times \vec{B}=\frac{\varepsilon_{0}}{2} E \frac{\partial E}{\partial t} \rho\left(-\vec{e}_{\rho}\right)$$右手螺旋法则知道二者叉乘的方向指向电容器中心轴线。对电容器侧面积分则得流入电容器的能量为$$\int \vec{S}_{P} \cdot d \vec{S}=\frac{\varepsilon_{0}}{2} E \frac{\partial E}{\partial t} r \cdot 2 \pi r h=\pi r^{2} h \varepsilon_{0} E \frac{\partial E}{\partial t}=\frac{\partial}{\partial t} W_{e, m}$$其中\( W=\frac{1}{2} \varepsilon_{0} E^{2} \cdot \Omega\)即为电场的能量。 它正好等于电容器中能量的增加率。这说明能量不是从导线中流过来的,而是从电容器外面的空间中通过电容器侧面流进电容器的。显然,通常认为能量是从导线中流过来的直觉是错误的 。
电场为\(E(t)=\frac{Q(t)}{\pi r^{2} \varepsilon_{0}} \),电容器的总能量为$$W=\frac{1}{2} \varepsilon_{0} E^{2} \cdot \Omega$$其中\( \Omega=\pi r^{2} h \)为电容器的体积。在充电过程中\(E \)缓慢变化,设\( \vec{E}=E(t) \vec{e}_{z} \),那么由第四个麦方程知,变化的电场会产生位移电流从而进一步产生磁场:$$\oint \vec{B} \cdot d \vec{l}=\mu_{0} \varepsilon_{0} \int_{S} \frac{\partial \vec{E}}{\partial t} \cdot d \vec{S}$$为了计算上式,采用柱坐标系得到电容器内的磁场为$$\vec{B}=\frac{1}{2 \pi \rho} \mu_{0} \varepsilon_{0} \pi \rho^{2} \frac{\partial E}{\partial t} \vec{e}_{\phi}$$磁场方向是顺时针,磁场的旋度方向正好的电场的方向。有了电场,又有了磁场,那么就有了能流密度矢量$$\vec{S}_{P}=\frac{1}{\mu_{0}} \vec{E} \times \vec{B}=\frac{\varepsilon_{0}}{2} E \frac{\partial E}{\partial t} \rho\left(-\vec{e}_{\rho}\right)$$右手螺旋法则知道二者叉乘的方向指向电容器中心轴线。对电容器侧面积分则得流入电容器的能量为$$\int \vec{S}_{P} \cdot d \vec{S}=\frac{\varepsilon_{0}}{2} E \frac{\partial E}{\partial t} r \cdot 2 \pi r h=\pi r^{2} h \varepsilon_{0} E \frac{\partial E}{\partial t}=\frac{\partial}{\partial t} W_{e, m}$$其中\( W=\frac{1}{2} \varepsilon_{0} E^{2} \cdot \Omega\)即为电场的能量。 它正好等于电容器中能量的增加率。这说明能量不是从导线中流过来的,而是从电容器外面的空间中通过电容器侧面流进电容器的。显然,通常认为能量是从导线中流过来的直觉是错误的 。
注:
(1) 能量不是依附于电荷而存在的,因为场本身是可以脱离电荷而存在的。充电过程中,电场变化导致的位移电流,补充真实电流,从而产生磁场。磁场一旦出现,就在空间产生能流,可以将能量一点点搬运过来。
(2) 忽略了弛豫效应/边缘效应,弛豫非常快,充电非常慢。电容器中能量,不是通过导线由电荷流过来的,而是在空间通过电力线的变化,以能流的方式从电容的侧面进入的。 显然,通常认为能量是从导线中流过来的直觉是错误的 。思考为什么,证据?
(3) 柱坐标回顾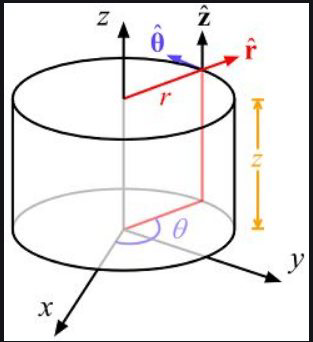
电磁场的动量守恒定律
力只是一个中间过程,不是一个fundamental的物理量,真正fundamental的物理量是一些守恒量,比如力对应动量,功对应能量,力矩对应角动量。动量、能量、角动量等才是fundamental的。
带电体受到洛伦兹力,则其机械动量的变化率为$$\frac{d G_{m}}{d t}=\int(\rho d \tau \vec{E}+\rho d \tau \vec{v} \times \vec{B})=\int(\rho \vec{E}+\vec{j} \times \vec{B}) d \tau=\int \vec{f} d \tau$$用场方程把\( \rho\)和\( \vec{j}\)消去,力密度改写为$$\vec{f}=\varepsilon_{0}(\nabla \cdot \vec{E}) \vec{E}+\frac{1}{\mu_{0}}\left(\nabla \times \vec{B}-\mu_{0} \varepsilon_{0} \frac{\partial \vec{E}}{\partial t}\right) \times \vec{B}$$按照先前的方法,我们希望将上面的式子改写成对空间、时间的全微分,先考虑时间部分,配分得$$-\varepsilon_{0} \frac{\partial \vec{E}}{\partial t} \times \vec{B}=-\varepsilon_{0} \frac{\partial}{\partial t}(\vec{E} \times \vec{B})+\varepsilon_{0} \vec{E} \times \frac{\partial \vec{B}}{\partial t}=-\varepsilon_{0} \frac{\partial}{\partial t}(\vec{E} \times \vec{B})-\varepsilon_{0} \vec{E} \times(\nabla \times \vec{E})$$那么接下来分两个部分考虑:
(1) 考虑\( \vec{f}\)中所有包含电场\( \vec{E} \)的项得到$$\begin{aligned} (\nabla \cdot \vec{E}) \vec{E}-\vec{E} \times(\nabla \times \vec{E}) &=(\nabla \cdot \vec{E}) \vec{E}-\left[\frac{1}{2} \nabla(\vec{E} \cdot \vec{E})-(\vec{E} \cdot \nabla) \vec{E}\right] \\ &=\nabla \cdot(\vec{E} \vec{E})-\nabla\left(\frac{1}{2} E^{2}\right) \\ &=\nabla \cdot(\vec{E} \vec{E})-\nabla \cdot\left(\frac{1}{2} E^{2} \vec{I}\right) \end{aligned}$$这其中运用到了并矢的计算公式$$\nabla \cdot(\overrightarrow{A B})=(\nabla \cdot \vec{A}) \vec{B}+(\vec{A} \cdot \nabla) \vec{B}$$以及势函数的梯度场等于一个二阶张量(单位张量\( \stackrel{\leftrightarrow}{I}\))通过求散度降阶$$\nabla \varphi=\nabla \cdot(\varphi \stackrel{\leftrightarrow}{I})$$注:上面两个公式的证明
(1) \(\nabla \varphi=\nabla \cdot(\varphi \stackrel{\leftrightarrow}{I}) \);
(2) \( \nabla \cdot(\varphi \stackrel{\leftrightarrow}{I})=\partial_{i}(\varphi \stackrel{\leftrightarrow}{I})_{i j} \hat{e}_{j}=\partial_{i}\left(\varphi \delta_{i j}\right) \hat{e}_{j}=\partial_{i}(\varphi) \hat{e}_{i}=\nabla \varphi\)
(3) 关于张量可以参考-电动力学-张量补充
(2) 考虑磁场项\( \frac{1}{\mu_{0}}(\nabla \times \vec{B}) \times \vec{B}\),和电场类比,加上一个零项\( \frac{1}{\mu_{0}}(\nabla \cdot \vec{B}) \vec{B}\),得到与磁场有关的项为$$(\nabla \cdot \vec{B}) \vec{B}+(\nabla \times \vec{B}) \times \vec{B}=\nabla \cdot(\vec{B} \vec{B})-\nabla \cdot\left(\frac{1}{2} B^{2} \vec{I}\right)$$因此$$\vec{f}=-\nabla \cdot \stackrel{\leftrightarrow}{T}-\frac{\partial}{\partial t} \vec{g}$$其中$$\begin{array}{c}
\stackrel{\leftrightarrow}{T}=\frac{1}{2}\left(\varepsilon_{0} E^{2}+\frac{1}{\mu_{0}} B^{2}\right) \stackrel{\leftrightarrow}{I}-\varepsilon_{0} \vec{E} \vec{E}-\frac{1}{\mu_{0}} \vec{B} \vec{B} \\
\vec{g}=\varepsilon_{0}(\vec{E} \times \vec{B})=\frac{1}{c^{2}} \vec{S}_{P}
\end{array}$$于是机械动量随时间的变化率为$$\frac{d \vec{G}_{m}}{d t}=-\oint d \vec{S} \cdot \stackrel{\leftrightarrow}{T}-\frac{d}{d t} \int \vec{g} d \tau$$完全类似对电磁能量的讨论,\( \vec{g} \)就是电磁场的动量密度,因为动量本身是一个矢量,所以动量密度也必须是矢量,动量流密度(矢量流密度)就必须是一个二阶张量,即\( \stackrel{\leftrightarrow}{T} \)(张量,并矢)。对每个动量分量(以\( x \)方向为例),上式可以改写成$$\frac{d G_{m}^{x}}{d t}=-\oint d \vec{S} \cdot \vec{T}_{x}-\frac{d}{d t} \int g_{x} d \tau$$\( \vec{T}_{x}\)是一个标量,上式就成了一个和能量流类似的东西。而$$\vec{G}_{e, m}=\int_{\Delta \Omega} \varepsilon_{0}(\vec{E} \times \vec{B}) d \tau$$这就是\( \Delta \Omega \)体积内电磁场所具携带的总能量。
注:
(1) 根据公式,可知动量必须有磁场存在;
(2) 上面有动量密度和能流密度之间的关系\( \vec{g}=\frac{1}{c^{2}} \vec{S}_{P} \),而能流密度其实是能量密度\( u\)乘以速度\( c \),于是动量密度\( \vec{g}=\frac{u}{c} \),即$$u=\vec{g}c$$动量密度乘以光速等于能量密度,能量密度乘以光速等于能量流密度。
电磁场对闭合区域内的带电体的作用总力可以表示为$$\vec{F}_{e m}=\frac{\partial \vec{G}_{m}}{\partial t}==-\oint_{S} d \vec{S} \cdot \stackrel{\leftrightarrow}{T}-\int_{V} \frac{\partial}{\partial t} \vec{g} d \tau$$讨论:
(1) 等式右边第一项\(-\oint_{S} d \vec{S} \cdot \stackrel{\leftrightarrow}{T} \)表示电磁场在单位时间内通过界面从外面传递到曲面内部的总的动量。根据力的定义,这就是外面的电磁场通过界面给闭合区域内的物质施加的总力。如弹性力学中的张力一样,\( -\vec{e}_{n} \cdot \stackrel{\leftrightarrow}{T}\)表示单位时间内\( dS \)区域受到的力(类似应力,或者压强的概念),\(\stackrel{\leftrightarrow}{T} \)为麦克斯韦应力张量。可以形象地把电磁场想象成一个网,网格之间有张力,网中间放置一个钢球,即我们考虑的物质。对网施加扰动,则动量通过界面“流入”闭合区域,一部分变成了区域内部的网的动量,另一部分传递给钢球,给钢球施加了作用力。也可将电磁场想象成水,水中有一钢球,取一闭合界面,则外面的水物质一直对立面的水施加压力。 (2) 然而这些“总力”不见得都作用到区域内的物质上,还作用到区域内的电磁场上,引发区域内的电磁场的动量的增加。等式右边第二项就是减去这部分的消耗。
(2) 然而这些“总力”不见得都作用到区域内的物质上,还作用到区域内的电磁场上,引发区域内的电磁场的动量的增加。等式右边第二项就是减去这部分的消耗。
(3) 在稳态或时场随时间谐变的情况下,2中提到的消耗部分为零或者说时间上的平均为零。此时物质在电磁场中的受力完全由麦克斯韦张量和面积的积分来决定。小心设计一些特定的电磁场结构,比如一束高斯型光束,处于光场之中的介质小球就会受到力的作用,其在光场中受“光力”会产生移动最终到达平衡位置。因此我们可以通过改变光束的位置来有效地移动小球,这就是“光学镊子”(Optical Tweezers)的基本工作原理。
例子:用牛刀杀鸡(忽略边缘效应,求面积为A的板子的受力)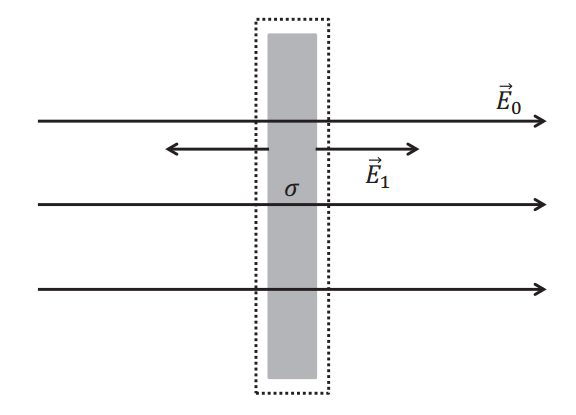 解:空间中的总场为$$\vec{E}_{r i g h t}=\vec{E}_{0}+\frac{\sigma}{2 \varepsilon_{0}} \hat{e}_{x} \quad \vec{E}_{l e f t}=\vec{E}_{0}-\frac{\sigma}{2 \varepsilon_{0}} \hat{e}_{x}$$则麦克斯韦张量为$$\begin{aligned}
解:空间中的总场为$$\vec{E}_{r i g h t}=\vec{E}_{0}+\frac{\sigma}{2 \varepsilon_{0}} \hat{e}_{x} \quad \vec{E}_{l e f t}=\vec{E}_{0}-\frac{\sigma}{2 \varepsilon_{0}} \hat{e}_{x}$$则麦克斯韦张量为$$\begin{aligned}
\stackrel{\leftrightarrow}{T} &=\frac{1}{2} \varepsilon_{0} E^{2} \stackrel{\leftrightarrow}{I}-\varepsilon_{0} \vec{E} \vec{E} \\
&=\frac{1}{2} \varepsilon_{0} E^{2}(\hat{x} \hat{x}+\hat{y} \hat{y}+\hat{z} \hat{z})-\varepsilon_{0} E^{2} \hat{x} \hat{x} \\
&=-\frac{1}{2} \varepsilon_{0} E^{2} \hat{x} \hat{x}+\frac{1}{2} \varepsilon_{0} E^{2}(\hat{y} \hat{y}+\hat{z} \hat{z})
\end{aligned}$$作一闭合曲面,求电磁场对物质的力$$\begin{aligned} \vec{F} &=-\oint \vec{n} \cdot \stackrel{\leftrightarrow}{T} d S \\ &=-A \hat{x} \cdot\left[\stackrel{\leftrightarrow}{T}_{r i g h t}-\stackrel{\leftrightarrow}{T}_{l e f t}\right] \\ &=A \hat{x} \frac{1}{2} \varepsilon_{0}\left[E_{r i g h t}^{2}-E_{l e f t}^{2}\right] \\ &=A \hat{x} \frac{1}{2} \varepsilon_{0} 4 \cdot E_{0} \cdot \frac{\sigma}{2 \varepsilon_{0}} \\ &=\hat{x} E_{0} \cdot Q \end{aligned}$$注:(1) 因为没有磁场项,所以麦克斯韦张量表达式比较简单,而电磁场的动量密度直接为零。
(2) 这里用牛刀比较麻烦,但是如果电磁场不是均匀的,或者板子的形状无规则那么就必须要这个牛刀了。
(3) 电磁场中,只有磁场或者只有电场,都存在电磁场能量密度;但是对动量密度来说,必须电场和磁场都同时存在。
(4) 现代科学摒弃了牛顿力学中牛“力”、“功”、“力矩”的概念,因为它们不本质,一般情况下难以定义。取而代之的是“动量”、“能量”,“角动量”等更本质的概念。
受力 = 能量的变化;
受力矩 = 角动量的变化;
做功 = 能量变化;
例子:求解质量为\( m\),带电量为\( q\)的粒子在稳定磁场中的运动,试求带电粒子在磁场中的总动量。 解:带电粒子使得空间存在电场,这样电场和磁场都有了,那么电磁场就会有动量,但与电荷存在于磁场中这个事实有关,因此通常算到电荷的总动量里。电磁场的动量为:$$\vec{G}_{e, m}=\int_{V} \varepsilon_{0}(\vec{E} \times \vec{B}) d \tau^{\prime}=\int_{V} \varepsilon_{0} \vec{E} \times(\nabla \times \vec{A}) d \tau^{\prime}$$当运动电荷的速度远小于光速时,可以近似认为运动的电荷只产生电场,其产生的磁场可以忽略,因此有$$\nabla \times \vec{E}=0 \quad \nabla \cdot \vec{E}=\varepsilon_{0} q \delta(\vec{r}-\vec{v} d t)$$而空间的磁场完全由稳定的外磁场贡献,因此有$$\nabla \cdot \vec{A}=0$$把它代人上式后,注意到第一项对空间的积分可以转化成在中括号里面 的场在无穷远处表面的面积分,当电流分布在空间有限区域中时,这一 项= 0。我们得到$$\vec{G}_{e, m}=\int q \vec{A} \delta(\vec{r}-\vec{v} t) d \tau^{\prime}=q \vec{A}(\vec{v} t)$$ 由此我们可以得到带电的运动粒子在外磁场中的总动量为$$\vec{p}=m \vec{v}+q \vec{A}$$ \( m \vec{v} \)是带电粒子的机械动量,而\( q \vec{A} \)是电荷与外场拥有的“附加”(相互作用)电磁动量,\( \vec{p} \)是总动量,又叫作正则动量。
解:带电粒子使得空间存在电场,这样电场和磁场都有了,那么电磁场就会有动量,但与电荷存在于磁场中这个事实有关,因此通常算到电荷的总动量里。电磁场的动量为:$$\vec{G}_{e, m}=\int_{V} \varepsilon_{0}(\vec{E} \times \vec{B}) d \tau^{\prime}=\int_{V} \varepsilon_{0} \vec{E} \times(\nabla \times \vec{A}) d \tau^{\prime}$$当运动电荷的速度远小于光速时,可以近似认为运动的电荷只产生电场,其产生的磁场可以忽略,因此有$$\nabla \times \vec{E}=0 \quad \nabla \cdot \vec{E}=\varepsilon_{0} q \delta(\vec{r}-\vec{v} d t)$$而空间的磁场完全由稳定的外磁场贡献,因此有$$\nabla \cdot \vec{A}=0$$把它代人上式后,注意到第一项对空间的积分可以转化成在中括号里面 的场在无穷远处表面的面积分,当电流分布在空间有限区域中时,这一 项= 0。我们得到$$\vec{G}_{e, m}=\int q \vec{A} \delta(\vec{r}-\vec{v} t) d \tau^{\prime}=q \vec{A}(\vec{v} t)$$ 由此我们可以得到带电的运动粒子在外磁场中的总动量为$$\vec{p}=m \vec{v}+q \vec{A}$$ \( m \vec{v} \)是带电粒子的机械动量,而\( q \vec{A} \)是电荷与外场拥有的“附加”(相互作用)电磁动量,\( \vec{p} \)是总动量,又叫作正则动量。
讨论:
(1) \( q \vec{A}\) 前面的\( q\)产生电场,后面的\( \vec{A} \)产生磁场,二者组合在一起才有了附加电磁动量;
(2) \( q \vec{A}\) 即不属于电荷本身的机械能量,也不属于原来的磁场,而是二者相互作用引起的,不是其中任何单一一方的贡献,单一存在的时候也不存在这一动量。类似一个巴掌拍不响;
(3) 这个结果是在低速情况下得到的;
(4) 如何理解这个相互作用引起的“附加动量”?可以考虑建立这个状态的过程,一开始电荷处于无穷远处,没有电磁场动量;当电荷靠近时,线圈与运动电荷之间有相互作用力,要达到最终的状态,必须有外力的输入。因此,在此过程中一直有外力对体系(线圈+电荷)输入动量(冲量),这部分动量被储存在体系中作为电荷的附加动量。类比电势能(无穷远处移过来一个电荷,要克服电场力,做功,做的功以势能的形式存储在电势场和电荷整个体系中)。
(5) \( \vec{p}\)是总动量,对例子的运动量子化后其对应的算符为\( \vec{p} \rightarrow -i \hbar \nabla\)。然而磁场不对带电粒子做功,因此带电粒子的动能依然是\( \frac{1}{2 m}(m|\vec{v}|)^{2}=\frac{1}{2 m}(\vec{p}-q \vec{A})^{2} \),写成算符的形式为\( \frac{1}{2 m}(-i \hbar \nabla-q \vec{A})^{2}\)。