图床 Physics-img/
物理思想进课堂专题
一份线上物理系本科层次的自学指南

S. Weinberg的四点忠告：
(1) 没有人了解所有的知识，你也不必。
(2) 学会游泳而不下沉后，应该到波涛汹涌的地方去。
(3) 要原谅自己虚掷时光。
(4) 学一点科学史，起码你所研究的学科的历史。

“如果你想学习某个东西，就去给别人上这门课。”——约翰·惠勒(John A. Wheeler)

物理学家网站：

冯元平(NUS)

物理科普网站：

• Radioactivity科普网站
• 太空中的温度为零下270摄氏度，为什么空间站反而要增加散热？

 

物理教育

现象是物理学的根源。什么是物理学？物理学是研究物质、能量和它们的相互作用的学科。

赵凯华：物理学代表着一套获得知识、组织知识和运用知识的有效步骤和方法。把这套方法运用到什么问题上，这问题就变成了物理学。

物理学的领域：
(1) 空间尺度($41$个数量级)，${10}^{-15}$ m(fm，质子半径)到${10}^{26}$ m(目前可探测到的最远类星体的距离)。
(2) 时间尺度(64个数量级)，${10}^{-25}$ s(最不稳定粒子的寿命)到${10}^{39}$ s(质子的寿命)。

下图是著名的“物理学大蟒”，天体物理和粒子物理两大尖端紧密衔接(天体量子力学，或者叫天体粒子物理)，这么大和这么小是怎么衔接的呢？这就是物理学对自然界的统一的描述和理解，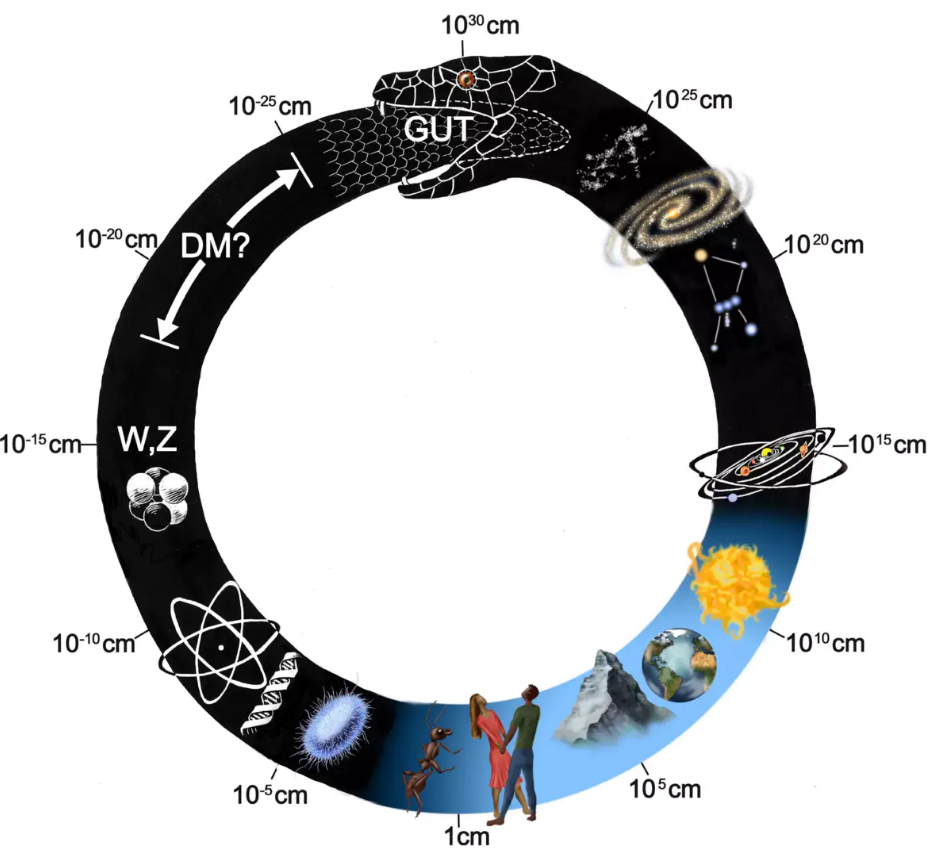

物理学的分支
(1) 按基础性和建立的历史分类：牛顿力学，热力学和统计物理，电磁学相对论，量子力学，量子场论……(教材的分类)
(2) 按物质的层次和状态分类粒子，原子核，凝聚态，原子分子，等离子体，引力和宇宙学，宇宙射线……

物理学的发展
(1) 牛顿力学研究弱引力场中物体的低速作用；物理学和哲学的剥离就是从牛顿力学开始的。
(2) 狭义相对论1905年由爱因斯坦发表，把力学扩展到高速、高能领情形；
(3) 广义相对论1916年由爱因斯坦发表，包括了加速参考系，是普适的引力理论。牛顿的万有引力理论只是其弱引力极限。

以上都是经典力学。上面三种力学都没有涉及到量子的概念，所以都可以叫作经典力学，只是狭义相对论和广义相对论是近代的经典力学。

经典力学在以往被认为是决定论的，但在上世纪60年代，由于计算机的应用，人们发现经典力学的实际问题大部分是非决定论的，具有不可预测性，也即——混沌。(比如小混沌摆)动力学方程是非线性的系统，称为非线性的系统。非线性的系统往往是非决定论的。

混沌现象和热力学中的随机现象不一样，它是内在的随机性(由动力学方程决定的，非线性系统)，是决定性的混乱。另外混沌现象的演技也是由于计算机的应用而导致的，因为之前一直觉得是计算不够精确，但是后面即使有了相当精确的计算机也无法预测混沌现象。

近代物理学的核心：相对论、量子力学。
如何理解量子力学的基本概念、基本图像和基本规律，一直存在着深刻的、剧烈的争论。矩阵力学和波动力学是对量子力学的等价描述。

现象是物理学的根源：杨振宁：很多学生在学习中形成一种印象，以为物理学就是一些演算。也算是物理学的一部分，但不是最重要的部分，物理学最重要的部分是与现象有关的。绝大部分物理学是从现象中来的。现象是物理学的根源。

电子驻波简正模式——建立量子论的启发(圓周上的駐波及对应的展示工具)

注：驻波standing wave为两个波长、周期、频率和波速皆相同的正弦波相向行进干涉而成的合成波。与行波不同，驻波的波形无法前进，因此无法传播能量，故名之。

费曼理想中的教材：

• 兼顾两头；
• 蔑视用字解释字，物理学家的思考方式；
• 教材中缺乏实验的分析；
• 请给我一个例子；
• 不停下来思考，我们的教学目的是什么？
• 应该有反馈环节；
• 相关性、类比性、思想实验

学习学：
(1) 巴比伦方法：从具体例子入手；
(2) 希腊方法：从概念到归纳；
(3) 费曼方法：相关性、类比性、思想实验。

参考资料：
(1) 从“学会已知”到“探索未知”——物理思想进课堂专栏年度回顾与展望
(2) 清华大学-安宇老师的大学物理视频
(3) 费曼谈巴西的物理教育
(4) 费曼谈草包族科学

 

 

物理教学中的几个概念

爱因斯坦扩散系数

一维布朗运动粒子位移平均方偏差与时间成正比$$⟨x^2⟩=2Dt$$$D$称为爱因斯坦扩散系数，这里为啥叫扩散系数?

朗之万理论，$F-\gamma \dot{x}=M\ddot{x}$，弛豫时间$\tau ={\displaystyle \frac{M}{\gamma }}$，布朗粒子一开始静止。
方均偏离：$$⟨x^2⟩=\frac{2kT}{M}{\tau }^2[\frac{t}{\tau }-(1-e^{-\frac{t}{\tau }})]$$(1) 当$t<<\tau$，是匀速运动$⟨x^2⟩={\displaystyle \frac{kT}{M}{t}^2=⟨v^2⟩t^2}$

(2) 当$t\gg \tau$时，是布朗运动$⟨x^2⟩={\displaystyle \frac{2kT}{\gamma }t=2Dt}$，布朗运动的动力就是热运动，这里的爱因斯坦扩散系数和热运动能量$kT$有关，和流体的阻力$\gamma$成反比，这是很合理的结论。

爱因斯坦布朗运动理论：和朗之万的理论不同，爱因斯坦研究布朗运动采用的是一维无规则行走的模型，对于一维规则行走来说，向前的概率为$p$，向后的概率为$q$，有$p=q=1/2$。如果迈了$N$步，那么其中向前$n$，向后$N-n$的概率是多少？

二项式分布计算：$P_N(n)=C_N^n{p}^n{q}^{N-n}$
偏差或涨落：$m=2n-N$净向前步数，$\overline{m}=0$，$\overline{m^2}=N$
平均步长$l$，迈一步平均时间${\tau }^{\ast }$，则时间$t$后步数$$N=\frac{t}{{\tau }^{\ast }}$$偏移距离：$x=ml$
平均偏离：$⟨x⟩=0$
方均偏离：$⟨x^2⟩=\overline{m^2}{l}^2={\displaystyle \frac{l^2}{{\tau }^{\ast }}t}$
于是爱因斯坦扩散系数为$D={\displaystyle \frac{l^2}{2{\tau }^{\ast }}={\displaystyle \frac{kT}{\gamma }}}$，对应于朗之万模型。

爱因斯坦一维扩散理论：扩散等同于布朗运动或一维无规则行走。平均步长$l$，迈一步平均时间${\tau }^{\ast }$，开始有$n_0$个粒子在原点，$t$时刻$x$处粒子数目是多少？正比于此时此处的概率：$$n_0{C}_N^n/2^{N}m=2n-N{n}_0{C}_N^{(N+m)/2}/2^N$$二项分布：$$P_N(m)=\frac{N!}{(N+m)/2!(N-m)/2!}{\left(\frac{1}{2}\right)}^N$$$N$很大的时候有$\ln N!\approx N\ln {\displaystyle \frac{N}{e}+{\displaystyle \frac{1}{2}\ln (2\pi N)}}$ $$m\ll <N/2\ln P_N(m)\approx -\frac{m^2}{2N}+\frac{1}{2}\ln \frac{2}{\pi N}$$二项分布近似为高斯分布：$P_N(m)\approx {\left({\displaystyle \frac{2}{\pi N}}\right)}^{1/2}{e}^{-\frac{m^2}{2N}}$ $$N=\frac{t}{{\tau }^{\ast }}m=\frac{x}{l}D=\frac{l^2}{2{\tau }^{\ast }}$$扩散概率 $P(x)\approx {\left({\displaystyle \frac{1}{4\pi Dt}}\right)}^{1/2}{e}^{-\frac{x^2}{4Dt}}$
粒子数分布 $n(x)\approx n_0{\left({\displaystyle \frac{1}{4\pi Dt}}\right)}^{1/2}{e}^{-\frac{x^2}{4Dt}}$

一维扩散方程(开始有$n_0$个粒子在原点) $$\frac{\partial n}{\partial t}=D^{\ast }\frac{{\partial }^{2}n}{\partial x^2}$$一维扩散方程的解为$$n(x)=n_0{\left(\frac{1}{4\pi D^{\ast }t}\right)}^{1/2}{e}^{-\frac{x^2}{4D^{\ast }t}}$$ $D=D^{\ast }$ 爱因斯坦扩散系数

参考资料：
(1) 布朗运动是什么?太阳光到地球需要多久?—李永乐
(2) 世界杯球场上的诡异足球轨迹，如何用爱因斯坦的理论来解释？李永乐老师讲布朗运动
(3) 布朗运动理论及其在复杂气候系统研究中的应用—物理2022——孙昌璞

电磁波纵向分量

• 电磁波是横波，但是如果有纵波分量的话，光子质量不为零；
• 如果库伦作用偏离反平方率的话，光子质量不为零；
• 在超导体内，规范对称性被破坏，所以光子质量不为零；
• 质量与真空自发对称性破缺有关，所谓希格斯机制，这与本科教学比较远。

汤川秀树理论

汤川势$\varphi \propto {\displaystyle \frac{e^{-\mu r}}{r}}$

核子相互作用是短程的，指数衰减。

汤川势${\mathrm{\nabla }}^2\varphi -{\mu }^2\varphi =0$球对称解。

类比静电场${\mathrm{\nabla }}^2\varphi =0$球对称解$\varphi \propto {\displaystyle \frac{1}{r}}$

考虑时间变化的电磁场方程(是标量算符，洛伦兹规范)$$\begin{array}{c}{\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◻"\; src="https://s.w.org/images/core/emoji/15.0.3/svg/25fb.svg">}}^2\varphi =0\\ \mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◻"\; src="https://s.w.org/images/core/emoji/15.0.3/svg/25fb.svg">}{\overrightarrow{\mathrm{\nabla }}}^2-\frac{1}{c^2}\frac{{\partial }^2}{\partial t^2}\end{array}$$汤川强场方程$${\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◻"\; src="https://s.w.org/images/core/emoji/15.0.3/svg/25fb.svg">}}^2\varphi ={\mu }^2\varphi$$于是$${\overrightarrow{\mathrm{\nabla }}}^2\varphi -\frac{1}{c^2}\frac{{\partial }^2\varphi }{\partial t^2}={\mu }^2\varphi$$根据平面波$\varphi ={\varphi }_0{e}^{i(\omega t-kz)}$将方程${\displaystyle \frac{{\omega }^2}{c^2}-k^2-{\mu }^2=0}$都乘以${\hslash }^2$得到$$\frac{E^2}{c^2}-p^2={\mu }^2{\hslash }^2$$比较$E^2=p^2{c}^2+m^2{c}^4$
于是相当于场量子有质量$m={\displaystyle \frac{\hslash \mu }{c}}$核力力程$$\begin{array}{rl}& \varphi \propto \frac{e^{-\mu r}}{r}\\ \sim & {10}^{-14}-{10}^{-15}\mathrm{m}\mu \sim {10}^{14}-{10}^{15}{\mathrm{m}}^{-1}\end{array}$$“强场”量子，$\pi$介子质量$$\begin{array}{rl}& m=\mu \hslash /c\\ & m{c}^2\sim 100\mathrm{MeV}\end{array}$$$\mu$越小，对库仑反平方率偏离越小光子质量就越接近于零

纵波分量(假设电磁波向$z$方向传播)
电场强度$\overrightarrow{E}=E_x{\overrightarrow{e}}_x+\xi {\overrightarrow{e}}_z$
假设有一个很小的纵波分量$\xi$
磁场还是只有横波分量$\overrightarrow{B}=B_y{\overrightarrow{e}}_y$，这个时候考察纵波分量$\xi$对光子静止质量的贡献，要求满足$$\begin{array}{c}\mathrm{\nabla }\cdot \overrightarrow{E}=0\mathrm{\nabla }\cdot \overrightarrow{B}=0\\ \mathrm{\nabla }\times \overrightarrow{E}=-\frac{\partial \overrightarrow{B}}{\partial t}\mathrm{\nabla }\times \overrightarrow{B}=\frac{1}{c^2}\frac{\partial \overrightarrow{E}}{\partial t}\end{array}$$而且是沿着$z$向传播的波$$\begin{array}{rl}B=B_y(x,z-ut)E_x& =E_x(x,z-ut)\\ \xi & =\xi (x,z-ut)\end{array}$$带入得到$$\frac{\partial B_y}{\partial x}=\frac{1}{c^2}\frac{\partial \xi }{\partial t}\frac{\partial B_y}{\partial z}=-\frac{1}{c^2}\frac{\partial E_x}{\partial t}$$电磁波的磁场/电场必须满足波动方程，所以必须有$${\overrightarrow{\mathrm{\nabla }}}^2\overrightarrow{B}-\frac{1}{c^2}\frac{{\partial }^2\overrightarrow{B}}{\partial t^2}=0$$分立变量$B_y=\eta (x)e^{ik(z-ut)}$有$${\eta }^{\prime \prime }+k^2(\frac{u^2}{c^2}-1)\eta =0$$于是有波动解$$B_y=B_0{e}^{i(k_{x}x+\phi )}{e}^{ik(z-ut)}$$而$$k_x^2=k^2(\frac{u^2}{c^2}-1)u{u}_g=c^2$$同理有$$\begin{array}{rl}{E}_x& =E_0{e}^{i(k_{x}x+\phi )}{e}^{ik(z-ut)}\\ \xi & =-\delta e^{i(k_{x}x+\phi )}{e}^{ik(z-ut)}\end{array}$$因为要满足麦克斯韦方程组

满足麦克斯韦方程组$${\overrightarrow{\mathrm{\nabla }}}^2{B}_y-\frac{1}{c^2}\frac{{\partial }^2{B}_y}{\partial t^2}=0$$于是有$$\begin{array}{r}\to {\displaystyle \frac{{\partial }^2{B}_y}{\partial z^2}-{\displaystyle \frac{1}{c^2}{\displaystyle \frac{{\partial }^2{B}_y}{\partial t^2}=-{\displaystyle \frac{{\partial }^2{B}_y}{\partial x^2}}}}}\\ {\displaystyle \frac{{\partial }^2{B}_y}{\partial z^2}-{\displaystyle \frac{1}{c^2}{\displaystyle \frac{{\partial }^2{B}_y}{\partial t^2}=k_x^2{B}_y}}}\end{array}$$根据汤川理论，场量子质量$m={\displaystyle \frac{\hslash k_x}{c}}$，带入$k_x={\displaystyle \frac{\delta }{E_0}k}$得到$$m=\frac{\hslash k\delta }{c{E}_0}$$即场量子(光子)质量与纵波分量有关。

超导体内，规范对称性被破坏
London equation$${\overrightarrow{j}}_s+\frac{N{e}_s^2}{m_s}\overrightarrow{A}=0$$矢势$A$确定, 规范变换对称性没有了$$\mathrm{\nabla }\times \overrightarrow{H}={\overrightarrow{J}}_0+\frac{\partial \overrightarrow{D}}{\partial t}$$若$\tau \omega <<1$，超导电流>>通常电流，只考虑超导电流的话$$\begin{array}{rl}\mathrm{\nabla }\times \overrightarrow{H}& =-\frac{N{e}_s^2}{m_s}\overrightarrow{A}+\frac{\partial \overrightarrow{D}}{\partial t}\\ \mathrm{\nabla }\times \frac{\overrightarrow{B}}{{\mu }_0}& =-\frac{N{e}_s^2}{m_s}\overrightarrow{A}+{\epsilon }_0\frac{\partial \overrightarrow{E}}{\partial t}\end{array}$$整理一下$$\begin{array}{c}\mathrm{\nabla }\times (\mathrm{\nabla }\times \frac{\overrightarrow{B}}{{\mu }_0})=-\frac{N{e}_s^2}{m_s}\mathrm{\nabla }\times \overrightarrow{A}+{\epsilon }_0\mathrm{\nabla }\times \frac{\partial \overrightarrow{E}}{\partial t}\\ {\mathrm{\nabla }}^2\overrightarrow{B}-\frac{{\partial }^2\overrightarrow{B}}{c^2\partial t^2}=\frac{{\mu }_{0}N{e}_s^2}{m_s}\overrightarrow{B}\end{array}$$根据汤川理论，电磁场量子获得质量$$m=\frac{\hslash e_s}{c}\sqrt{\frac{{\mu }_{0}N}{m_s}}$$

相空间

简介

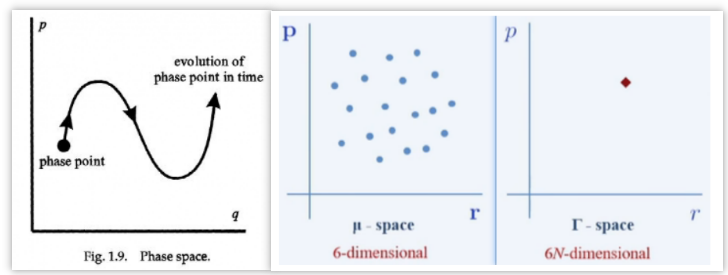
一个随时间演化的system，我们可以描述出它的运动轨迹，以及它在运动轨迹上任一点的速度，这样它的演化过程就被完全描述。classical mechanics随时间演化的过程中所处的每一个state也可以由系统的position和momentum来描述，或者更一般地来说是广义坐标和广义动量(比如单摆系统的角度和角动量)。相空间描述的好处是使我们的研究方法更一般化更简单化，更适合用来研究经典力学中系统的Lagrangian和Hamiltonian。

相空间中代表点的轨迹不相交。这一结论出发，可以很容易得到经典力学中的一个重要结论：相流不可压缩，即Liouville 定理，在初始时刻任意选取一块相体积(例如一个球)，在某个力学系统的演化方程的作用下，这个相体积的形状会变(例如拉扯为椭圆、矩形等)，但是体积是守恒的。

相空间其实就是从多个维度(自由度)去确定系统的运动状态，任何一个守恒量(方程)都可以降低系统的子一个自由度。

【$\mu$相空间】
一个粒子的状态由其动量和位置决定，即由$\mu$-相空间的一个点表示$$(\mathbf{p},\mathbf{r})=(p_x,p_y,p_z;x,y,z)$$$N$-粒子体系的状态由这 $N$个粒子的动量和位置诀定，也即由$\mu -$相空间相应的$N$个点共同示$$(p,r)=(\left\{{\mathbf{p}}_i\right\};\left\{{\mathbf{r}}_i\right\})$$【$\mathrm{\Gamma }$相空间】
$6N$维相空间，相空间中的一个点就代表$N$-粒子体系的一个状态。孤立体系能量守恒，该体系的所有可能的状态构成了$\mathrm{\Gamma }-$相空间中的等能面。

实例

(1) 混沌系统的相空间
如果系统是混沌系统，相轨线在一个有限的区域内不断环绕，而无法看到轨线的闭合与重复。Classic examples of phase diagrams from chaos theory are: (参考数学之旅笔记有关混沌理论的部分)

• the Lorenz attractor;
• population growth (i.e. logistic map);
• parameter plane of complex quadratic polynomials with Mandelbrot set.

(2) 单摆的相空间

• 动画参考Simple Pendulum with Phase Space Flow，和PengTitus视频讲的内容对照。
  
• 第二个交互动画Pendulum - interactive phase portrait—Geogebra

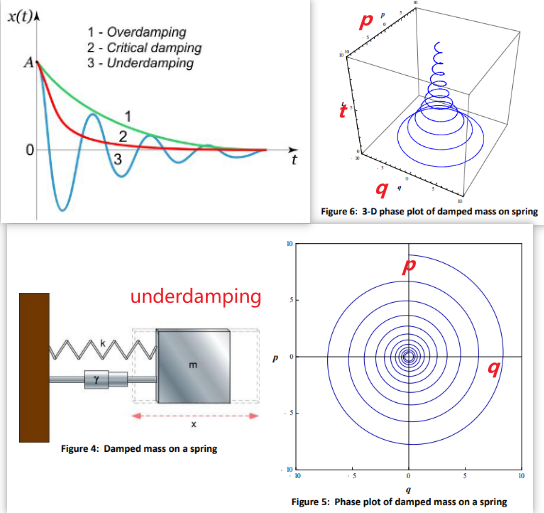
如果是匀速圆周运动的系统，那么相平面就是一个平行于横轴的线段。

如果这个单摆有阻力，且给定初始位置的角速度为零，那么其相平面对应的轨迹根据阻力的大小可能有不同的情况。最下面右边的图，其实就是Phase space of a dynamic system with focal stability, showing one phase space trajectory.

(3) 量子力学的相空间

参考蔡同学的回答以及Phase space-wiki

(4) 热力学和统计力学的相空间
The term phase space has two meanings:

•  A microstate (微观状态) of the system. It is used in the same sense as in classical mechanics. 其实就是上面说的$6N$维相空间；
• A macrostate (宏观状态) of the system, such as pressure, temperature, etc. For instance, one may view the pressure-volume diagram or entropy-temperature diagrams as describing part of this phase space. A point in this phase space is correspondingly called a macrostate. There may easily be more than one microstate with the same macrostate. For example, for a fixed temperature, the system could have many dynamic configurations at the microscopic level. When used in this sense, a phase is a region of phase space where the system in question is in, for example, the liquid phase, or solid phase, etc. 其实就是物理化学中的【相图】。

由于微观状态比宏观状态多得多，因此第一种意义上的相空间通常是比第二种意义上大得多的【流形】(Manifold)。显然，将系统的每一个细节都记录到分子或原子尺度上需要更多的参数，而不是简单地指定系统的温度或压力。

拓展资料：
(1) 什么是相空间？-浅斟低唱
(2) 简明量子力学笔记
(3) 浅谈统计物理学中相空间概念的教学-教育教学论坛
(4) Phase space and intuition for quantum adiabatic invariants-MIT
(5) 相空间-yang元祐
(6) 相平面(状态空间)分析简介 PengTitus-1  PengTitus-2
(7) 相空间和分布函数-上大老姜
(8) Phase – Space Dynamics
(8) 从牛顿到费曼，相空间：一切物理的舞台

 

状态空间的最小体积

经典粒子的状态由位置和动量确定，在动量和位置的相空间里，一个状态体积？相空间体积确定时(三维位置和动量，六维相空间)，包含多少状态？$$\iiint \iiint \frac{d{p}_{x}d{p}_{y}d{p}_{z}dxdydz}{\delta }$$上面是总的状态体积除以最小的状态数体积，即得到状态数，统计力学给出最小体积是$\delta =h^3$，为什么呢？
立方体盒子(三维无线深势阱)里的微观粒子，微观粒子有量子性，于是波函数在边界上为零，类似于满足驻波条件(左图)，于是有$L={\displaystyle \frac{n_x}{2}{\lambda }_x}$即$k_{x}L=n_x\pi$，其中$n_x=1,2,3,\dots \dots$，$k_x={\displaystyle \frac{2\pi }{{\lambda }_x}}$，同理对$y$和$z$也有类似的公式。于是有$$\begin{array}{c}{\lambda }_x=\frac{2L}{n_x},{\lambda }_y=\frac{2L}{n_y},{\lambda }_z=\frac{2L}{n_z}\\ p_x=\frac{\pi n_x\hslash }{L},p_y=\frac{\pi n_y\hslash }{L},p_z=\frac{\pi n_z\hslash }{L}\\ E=\frac{p^2}{2m}=\frac{{\pi }^2{\hslash }^2}{2m{L}^2}(n_x^2+n_y^2+n_z^2)\end{array}$$(1) 能量是量子化的；
(2) $(n_x,n_y,n_z)$量子数表示粒子状态数，其中$n_x,n_y,n_z=1,2,3,\dots \dots$

状态数在量子空间的计数(右图)，单位体积对应一个状态，能量小于$E$的状态区域在哪里？$$n_x^2+n_y^2+n_z^2\le E\frac{2m{L}^2}{{\pi }^2{\hslash }^2}=R^2$$小于能量$E$的状态数目应该是(三维空间，八分之一个球)$$N_E=\frac{1}{8}\cdot \frac{4\pi }{3}{R}^3=\frac{1}{6}(2mE{)}^{3/2}\frac{L^3}{{\pi }^2{\hslash }^3}$$另一方面，在相空间里，各向同性球体(六重空间，整个球体)$$N_E=\iiint \iiint \frac{d{p}_{x}d{p}_{y}d{p}_{z}dxdydz}{\delta }=\frac{4\pi p^3}{3}V/\delta$$根据$E={\displaystyle \frac{p^2}{2m}}$和$V=L^3$，两个式子比较即可得到$\delta =h^3$。

实际上不需要做三维的东西，只需要做简单一维无线深势阱就行$$E=\frac{p^2}{2m}=\frac{{\pi }^2{\hslash }^2}{2m{L}^2}{n}_x^2{n}_x=1,2,3,\dots \dots$$小于能量$E$的状态数目，即能量$E$所对应的$n_x$$$N_E=\frac{L}{\pi \hslash }\sqrt{2mE}=\frac{2}{h}L{p}_{x,max}$$一维相空间
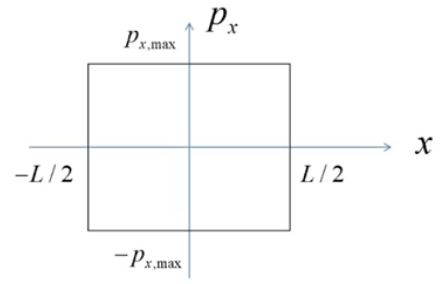$$N_E=\iint \frac{d{p}_{x}dx}{\delta }=\frac{2p_{x,max}L}{\delta }$$于是有相空间最小体积$\delta =h$

一维谐振子
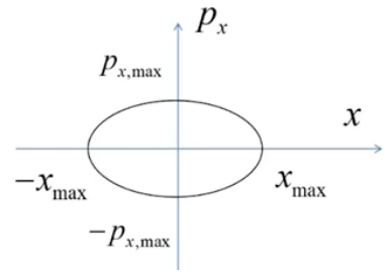$$E=\frac{p^2}{2m}+\frac{1}{2}m{\omega }^2{x}^2$$小于能量$E$的状态区域是一个椭圆，椭圆的面积处于最小状态数就是最小体积$$N_E=\iint \frac{d{p}_{x}dx}{\delta }=\frac{\pi \sqrt{2mE}}{\delta }\sqrt{\frac{2E}{m{\omega }^2}}=\frac{2\pi E}{\omega \delta }$$而$$E=(\frac{1}{2}+n)\hslash \omega n=0,1,2,3,\dots \dots$$小于能量$E$的状态数目$$N_E=\frac{E}{\hslash \omega }+\frac{1}{2}\approx \frac{E}{\hslash \omega },n>>1$$比较之后同样可以得到$\delta =h$

思考：为啥一维最小体积是$h$，三维最小体积就是$h^3$，老师也没余给出严格说明，他只是说一个和德布罗意关系式$\lambda ={\displaystyle \frac{h}{p}}$有关。

参考资料：物理教学中的几个概念-清华大学-安宇

学量子力学或者固体物理的时候，很多概念还是不熟悉，理解比较肤浅，下面专门探讨一下，提升对物理概念的感性认识。重点推荐参考资料为中科大课件。

群速度和相速度

群速度：是指波振幅外形上的变化在空间中所传递的速度。我们只需要盯着振幅最大/最小的点，看其向前传递的速度即可。群速度$v_g\equiv {\displaystyle \frac{\partial \omega }{\partial k}}$常被认为是能量或信息顺着波动传播的速度。

相速度：是指波的相位在空间中传递的速度，换句话说，波的任一频率成分所具有的相位即以此速度传递。我们只需要盯着某一个波峰，看它的传播速度即可，该波峰在向前传播的过程中，振幅大小会发生变化，但是该峰的强度始终比它前后位置的振幅大。$v_{\mathrm{p}}=f\lambda ={\displaystyle \frac{\omega }{k}}$

群速度/相速度视频，给出了更形象的展现。同时也说明了，群速度和相速度可能方向相反，群速度可能大于相速度，相速度也可能大于群速度。注意这里探讨的情形只是从数学意义上出发，而不具有量子力学/粒子波函数上的意义，所以包罗了更多的情况。

(1) 相速与频率无关时(角频率$\omega$正比于波矢$k$)，群速(色散关系函数的导函数为常数，也就是相速，这里也是群速)就等于相速，称为无色散；
(2) 频率越高相速越小时，群速小于相速，称为正常色散；
(3) 频率越高相速越大时，群速大于相速，称为反常色散。

问：光在介质中传播的相速度和群速度？
答：参考这里。

问：$n$个不同的波$y_i(x,t)=A\sin (k_{i}x-{\omega }_{i}t)$叠加传播，会有几个群速度和几个相速度？
答：只有一个群速度，相速度有$n-1$个，而且叠加的波的这些相速度和原始组分各自的相速度之间不同，存在复杂数学关系。参考色散、群速度与相速度-彩虹原理

色散

柯西散射公式：$n=A+{\displaystyle \frac{B}{{\lambda }^2}+{\displaystyle \frac{C}{{\lambda }^4}}}$。经常简化为$n=B+{\displaystyle \frac{C}{{\lambda }^2}}$，常见光学材料比如水、玻璃的折射率和电磁波频率密切相关。其推导见这里。

依据不同的演化方程，在传播的时候，波包的包络线(描绘波包轮廓的曲线)可能会保持不变(没有色散)，或者包络线会改变(有色散)。

下图一个正在传播的非色散的波包。

量子力学中，若粒子不受力(势能处处为常数)且初始时波函数为波包且具有初速度，波包中心就会匀速运动，但同时波包会扩散(越变越宽，越变越矮)，这是因为存在色散。如下图(对应自由粒子的波包．注意图中波包仅画出了振幅，没画出波函数)(参考小时物理)

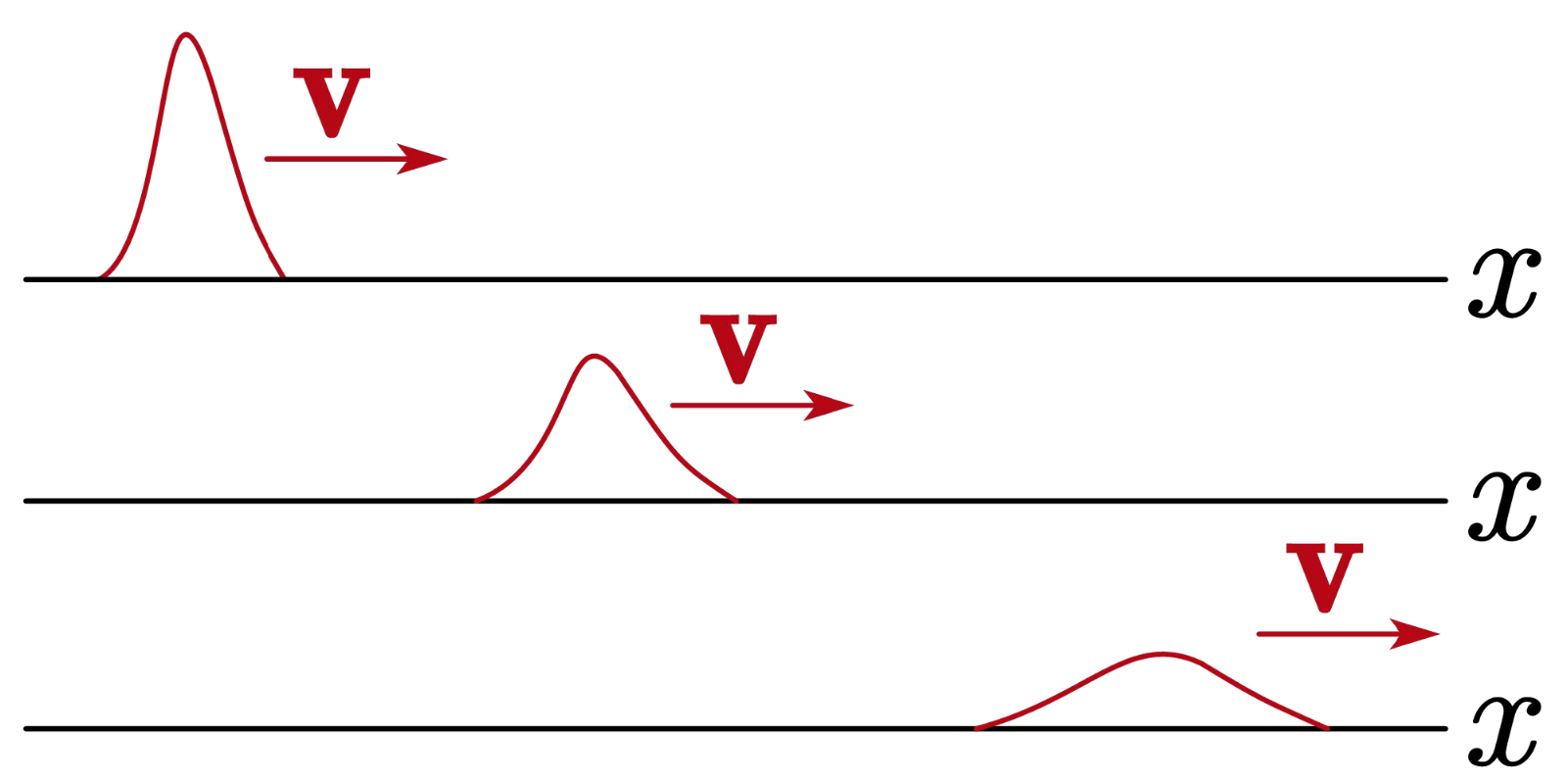
 在一般的量子力学问题中，波包的长度非常小(原子尺度)．当我们回到宏观中，波包的大小就可以忽略不计，测量其位置的不确定性也可以忽略不计，从而把波包近似成一个固定位置的质点，波包的整体速度就是质点的速度，这样就得到了匀速运动的宏观质点．可见量子力学和经典力学是不矛盾的，只是描述的尺度不同。

问：固体物理中色散关系$\omega =\omega (q)$的物理意义是什么？
答：参考这里，
(1) $\omega$对应能量($E=\hslash \omega p=\hslash k$)，色散关系也就是声子能量-波矢(动量)关系，在波矢空间(动量空间)中，状态数与波矢空间的体积成正比，所以$\omega -q$其实反映的不同波矢下的能量密度。比如波矢$q$占据的空间(对应的能量密度/态密度)其实是以其为半径的球体的外薄层，或者说表面积和$dq$的乘积。

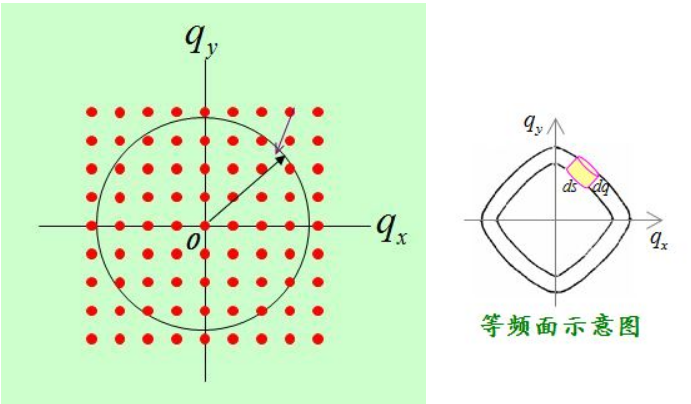
注意位置空间的周期性和动量空间(波矢空间)的对偶性，二者均具有周期性，而且位置空间的周期(上图中的一维晶格周期为$a$)和动量空间的周期(${\displaystyle \frac{2\pi }{a}}$)的乘积为$2\pi$。

(2) 大致可以这样来理解：
体系有很复杂的相互作用，但是可以视为一大堆几乎相互作用比较弱的准粒子的集合，而这些准粒子的动能就是由色散关系给出的。知道了它就可以得到体系的很多性质(当然一些多粒子的关联性质得不到)。

波包

用平面波描述物质波会出现什么问题？

平面波我们写作$$e^{i(kx-\omega t)}=\cos (kx-\omega t)+i\sin (kx-\omega t)$$画图像的时候，我们画实部就可以。$k$是波矢，$\omega$是角频率。那么相速度：(非相对论下的动能公式)$$v_p=\frac{\omega }{k}=\frac{\hslash \omega }{\hslash k}=\frac{E}{p}=\frac{\frac{1}{2}x{v}^2}{mv}=\frac{1}{2}v$$即物质波的相速度等于我们用质点的观念去看问题的时候的质点运动速度的一半，这样就会发生十分荒谬的情况，即物质波不断落后质点。

在量子论时代，人们认识到这个问题后，发现要用波包来描述每个微观质点的物质波，所谓波包就是形状中间有个鼓起的地方，一般是单峰钟形，不见得前后对称。

群速度：波包的外廓绝对值最大的那一点的移动速度，不用关注波包内的振荡情况。

波包的组成：波包是由各种不同波长的平面波的恰当的线性叠加来组成的。

波包只能有一个中央(最大)凸起。$\psi (x)=\cos (2\pi x)+\cos (\pi x)+\cos \left(\frac{2\pi }{3}x\right)$仍然是一个周期函数(这里我们考虑$t=0$)，是这三个参与线性叠加的平面波的波长是这三个波的最小公倍数，比如这里的波长就是6。要形成波包，那么参与线性叠加的平面波的波长的最小公倍数是无穷大，这样才能只有一个中央凸起。其实很容易实现，比如有的平面波波长是有理数，有的是无理数(不能化成分数)，这样肯定就没有最小公倍数。为了讲求波包的形状合理，还是得写成如下形式：$$\psi (x)={\int }_{-\mathrm{\infty }}^{+\mathrm{\infty }}dkA(k)e^{ikx}$$

参考资料：
(1) 量子力學(三)波包
(2) 小时物理
(3) 相速度與群速度、群速度計算、電磁波與粒子的速度、電磁波與物質波

散射截面

 

参考资料：
(1) 如何理解微分散射截面?-知乎
(2)

 

介电常数和折射率

电容率-Wikii

证明折射率和介电常数的关系-小木虫

 

 

参考资料：
(1) 水的折射率与相对介电常数有矛盾吗？-知乎
(2)