天体运行
开普勒发现了椭圆轨道,不过当时并没有人能给出解释,直到牛顿时代才揭开了其中的奥秘。根据牛顿的万有引力定律可以计算出,两个天体组成的系统,它们绕质心运行的轨道只可能有三种情况:椭圆、抛物线、双曲线,其中圆轨道是椭圆轨道的一种特例。
行星轨道为什么是椭圆?可以参考下面的资料:
(1) 科普时报
(2) Planetary orbits and barycenters
(3) 地球不是绕着太阳转?八大行星和太阳,绕着一个看不见的点旋转
(4) Eccentricity—数学乐
圆锥曲线
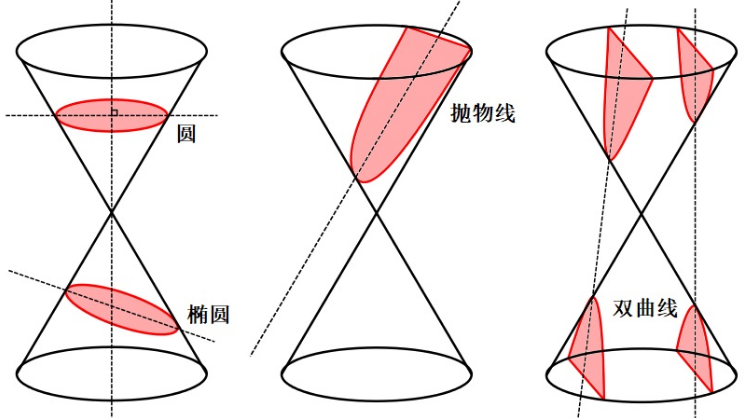
圆锥曲线这个词古希腊的时候就被阿波罗尼斯提出,也有以他名字命名的"阿波罗尼斯圆"。为什么用圆锥曲线给这一类曲线命名?因为可以通过切割圆锥的办法得到。
矩阵表示
在笛卡尔坐标系内,二元二次方程的图像可以表示圆锥曲线,并且所有圆锥曲线都以这种方式引出。方程有如下形式$$ A x^{2}+B x y+C y^{2}+D x+E y+F=0 $$其中参数\(A\)、\(B\)和\(C\)不全为零。可以用如下的矩阵来等价表示$$ \left[\begin{array}{ll} x & y \end{array}\right]\left[\begin{array}{cc} A & B / 2 \\ B / 2 & C \end{array}\right]\left[\begin{array}{l} x \\ y \end{array}\right]+\left[\begin{array}{ll} D & E \end{array}\right]\left[\begin{array}{l} x \\ y \end{array}\right]+F=0 $$或者写成$$ \left[\begin{array}{lll} x & y & 1 \end{array}\right]\left[\begin{array}{ccc} A & B / 2 & D / 2 \\ B / 2 & C & E / 2 \\ D / 2 & E / 2 & F \end{array}\right]\left[\begin{array}{l} x \\ y \\ 1 \end{array}\right]=0 $$
椭圆:
参考资料:
(1) 圆锥曲线的极坐标方程—小时百科
(2) 圆锥曲线—李永乐
(3) 圆锥曲线的启示—张天蓉
(4) 圆锥曲线—PengTitus