线性代数-1

参考资料：

宏观思考：

  • 矩阵是一组映射关系。通过对线性映射关系进行抽象，将与之无关的信息剔除，而得到的独立概念，这和计算机编程中的抽象极其相似，通过进一步研究，得出了很多矩阵的性质、法则。
  • 线性代数的本质是解决有限维向量空间以及线性映射的问题，对于一个一般的线性映射，如何将其分解为好的线性映射，对于一个好的线性映射，如何去刻画其矩阵。好的线性映射，就是其矩阵表示起来尽可能简单，比如说有很多位置上的元素都是零，类似对角矩阵、上三角矩阵、若尔当型。
  • 算子是一种特殊的线性映射，其对应的矩阵是方阵(复数域上是埃尔米特矩阵)，算子的矩阵表示(核心为谱定理)。
  • 深刻理解几何意义，熟练掌握代数方法。(谢启鸿)

【向量点乘】

(1) \(\left[\begin{array}{l} 4 \quad 2 \end{array}\right] \cdot\left[\begin{array}{c} -1 \\ 2 \end{array}\right]=-4+4=0\)表示的是向量\((4,2)\)和\((-1,2)\)相互垂直。

(2) 可以从相像跷跷板(see-saw ['si:sɔ:] )，一边长度是\(1\)，一边长度是\(2\)，两者的各自的权重分别是\(4\)和\(2\)，那么这个跷跷板最终会实现平衡，\(w_{1} v_{1}+w_{2} v_{2}=0\)。

(3) 向量\( \boldsymbol{p}=\left(p_{1}, p_{2}, p_{3}\right) \)表示的是商品的价格，向量\(\boldsymbol{q}=\left(q_{1}, q_{2}, q_{3}\right)\)表示的是买和卖的价格，买用正号表示，卖用负号表示，那么总的净收入$$\text { Income }=\left(q_{1}, q_{2}, q_{3}\right) \cdot\left(p_{1}, p_{2}, p_{3}\right)=q_{1} p_{1}+q_{2} p_{2}+q_{3} p_{3}$$(4) 几何意义如下图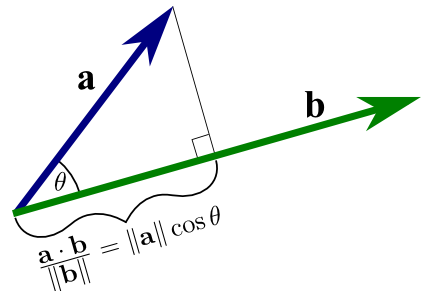【向量模长】
对于四维向量，模长计算方式为\(\sqrt{v_{1}^{2}+v_{2}^{2}+v_{3}^{2}+v_{4}^{2}}\)。

【基向量】

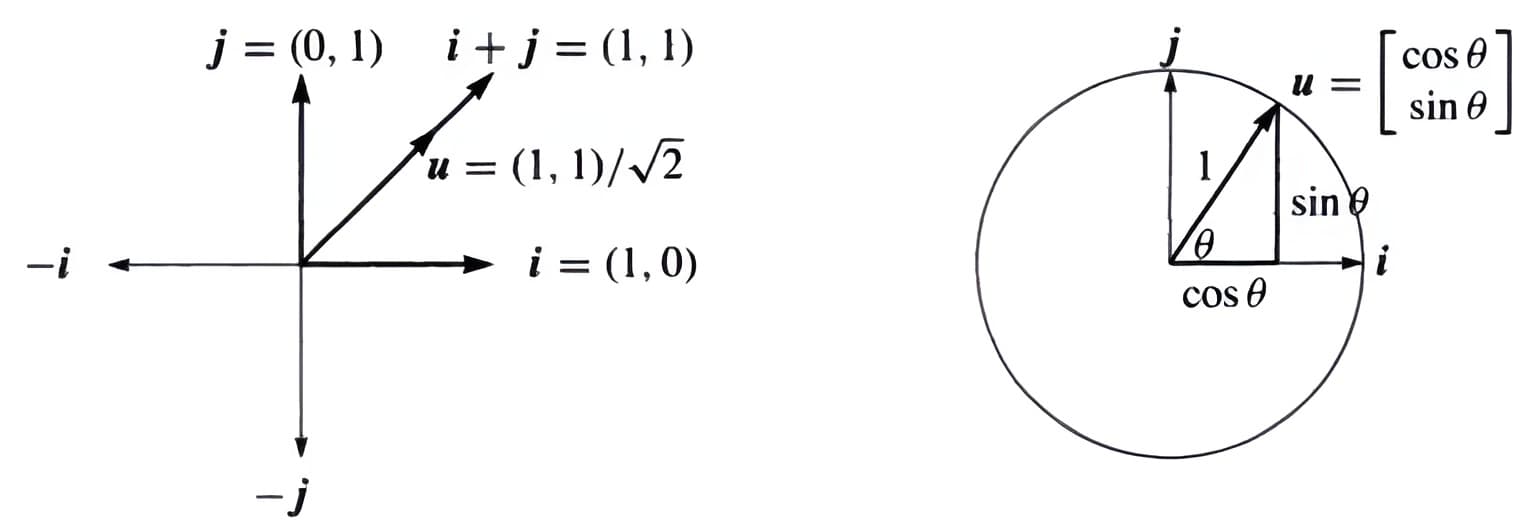
向量角度理解——\(\cos \theta=\boldsymbol{v} \cdot \boldsymbol{w} /\|\boldsymbol{v}\|\|\boldsymbol{w}\|\)

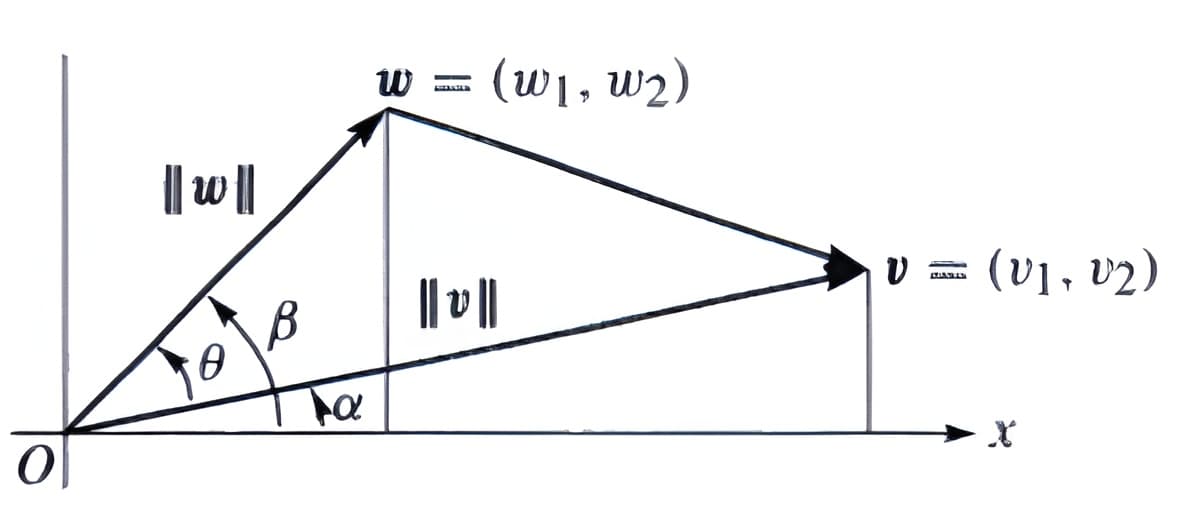
我们知道\(\cos \alpha=v_{1} /\|\boldsymbol{v}\|\)，而\(\sin \alpha=v_{2} /\|\boldsymbol{v}\|\)，很容易知道\(\cos \beta \cos \alpha+\sin \beta \sin \alpha\)，积化和差得到\(\cos (\beta-\alpha)\)，也就是\(\cos \theta\)。

向量角度理解——\(2 a b \leq a^{2}+b^{2}\)
对于任意两个二维向量有\(\displaystyle\frac{\boldsymbol{v} \cdot \boldsymbol{w}}{\|\boldsymbol{v}\|\|\boldsymbol{w}\|}=\cos \theta\)，于是\(|\boldsymbol{v} \cdot \boldsymbol{w}| \leq\|\boldsymbol{v}\|\|\boldsymbol{w}\|\)。如果\(\boldsymbol{v}=(a, b)\)，\(\boldsymbol{w}=(b, a)\)，显然就可以推出\(2 a b \leq a^{2}+b^{2}\)

 

矩阵简介和\(LU\)分解

解线性方程

对于方程组  \(\begin{aligned} x-2 y &=1 \\ 3 x+2 y &=11 \end{aligned}\)，我们从如下来思考

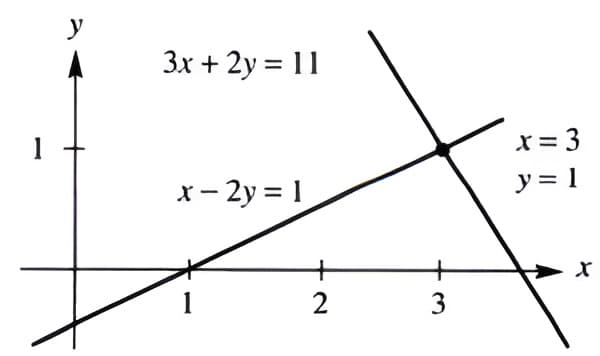
\(x\left[\begin{array}{l} {1} \\ {3} \end{array}\right]+y\left[\begin{array}{r} {-2} \\ {2} \end{array}\right]=\left[\begin{array}{r} {1} \\ {11} \end{array}\right]=\boldsymbol{b}\)            \(3(\text { column } 1)+1(\text { column } 2)=\boldsymbol{b}\)

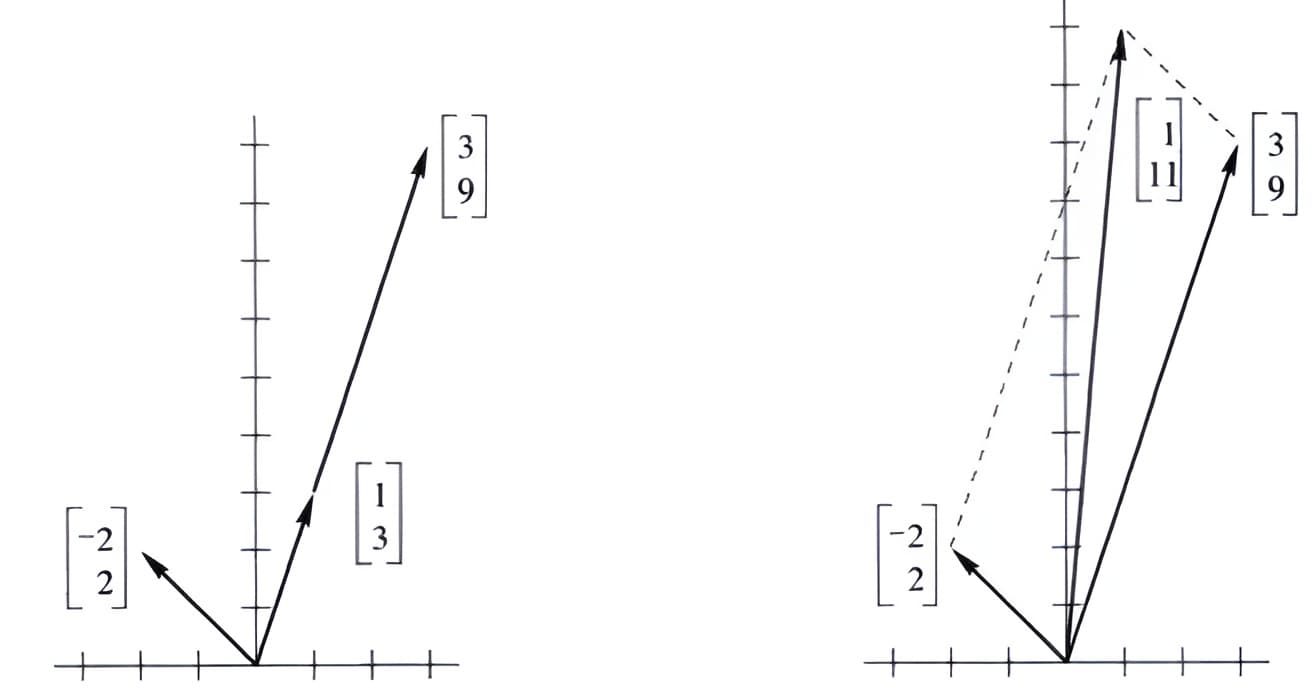
矩阵方程\(\left[\begin{array}{rr} {1} & {-2} \\ {3} & {2} \end{array}\right]\left[\begin{array}{l} {x} \\ {y} \end{array}\right]=\left[\begin{array}{r} {1} \\ {11} \end{array}\right]\)，其中系数矩阵为\(A=\left[\begin{array}{rr} {1} & {-2} \\ {3} & {2} \end{array}\right]\)，一般的矩阵方程\(A \boldsymbol{x}=\boldsymbol{b}\)

线性代数角度理解三元一次方程

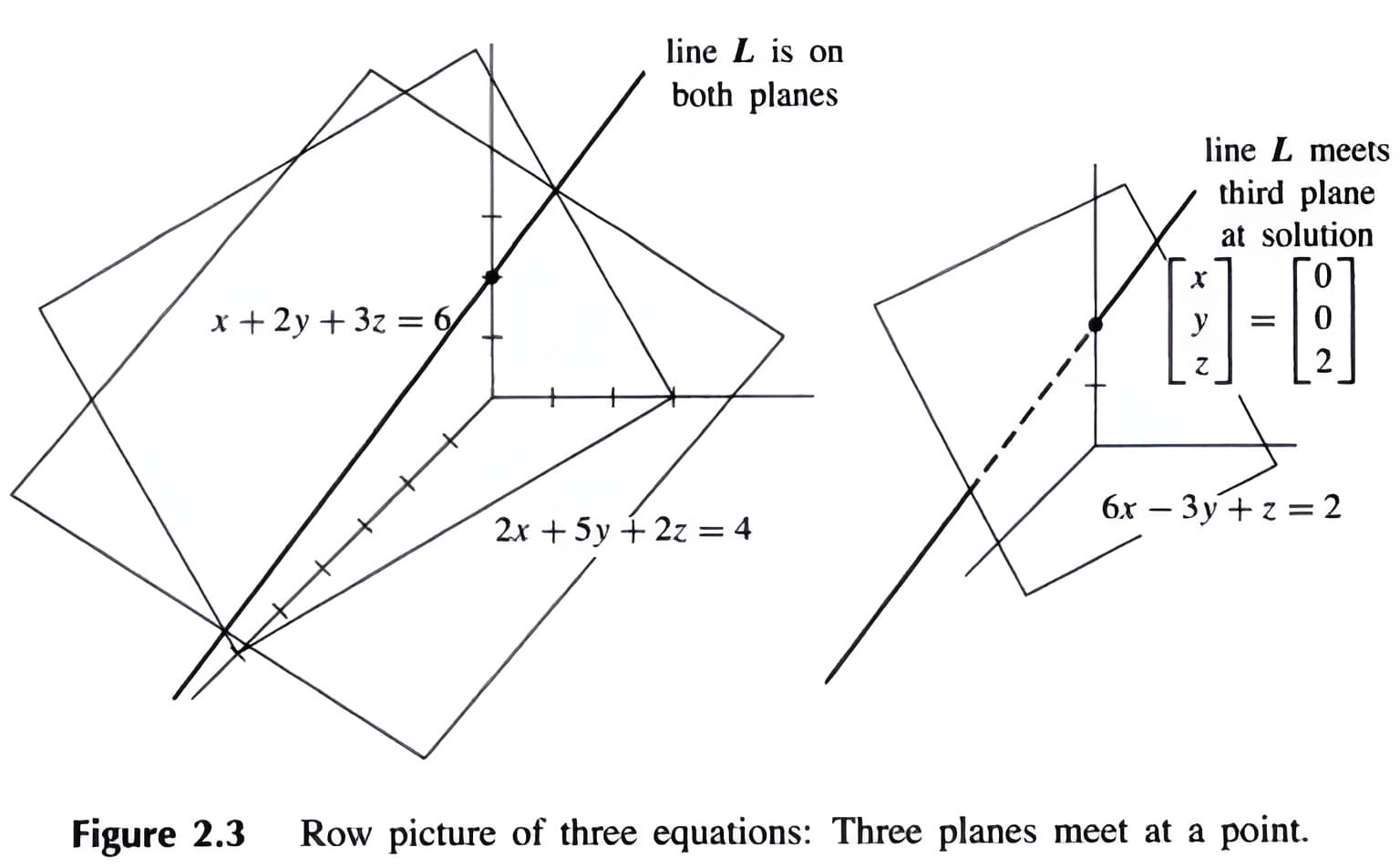
\(\begin{aligned} x+2 y+3 z &=6 \\ 2 x+5 y+2 z &=4 \\ 6 x-3 y+z &=2 \end{aligned}\) 为例

(1) 从row picture的维度看，表示的是三个平面相交的地方(可能是点、线，可能没有相交)
(2) 从column picture的维度看，表示的是三个列向量的线性组合得到一个新的列向量(当然，方程无解的话，表示这种线性组合是不存在的)。
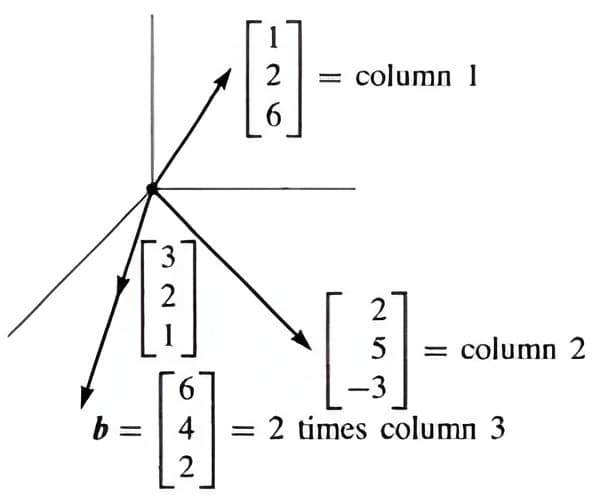\(x\left[\begin{array}{l} {1} \\ {2} \\ {6} \end{array}\right]+y\left[\begin{array}{r} {2} \\ {5} \\ {-3} \end{array}\right]+z\left[\begin{array}{l} {3} \\ {2} \\ {1} \end{array}\right]=\left[\begin{array}{l} {6} \\ {4} \\ {2} \end{array}\right]\)矩阵方程\(\left[\begin{array}{rrr} {1} & {2} & {3} \\ {2} & {5} & {2} \\ {6} & {-3} & {1} \end{array}\right]\left[\begin{array}{l} {x} \\ {y} \\ {z} \end{array}\right]=\left[\begin{array}{r} {6} \\ {4} \\ {2} \end{array}\right]\)

Matlab表示上述三元线性方程
\(A=\left[\begin{array}{lllllllll} {1} & {2} & {3} ;& {2} & {5} & {2}; & {6} & {-3} & {1} \end{array}\right]\)
\(\boldsymbol{x}=[0 ; 0 ; 2]\)
for J=1: 3;
for I=1: 3;
b(I)=b(I)+A(I, J) * x(J);

\(\text {Row at a time } \boldsymbol{b}=[A(1, i) * \boldsymbol{x} ; A(2, i) * \boldsymbol{x} ; A(3, i) * \boldsymbol{x}]\)
\(\text { Column at a time } \boldsymbol{b}=A(:, 1) * \boldsymbol{x}(1)+A(:, 2) * \boldsymbol{x}(2)+A(:, 3) *\boldsymbol{x}(3)\)

三元一次方程组的变换
对于方程组\(\begin{array}{c} {x+3 y+5 z=4} \\ {x+2 y-3 z=5} \\ {2 x+5 y+2 z=8} \end{array}\)，我们可以写成\(\left[\begin{array}{rrr} {1} & {3} & {5} \\ {1} & {2} & {-3} \\ {2} & {5} & {2} \end{array}\right]\left[\begin{array}{l} {x} \\ {y} \\ {z} \end{array}\right]=\left[\begin{array}{r} {4} \\ {5} \\ {8} \end{array}\right]= \boldsymbol{b}\)
第一个方程乘以1+第二个方程乘以1+第三个方程乘以(-1)，我们会发现等式两边不相等。这种运算方式等价于得到下面矛盾的情况(说明解不存在)$$0=\left[\begin{array}{lll} {1} & {1} & {-1} \end{array}\right]\left[\begin{array}{c} {x+3 y+5 z} \\ {x+2 y-3 z} \\ {2 x+5 y+2 z} \end{array}\right]=\left[\begin{array}{cc} {1} & {1-1} \end{array}\right]\left[\begin{array}{c} {4} \\ {5} \\ {8} \end{array}\right]=-1$$

【高斯消元法】(Gauss–Jordan elimination)
(1) 有唯一解的情况
举个简单的例子，消元之前为\(\begin{array}{c} {x-2 y=1} \\ {3 x+2 y=11} \end{array}\)，消元之后得到的是\(\begin{array}{r} {x-2 y=1} \\ {8 y=8} \end{array}\)

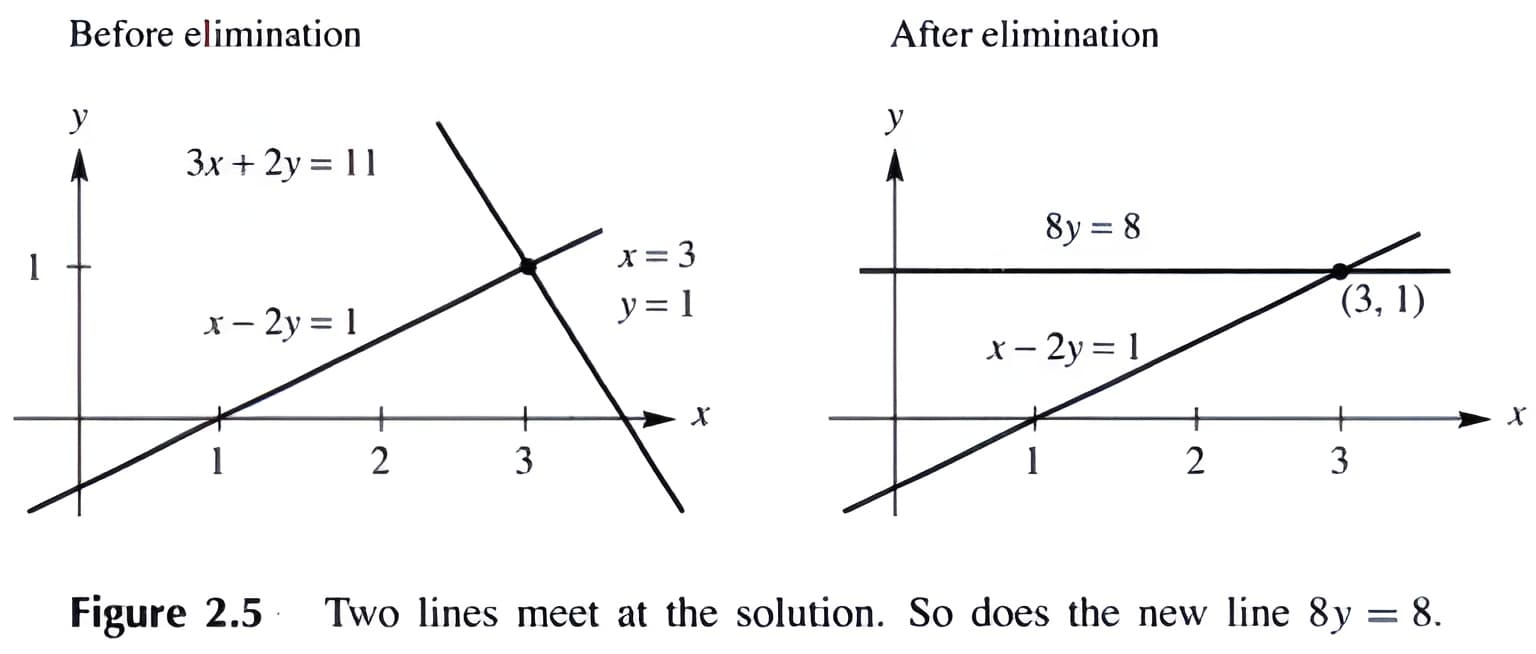
(2) 没有解的情况：\(\begin{array}{rlrl}x-2 y & =1 & x-2 y & =1 \\ 3 x-6 y & =11 & 0 y & =8\end{array}\)

(3) 无穷多解的情况：\(\begin{array}{rrr}x-2 y=1 & x-2 y=1 \\ 3 x-6 y=3 & 0 y=0\end{array}\)

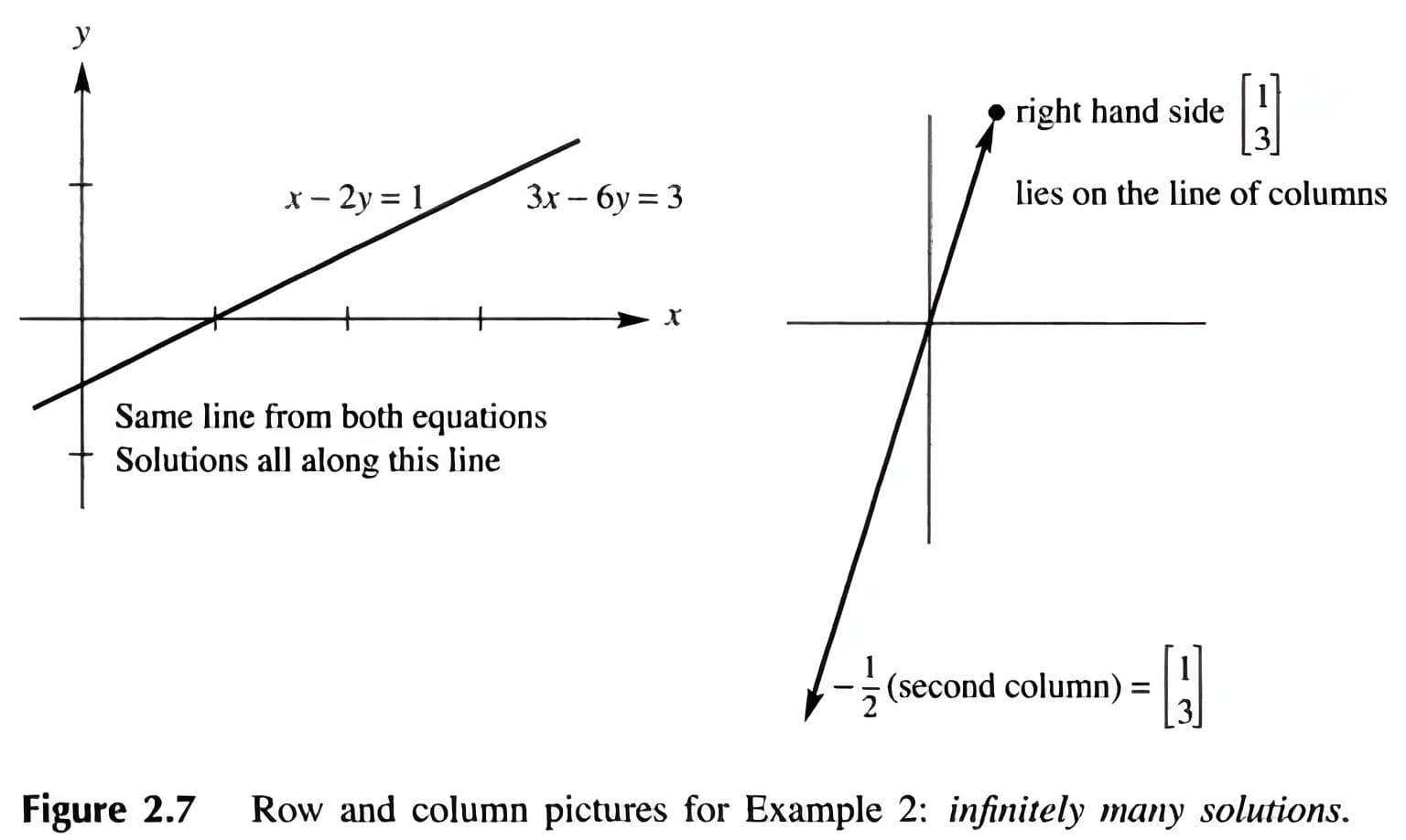
高斯消元法的核心是要得到上三角，然后从下到上back substutition(可能遇到需要换行的情况)

【初等矩阵】(elementary matrix)：由单位矩阵经过一次初等变换得到的矩阵消元矩阵

【消元矩阵】(elimination matrix)：\(E=\left[\begin{array}{rrr} {1} & {0} & {0} \\ {-2} & {1} & {0} \\ {0} & {0} & {1} \end{array}\right]\)表示的是第二行减去第一行的两倍

【置换矩阵】(permutation matrix)：\(P_{23}=\left[\begin{array}{lll} {1} & {0} & {0} \\ {0} & {0} & {1} \\ {0} & {1} & {0} \end{array}\right]\)表示第二行和第三行互换。
(1) 对于\(n\)阶置换矩阵，总的可能性有\(n ! \)种可能；
(2) \(P^{-1}=P^\mathrm{T}\)，即\(P^\mathrm{T} P=I \)；对于这一点我们可以从两个方面理解，首先对\(P\)置换之后，和\(P\)相乘，那么正好左边第\( i\)行乘以右边第\( i\)列得到\(1\)(正好在某个对应的位置上元素都是\(1\)，其他都是\(0\))；另一个方面理解，置换就相当于复原原来的行变换。

【矩阵的转置】(Transpose of Matrix)：转置相当于沿着对角线进行翻转。
(1) 若\(A \)是对称阵，那么\( A^\mathrm{T}=A\)
(2) 矩阵乘积的转置\((A B)^\mathrm{T}=B^\mathrm{T}A^\mathrm{T} \)
(3) 给定的一个矩阵\( R\)，\( R\)可以不是方阵，则乘积\( R^\mathrm{T}R\)一定是对称阵，$$\left(R^{\mathrm{T}}R\right)^{\mathrm{T}}=R^{\mathrm{T}}\left(R^{\mathrm{T}}\right)^{\mathrm{T}}=R^{\mathrm{T}}R$$

【增广矩阵】(augmented matrix)：就是在系数矩阵的右边添上一列，这一列是线性方程组的等号右边的值。

【Vector-Vector Products】$$ x^T y \in \mathbb{R}=\left[\begin{array}{llll} x_1 & x_2 & \cdots & x_n \end{array}\right]\left[\begin{array}{c} y_1 \\ y_2 \\ \vdots \\ y_n \end{array}\right]=\sum_{i=1}^n x_i y_i $$上面的乘法叫作内积/点乘。

外积如下$$ x y^T \in \mathbb{R}^{m \times n}=\left[\begin{array}{c} x_1 \\ x_2 \\ \vdots \\ x_m \end{array}\right]\left[\begin{array}{llll} y_1 & y_2 & \cdots & y_n \end{array}\right]=\left[\begin{array}{cccc} x_1 y_1 & x_1 y_2 & \cdots & x_1 y_n \\ x_2 y_1 & x_2 y_2 & \cdots & x_2 y_n \\ \vdots & \vdots & \ddots & \vdots \\ x_m y_1 & x_m y_2 & \cdots & x_m y_n \end{array}\right] $$利用外积，我们可以将矩阵\(A\)进行如下表示$$ A=\left[\begin{array}{lllll} \mid & \mid & & \mid \\ x & x & \cdots & x \\ \mid & \mid & & \mid \end{array}\right]=\left[\begin{array}{cccc} x_1 & x_1 & \cdots & x_1 \\ x_2 & x_2 & \cdots & x_2 \\ \vdots & \vdots & \ddots & \vdots \\ x_m & x_m & \cdots & x_m \end{array}\right]=\left[\begin{array}{c} x_1 \\ x_2 \\ \vdots \\ x_m \end{array}\right]\left[\begin{array}{llll} 1 & 1 & \cdots & 1 \end{array}\right]=x \mathbf{1}^T $$

【Matrix-Vector Products】
将矩阵\(A\)写成行向量的形式，于是\(Ax\)可以表示为$$ y=A x=\left[\begin{array}{ccc} - & a_1^T & - \\ - & a_2^T & - \\ & \vdots & \\ - & a_m^T & - \end{array}\right] x=\left[\begin{array}{c} a_1^T x \\ a_2^T x \\ \vdots \\ a_m^T x \end{array}\right] $$矩阵\( A\)左乘一个行向量\(x^T\)$$ y^T=x^T A=x^T\left[\begin{array}{cccc} \mid & \mid & & \mid \\ a_1 & a_2 & \cdots & a_n \\ \mid & \mid & & \mid \end{array}\right]=\left[\begin{array}{llll} x^T a_1 & x^T a_2 & \cdots & x^T a_n \end{array}\right] $$或者表示为$$ \begin{aligned} y^T &=x^T A \\ &=\left[\begin{array}{llll} x_1 & x_2 & \cdots & x_n \end{array}\right]\left[\begin{array}{ccc} - & a_1^T & - \\ - & a_2^T & - \\ \vdots \\ - & a_m^T & - \end{array}\right] \\ &=x_1\left[\begin{array}{lll} -a_1^T & - \end{array}\right]+x_2\left[\begin{array}{ll} -a_2^T \end{array}\right]+\ldots+x_n\left[\begin{array}{lll} -a_n^T & - \end{array}\right] \end{aligned} $$

【Matrix-Matrix Products】$$A B=\left[\begin{array}{ll} {3} & {4} \\ {1} & {5} \\ {2} & {0} \end{array}\right]\left[\begin{array}{ll} {2} & {4} \\ {1} & {1} \end{array}\right]=(3 \text { by } 2)(2 \text { by } 2)$$第一种是我们传统的做法，左边的每一行和右边的每一列点乘，第二种做法是左边的每一列和右边的每一行相乘$$A B=\left[\begin{array}{l} {3} \\ {1} \\ {2} \end{array}\right]{\left[\begin{array}{ll} {2} & {4} \end{array}\right]}+\left[\begin{array}{l} {4} \\ {5} \\ {0} \end{array}\right]{\left[\begin{array}{ll} {1} & {1} \end{array}\right]}=\left[\begin{array}{rr} {6} & {12} \\ {2} & {4} \\ {4} & {8} \end{array}\right]+\left[\begin{array}{ll} {4} & {4} \\ {5} & {5} \\ {0} & {0} \end{array}\right]=\left[\begin{array}{rr} {10} & {16} \\ {7} & {9} \\ {4} & {8} \end{array}\right]$$【分块矩阵】(block matrix )：我们通常的计算是，用\(A\)的每一行去和\(B\)的每一列做内积(每个对应元素乘积加和得到新的元素)；但是这里，我们把矩阵A看作是由多个列向量组成的，而矩阵B是由多个行向量组成的，两次分块矩阵乘法运算(outer products)之后分别得到两个新的矩阵(而不是一个数)。$$\begin{aligned} \left[\begin{array}{ll} {1} & {4} \\ {1} & {5} \end{array}\right]\left[\begin{array}{ll} {3} & {2} \\ {1} & {0} \end{array}\right] &=\left[\begin{array}{l} {1} \\ {1} \end{array}\right]\left[\begin{array}{ll} {3} & {2} \end{array}\right]+\left[\begin{array}{l} {4} \\ {5} \end{array}\right]\left[\begin{array}{ll} {1} & {0} \end{array}\right] =\left[\begin{array}{ll} {3} & {2} \\ {3} & {2} \end{array}\right]+\left[\begin{array}{ll} {4} & {0} \\ {5} & {0} \end{array}\right] \end{aligned}$$学术说法：在数学的矩阵理论中，一个分块矩阵或是分段矩阵就是将矩阵分割出较小的矩形矩阵，这些较小的矩阵就称为区块。换个方式来说，就是以较小的矩阵组合成一个矩阵。分块矩阵的分割原则是以水平线和垂直线进行划分。分块矩阵中，位在同一行(列)的每一个子矩阵，都拥有相同的列数(行数)。再举一个例子如下：$$ \begin{aligned} &P=\left[\begin{array}{llll} 1 & 1 & 2 & 2 \\ 1 & 1 & 2 & 2 \\ 3 & 3 & 4 & 4 \\ 3 & 3 & 4 & 4 \end{array}\right]=\left[\begin{array}{ll} P_{11} & P_{12} \\ P_{21} & P_{22} \end{array}\right] \\ &P_{11}=\left[\begin{array}{ll} 1 & 1 \\ 1 & 1 \end{array}\right], P_{12}=\left[\begin{array}{ll} 2 & 2 \\ 2 & 2 \end{array}\right], P_{21}=\left[\begin{array}{ll} 3 & 3 \\ 3 & 3 \end{array}\right], P_{22}=\left[\begin{array}{ll} 4 & 4 \\ 4 & 4 \end{array}\right] \end{aligned} $$

通过将大的矩阵通过分块的方式划分，并将每个分块看做另一个矩阵的元素，这样之后再参与运算，通常可以让计算变得清晰甚至得以大幅简化。例如，有的大矩阵可以通过分块变为对角矩阵或者是三角矩阵等特殊形式的矩阵。

【帕斯卡矩阵】(Pascal Matrix)：由杨辉三角形表组成的矩阵称为帕斯卡矩阵。 杨辉三角形表是二次项\((x+y)^n\) 展开后的系数随自然数\(n\)的增大组成的一个三角形表。 pascal是矩阵实验室(Matrix Laboratory)MATLAB中的函数，利用pascal函数可以在矩阵实验室中方便的得到任意阶帕斯卡矩阵。

Image result for 杨辉三角

帕斯卡矩阵

矩阵的特点：$$\left[\begin{array}{ccc} {1} & {1} & {} \\ {1} & {1} & {1} \\ {1} & {2} & {1} & {1} \\ {1} & {3} & {3} & {1} \end{array}\right]\left[\begin{array}{l} {1} \\ {1} \\ {1} \\ {1} \end{array}\right]=\left[\begin{array}{c} {1} \\ {2} \\ {4} \\ {8} \end{array}\right] \quad\left[\begin{array}{ccc} {1} & {1} & {1} \\ {1} & {1} & {x} \\ {1} & {2} & {1} & {x^{2}} \\ {1} & {3} & {3} & {1} \end{array}\right]\left[\begin{array}{c} {1} \\ {x} \\ {x^{2}} \\ {x^{3}} \end{array}\right]=\left[\begin{array}{c} {1} \\ {1+x} \\ {(1+x)^{2}} \\ {(1+x)^{3}} \end{array}\right]$$

参考资料：
(1) 杨辉三角—数学乐

【有向图(direct graph)】有向图在数学上是表示物件与物件之间的关系的方法，是图论的基本研究对象。 一个图看起来是由一些小圆点(称为顶点或结点)和连结这些圆点的直线或曲线(称为边)组成的。 如果给图的每条边规定一个方向，那么得到的图称为有向图，其边也称为有向边。
上面两个图分别对应于矩阵\(\left[\begin{array}{ll} {1} & {1} \\ {1} & {0} \end{array}\right]\)和矩阵\(\left[\begin{array}{lll} {1} & {1} & {1} \\ {1} & {0} & {0} \\ {1} & {0} & {0} \end{array}\right]\)。
第一个图形走两步对应矩阵\(\left[\begin{array}{ll} {1} & {1} \\ {1} & {0} \end{array}\right]^{2}=\left[\begin{array}{ll} {2} & {1} \\ {1} & {1} \end{array}\right]\)
注：除了有向图，还有无向图，都可以用【邻接矩阵】(adjacency matrix)来表示。


【逆矩阵】(inverse matrix)

  • 一个矩阵有逆矩阵的充要条件(下列几个条件等价)：
    • 矩阵的行列式不为\(0\)；
    • 是满秩矩阵(\(n\) pivots)；
    • 合同标准型是单位矩阵;
  • 一个矩阵不可能同时有两个不同的逆矩阵；
  • 如果\( A\mathbf{x}=\mathbf{0}\)，那么只有当\( \mathbf{x}=\mathbf{0}\)为唯一解的情况下\(A\)才可能有逆矩阵。
  • 二维矩阵的逆矩阵$$\left[\begin{array}{ll} {a} & {b} \\ {c} & {d} \end{array}\right]^{-1}=\frac{1}{a d-b c}\left[\begin{array}{rr} {d} & {-b} \\ {-c} & {a} \end{array}\right]$$
  • \((A B)^{-1}=B^{-1} A^{-1}\)
  • 消元矩阵的逆矩阵$$E=\left[\begin{array}{rrr} {1} & {0} & {0} \\ {-5} & {1} & {0} \\ {0} & {0} & {1} \end{array}\right] \text { and } E^{-1}=\left[\begin{array}{lll} {1} & {0} & {0} \\ {5} & {1} & {0} \\ {0} & {0} & {1} \end{array}\right]$$
  • 求解逆矩阵的方法
    • 最笨的办法：
      对于一个三维矩阵，我们利用\( A x_{1}=e_{1}=(1,0,0)\)，\( A x_{2}=e_{2}=(0,1,0)\)和\( A x_{3}=e_{3}=(0,0,1)\)计算出所有的所有的\(x_{i} \)，然后\( \left[\begin{array}{lll} {x_{1}} & {x_{2}} & {x_{3}} \end{array}\right]\)就是逆矩阵。
    • 实际采用的方法：$$\left[\begin{array}{llll} {A} & {e_{1}} & {e_{2}} & {e_{3}} \end{array}\right]=\left[\begin{array}{rrrrrr} {2} & {-1} & {0} & {1} & {0} & {0} \\ {-1} & {2} & {-1} & {0} & {1} & {0} \\ {0} & {-1} & {2} & {0} & {0} & {1} \end{array}\right] \text { Start Gauss-Jordan }$$首先将左侧的变换成上三角，右侧就变成了下三角，然后左侧的上三角从下到上代回去，将其变成对角矩阵，此时右侧的下三角矩阵就变成了逆矩阵。
  • \(E_{21}\)和\(E_{21}^{-1} \)互为逆矩阵，这里的角标\(21\)表示，采用\(E_{21}\)操作之后，我们要让第二行第一列的元素为\(0\)。例如，如果\(E_{21}\)是第二行减去第一行的\(2\)倍，那么逆矩阵\(E_{21}^{-1} \)表示的是第二行加上第一行的二倍。所以根据这个特点，我们已知\(E_{21}\)，会很容易求得\(E_{21}^{-1} \)。

 

\(LU\)分解

LU分解(lower–upper decomposition)——首先我们举一个\(2\)阶矩阵的例子，对于矩阵\(A=\left[\begin{array}{ll} {2} & {1} \\ {6} & {8} \end{array}\right] \)，不用换行我们就可以实现消元得到上三角矩阵$$E_{21} A=\left[\begin{array}{rr} {1} & {0} \\ {-3} & {1} \end{array}\right]\left[\begin{array}{ll} {2} & {1} \\ {6} & {8} \end{array}\right]=\left[\begin{array}{ll} {2} & {1} \\ {0} & {5} \end{array}\right]=U$$$$E_{ 21 }^{ -1 }E_{ 21 }A=E_{ 21 }^{ -1 }U\Rightarrow \quad A=E_{ 21 }^{ -1 }U=LU=\left[ \begin{array}{ll} { 1 } & { 0 } \\ { 3 } & { 1 } \end{array} \right] \left[ \begin{array}{ll} { 2 } & { 1 } \\ { 0 } & { 5 } \end{array} \right] =\left[ \begin{array}{ll} { 2 } & { 1 } \\ { 6 } & { 8 } \end{array} \right] $$对于三阶矩阵，我们如果同样不用换行就实现消元\(\left(E_{32} E_{31} E_{21}\right) A=U\)，那么\(A=\left(E_{21}^{-1} E_{31}^{-1} E_{32}^{-1}\right) U=LU\)。对于$$A=\left[\begin{array}{lll} {2} & {1} & {0} \\ {1} & {2} & {1} \\ {0} & {1} & {2} \end{array}\right]=\left[\begin{array}{lll} {1} & {0} & {0} \\ {\displaystyle\frac{1}{2}} & {1} & {0} \\ {0} & {\displaystyle\frac{2}{3}} & {1} \end{array}\right]\left[\begin{array}{lll} {2} & {1} & {0} \\ {0} & {\displaystyle\frac{3}{2}} & {1} \\ {0} & {0} & {\displaystyle\frac{4}{3}} \end{array}\right]=L U$$我们可以知道，矩阵\(L\)中的\(1/2\)是对应于原来的消元法中，第二行减去第一行的\(1/2\)(消元矩阵中是\( -1/2\))；\(2/3\)是对应于原来的消元法中，第三行减去第一行的\(2/3\)(消元矩阵中是\(-2/3\))。归根结底，这种方法处理得到的\( U\)中包含的信息与\( A\)一样。总而言之：

  • \( A=LU\)；
  • \(L\)为消元矩阵，下三角；
  • \(U\)为\(A\)的行阶梯型，上三角。

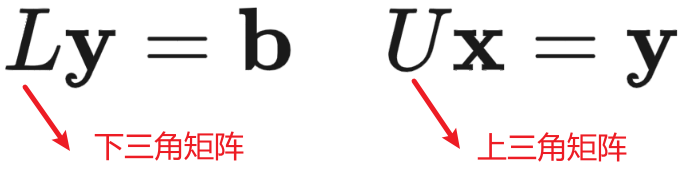分解为 \(L\)和\(U \)之后，原来的\(A \mathbf{x}=\mathbf{b}\)变成先解\(L \mathbf{y}=\mathbf{b}\) 再解 \(U \mathbf{x}=\mathbf{y}\)会变得简单许多。计算变简单的原因是\(L\)是一个下三角(对角元是\(1\))，等于说第一个未知数\( y_{1}\)已经求出来了，然后从上往下带入，即可求得列向量\(\mathbf{y} \)。同理，\(U \)是一个上三角，我们很容易从下往上带入结果，求得\(\mathbf{x}\)。

实际问题中，我们需要求解一系列具有相同系数的线性方程组$$A \mathbf{x}=\mathbf{b}_{1}, A \mathbf{x}=\mathbf{b}_{2}, \cdots, A \mathbf{x}=\mathbf{b}_{p}$$我们可以求出\( A\)的逆，然后分别乘以右侧的列向量；实践中，我们采用如下方法
(1) 用消元法解第一个方程组，同时得到\(A\)的\(L U\)分解；
(2) 用\(L U\)分解解剩下的方程组。

分解之前的换行：前面的\(LU\)分解针对的是不需要换行的\(A\)，如果要换行这个时候我们需要利用置换矩阵，通过对\(A\)适当地行置换(左乘以置换矩阵\(P\))，得到\(PA\)，然后整体对\(PA\)进行\(LU\)分解，即\(PA=LU\)

计算量：设\( A\)为\(n \)阶矩阵，那么高斯消元法的计算量约为\( \displaystyle\frac { 2n^{3} }{  3} \)。包含消元，回代的过程。

存在性和唯一性
(1) 存在性
可逆矩阵\( A\)的顺序主子阵\(A_{k}(k=1, \cdots, n) \)均为可逆矩阵，那么\(A\)有\(LU\)分解。
(2) 唯一性
设 \(n\) 阶可逆阵 \(A\) 有 \(A=L U\), 其中 \(L\) 为下三角矩阵，\(U\) 为上 三角矩阵，且 \(l_{i i}=1, u_{i i} \neq 0(1 \leq i \leq n)\)，则分解唯一。

Pages: 1 2

Leave a Reply