北京大学-吴飙
谈谈量子不可克隆原理-姬扬-科学网
.png)
1900年以前，经典物理学主要有四个问题不能解决(所以才引入量子论)：氢原子光谱的规律、光电效应、黑体辐射、原子的稳定性问题。
麦克斯韦提出了麦克斯韦方程组，但是电磁波是不是超巨相互作用，是不是电磁波有争议。随着阿尔伯特·迈克耳孙在1881年进行的实验和1887年的迈克耳孙-莫雷实验推翻了光以太的存在，赫兹改写了麦克斯韦方程组，将新的发现纳入其中。通过实验，他证明电信号如同麦克斯韦和法拉第预言的那样可以穿越空气(证明了电磁波的存在)，这一理论是发明无线电的基础。他注意到带电物体当被紫外光照射时会很快失去它的电荷，发现了光电效应（后来由阿尔伯特·爱因斯坦给予解释）。麦克斯韦初始提出的方程很复杂，后面赫兹和亥维赛进行了整理修改，得到了我们现在的形式。
瑞利：卡文迪许实验室第二任主任(他的继任者是发现电子的汤姆森)，第一任是麦克斯韦，他发现双耳效应，瑞利散射(解释天空蓝色)，发现惰性气体(诺奖)，瑞利-金斯公式(紫外灾难)。
首先是伦琴因为发现X射线而得到第一个诺奖，后面很多实验物理学家都想去发现新的射线；贝克勒尔(磷光和荧光研究的专家)发现了天然放射性，三代都在研究长余辉，下雨天把铀岩放在家里的胶片上，因而发现了天然放射性；居里夫妇也发现了天然放射性，而且发现了新的元素，1903年贝克勒尔和居里夫妇共同获得了诺贝尔物理学奖。
原子稳定性：根据卢瑟福模型，电子是带电的，根据经典的电磁学理论，一个做圆周运动的电子会产生交变的电磁场，这个电磁场会让它不停地辐射电磁波，电磁波是能量，即不断损耗能量，最终电子会撞向原子核才对。
量子力学人物
普朗克：量子之父，1889年前往柏林洪堡大学，接手基尔霍夫的黑体辐射的研究工作。他发现维恩位移不适合低频辐射的情况，他假定处于辐射场中的电偶极振子的能量是一份一份的，每份的大小正比于振动的频率。在此基础上，发现了黑体辐射定律。可惜的是，普朗克推开了量子力学的大门，之后却又回到了经典力学。
爱因斯坦：
(1) 光电效应：1905年，爱因斯坦看透了这个为人熟知的公式，发现了它后面隐藏的量子。通过和经典气体的熵类比，爱因斯坦发现黑体辐射可以看作是一种特殊的由 “光子”构成的气体，每个光子的能量是\(h \nu\)，“粒子和波的行为有本质的不同，光虽然被广泛认为是一种波，但在很多现象里，比如黑体辐射、荧光、和光致阴极辐射，光的行为更像粒子。”他用光量子的概念轻松地解释了光电效应。在当时的物理学 界，所有的人都认为光不是粒子，而是一种波——按照麦克斯韦方程振动和传播的电磁波。
(2) 固体比热：他将普朗克的黑体辐射公式应用固体比热。爱因斯坦认为固体中原子振动的能量也是一份一份的，它们应该同样遵守普朗克的黑体辐射公式。当时物理学家已经将温度降到摄氏−250度，他们在实验中发现固体比热会随着温度降低大幅减小。经典理论完全无法解释这个现象。爱因斯坦利用普朗克的公式发现，固体的比热确实会随温度降低而减小，而且自己推导出来的公式和已经发表的实验结果吻合得非常好。
波尔：书香门第，被卢瑟福原子模型吸引，思索该如何嵌入电子得到一个稳定的原子模型。认为为了让原子稳定，必须引入量子的概念。爱因斯坦曾利用量子来描述固体中原子的振动，现在玻尔用量子来描述原子的内部结构，这是一个里程碑式的进展。
不足之处：无法描述谱线的强度，也不能预测氢原子中释放出来的光子的偏振，后面他用了半直觉的对应原理解释了。
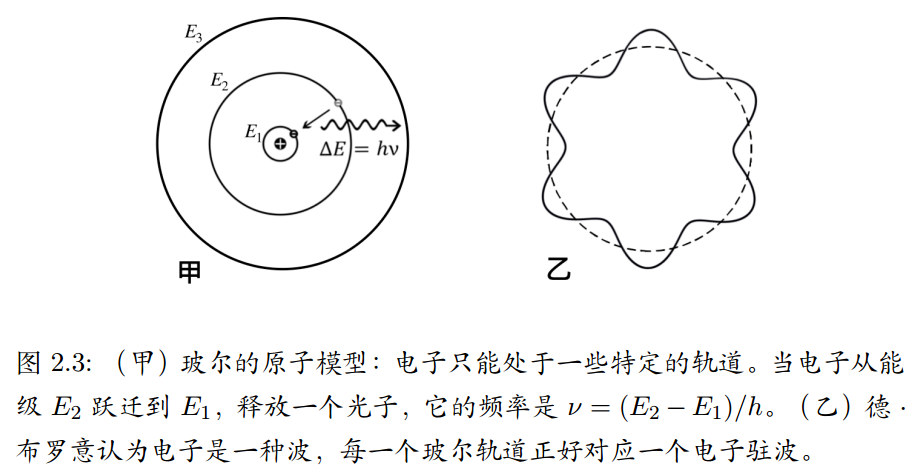
索末菲：很快推广了玻尔的理论，他认为任何物理体系都可能处于分立的“稳态”，并且给出了更一般的“量子化”规则。利用这个推广的理论，索末菲发现原子中的电子应该具有三个量子数而不是玻尔理论中的一个，并且他的量子理论可以解释更多的和原子相关的现象，比如斯塔克效应，塞曼分裂(扩充)等。
不足之处：玻尔-索末菲理论不能描述任何具有两个或两个以上电子的原子或分子。
例如，它无法给出氦原子的谱线，不能描述分子间的共价键。
注：
(1) 索末菲是目前为止教导过最多诺贝尔物理学奖得主的人，他首先提出第二量子数(角量子数)和第四量子数(自旋量子数)，并且提出精细结构常数和开创了X射线波动理论。他学生中最有名的就是海森堡和泡利了，还有德拜(亚琛时期)，鲍林。
(2) 桃李满天下为大师之师，无缘于诺奖成无冕之王-张天蓉
波色：印度本土培养的物理学家，在他的黑体辐射推导里又引入了一个新的完全突破经典的概念，光子是完全相同、不可区分的。基于这个概念再利用光量子，玻色在人类历史上第一次给出了黑体辐射公式的正确推导。玻色的突破是惊世骇俗的。在这之前没有任何人意识到了量子物理和经典物理会有这种本质区别：在量子的世界里，相同是绝对的；在经典的世界里，相同只是一种近似。
注：
(1) 他给爱因斯坦的信“我成功地推导出来了普朗克公式中的系数\(8 \pi \nu^{2} / c^{3}\)。在推导中没有用经典电动力学，而是假设相空间应该被分成很多小格每格大小是\(h^{3}\)。”
(2) 爱因斯坦立刻将波色全同这个概念推广，既然光子是全同的、不可区分，那么其他粒子也是一样的。爱因斯坦为此连续发表了三篇论文，在这些论文里爱因斯坦预言了著名的玻色-爱因斯坦凝聚现象。七十年后，1995年物理学家利用超冷原子气验证了爱因斯坦的预言。
海森堡：他发现这些可观测量依赖于两个指标，它们的乘法是不对易的。他自己也不清楚这些变量是什么，对自己的新理论框架并没有太多信心。但是玻恩(程开甲和彭恒武在爱丁堡大学的博士导师)立刻看出了海森堡工作的重要性，并很快意识到海森堡提出的这些古怪的可观测量其实就是数学上的矩阵，后面他们就共同发表了相关论文。清楚地给出了矩阵力学的基本框架。到1926年初，泡利(海森堡的师兄，两个好基友)和狄拉克各自独立地在矩阵力学的框架内给出了氢原子的能级。
20 岁时，海森堡勇敢地引入了半整量子数(在索末菲研讨班上提出的)；24岁时，海森堡勇敢地突破了旧的量子理论，创立了矩阵力学。
泡利：奥地利小天才，电子为什么不聚集到最低的能级上？这个问题从此一直萦绕在 泡利的脑海。泡利在1925年把这个问题想清楚了，为了解释元素周期表，必须做两个假设：
(1) 除了空间自由度外，电子还有有一个奇怪的自由度；
(2) 任何两个电子不能同时处于完全相同的量子态。
第一个假设很快被证实，这个奇怪的自由度就是自旋。第二个假设现在被叫做泡利不相容原理。
德布罗意：法国贵族，博士论文是关于德布罗意波，爱因斯坦立刻洞察到了德布罗意工作的重要性。当时绝大多数物理学家依然拒绝接受爱因斯坦的观点(虽然已经有实验证实)，光是粒子。原因很简单，大量的实验和麦克斯韦方程告诉我们光是波。同一种东西怎么可能既是波又是粒子呢？波的光可以是粒子，于是德布罗意认为粒子比如电子也可以是波，那么电子围绕质子就会形成驻波。依照这个思路，德布罗意神奇地重新推导出了玻尔的氢原子轨道和能级。他语言预言电子也会发生散射和干涉，后面实验也证实了。
薛定谔：他的灵感来自德·布罗意的波粒二象性，既然粒子是波，那么就应该有一个相应的波动方程。1926年薛定谔提出了他那著名的波动方程和波函数，并利用它们给出了氢原子的正确能级。他的书《什么是生命》在生物界也影响广泛 。
狄拉克：英国物理学家，狄拉克性格孤僻、少言寡语、不善于和别人交流，为此留下了很多趣闻轶事。为整个新量子理论框架填上点睛之笔的是狄拉克。当他读过薛定谔的论文后，狄拉克很快意识到薛定谔的波动力学和海森堡的矩阵力学的等价性。在这篇论文里，狄拉克不但清晰地论述了薛定谔和海森堡理论的等价性，而且通过多粒子波函数的置换对称性明确指出量子世界里只有两种粒子，玻色子和费米子。
注：
(1) 他1930年写的专著《量子力学原理》(The Principles of Quantum Mechanics) 时至今日依然没有过时，是每个物理系学生的必读。
(2) 他通过量子力学和狭义相对论结合，提出了一个新的波动方程，狄拉克方程，预言了反粒子的存在。
(3) 发现分析力学的泊松括号和海森堡矩阵力学的PQ-QP很像，于是基于此提出了正则量子化。
费米：李政道的导师，实验和理论都好，费米也是一个难得的天才，几乎是自学成才。和狄拉克不一样，费米善于和人交流，更注重物理的直觉而不是数学的优美。后来费米在粒子物理方面做出了很多杰出的贡献，比如搭建了第一个核反应堆，领导了曼哈顿计划。
量子力学概念
哥本哈根诠释：哥本哈根诠释包含了几个重要的观点
(1) 一个量子系统的量子态可以用波函数来完全地表述。波函数代表一个观察者对于量子系统所知道的全部信息。
(2) 按照玻恩定则，量子系统的描述是概率性的。一个事件的概率是波函数的绝对值平方。(马克斯·玻恩)
(3) 不确定性原理阐明，在量子系统里，一个粒子的位置和动量无法同时被确定。(海森堡)
(4) 物质具有波粒二象性；根据互补原理，一个实验可以展示出物质的粒子行为，或波动行为；但不能同时展示出两种行为。(尼尔斯·玻尔)
(5) 测量仪器是经典仪器，只能测量经典性质，像位置，动量等等。
(6) 对应原理：大尺度宏观系统的量子物理行为应该近似于经典行为。(尼尔斯·玻尔与海森堡)
这一切告诉我们一个明确的道理：科学的突破是没有固定模式的。
哥本哈根学派解释的核心：波尔的互补原理，电子的波动性和粒子性在同一时刻是互斥的，但它们在更高的层次上是统一在一起的，作为电子的两面被纳入一个整体概念中；电子表现出波动性还是粒子性取决于你用什么方法去探测它。它连通波恩的概率解释，海森堡的不确定性，三者共同构成了量子力学的“哥本哈根解释”的核心。
对应原理：
互补原理：The particle and the wave models are complementary. No measurements can simultaneously reveal the particle and the wave properties of matter.
旧量子力学：普朗克黑体辐射公式的推导是错的；爱因斯坦固体比热理论是通过类比得到的，非常不严谨；玻尔几乎是用一种拼凑的方式得到了氢原子的能级。这些缺点让年长的物理学家非常不舒服，他们选择了回避和不参与。年轻的一代虽然也知道这些缺陷，但他们更看重积极的一面：(1) 和实验结果吻合；(2) 经典理论不可能解释这些实验结果。
基尔霍夫辐射定律：黑体是基尔霍夫提出的概念，在相同的温度下，各种不同物体对相同波长的单色辐出度与单色吸收之比都相等，并等于该温度下黑体对同一波长的单色辐出度。 (好的吸收体也是好的辐射体) $$\displaystyle\frac{M_{\lambda 1}(T)}{a_{\lambda 1}(T)}=\frac{M_{\lambda 2}(T)}{a_{\lambda 2}(T)}=\cdots=M_{\lambda 0}(T)$$
维恩位移定律：是物理学上描述黑体电磁辐射光谱辐射度的峰值波长与自身温度之间反比关系的定律 \(\lambda_{\max }=\displaystyle\frac{b}{T}\)
爱因斯坦奇迹年：指的是阿尔伯特·爱因斯坦在公元1905年在德国科学期刊《物理年鉴》所发表的四篇论文。这四篇论文推进了近代物理学的基础，并且让人重新理解空间、时间、质量与能量。公元1905年也因此被称为爱因斯坦奇迹年。第一篇论文解释了光电效应，第二篇论文解释了布朗运动，第三篇论文介绍了狭义相对论，第四篇论文介绍了质能等价。
第一届索尔维会议：1911年在布鲁塞尔召开，大会题目是《辐射和量子》(Radiation and the Quanta)。洛伦兹是大会主席，爱因斯坦应邀参加，报告的题目是《比热问题》(The problems of specifc heat)。
两朵乌云：以太问题和统计力学中的能量均分定理可能会被打破，或者说比热问题(注意不是不是黑体辐射)。对应的实验分别是迈克逊莫雷光速恒定实验，第二个对应的是黑体辐射。两朵乌云后面都张成了参天大树，分别是相对论和量子论。
玻尔-范卢文定理：when statistical mechanics and classical mechanics are applied consistently, the thermal average of the magnetization is always zero.This makes magnetism in solids solely a quantum mechanical effect and means that classical physics cannot account for paramagnetism, diamagnetism and ferromagnetism. Inability of classical physics to explain triboelectricity also stems from the Bohr–Van Leeuwen theorem.
量子：量子的英文是quantum，源自拉丁文quantus，它的原义是“多少”。量子现在是一个物理专业名词，它是场的最小激发。比如，电磁场的最小激发是光子，即电磁场的量子是光子。所有的基本粒子都是某个场的量子（最小激发）。除了光子，这些量子（最小激发）还包括电子、夸克、中微子、胶子等。质子不是量子，因为质子是由夸克构成的复合粒子。同理氢原子不是量子。
海森堡不确定性原理：由于海森堡不确定性原理，一个原子在绝对零度（自然允许的最低温度）时也不会被完全“冻”住。如果原子完全“冻”住不动了，那它的位置就确定了，速度是零所以也是确定的。这违反海森堡不确定性原理，因此世界上没有完全静止的原子。即使在绝对零度，原子也会振动。物理学家把这种振动叫做零点振动。氦原子的零点振动尤其显著，以至于氦在绝对零度仍然处于液体状态。在绝对零度时，只有氦还能处于液态，所有其他物质都会变成固体。
态叠加原理：量子力学描述的世界里，一个物体可以同时处于两个不同的地点或具有不同的速度。比如氢原子中的电子可以同时处于质子的左边和右边，电子还可以同时绕着质子顺时针转和逆时针转。
量子随机性 - 假设有一个粒子，它处于一个位置的叠加态，即它同时处于A点和B点。现在我们对它的位置进行测量，确认它到底位于何处。量子力学告诉我们测量结果是随机的：可能是A也可能是B。但这种随机性和日常生活中遇到的随机现象有根本的不同。在量子力学里，测量结果的随机性是内在的，源自上面提到的态叠加原理。
量子全同性：量子力学里，相同是绝对的。两个电子是相同的，你不可能用任何方法把它们区分开；两个光子是相同的，你不可能用任何方法把它们区分开。两个光子也既是频率不同，也属于全同粒子。为了强调这种绝对的相同，在量子力学里，我们称电子是全同的，光子是全同的。对于普通的硬币，四种可能性中的每种出现的几率是 1/4，所以一枚硬币朝上一枚硬币朝下出现的几率是1/2。但对于全同的量子硬币，一 枚硬币朝上一枚硬币朝下出现的几率是1/3或者1（因为有些情况下，两枚全同的硬币不允许同时向上或向下）
全同粒子可以分为两种类型：
(1) 玻色子可以处于同样的量子态。光子、胶子、声子、与氦-4原子，都是玻色子。
(2) 费米子不能处于同样的量子态（这性质称为泡利不相容原理）。电子、中微子、夸克、质子、中子、氦-3原子，都是费米子。
玻色子满足玻色-爱因斯坦统计：同一个量子态可以被多个玻色子占据；费米子满足费米-狄拉克统计： 一个量子态最多只能被一个费米子占据。
量子纠缠：当你匆忙出门旅行，到达目的地后发现包里只有一只右手手套。无论你离家多远，你立刻知道被遗忘在家里的那只手套是左手的。为了方便起见我们把它叫做超距关联。超距是个物理名词，用来描述不需要花费时间就可以穿越任何空间距离的现象。这种超距关联发生的前提条件是，我们事先掌握事情的整体情况：一副手套总是有一只左手手套和一只右手手套；清朝皇帝颁布的法律无条件在整个大清帝国立刻生效。量子世界里也有类似的超距关联，物理学家把它称作量子纠缠。贝尔发现(实验后面也证实了)经典超距关联总是满足这个不等式；而量子纠缠则可以违反这个不等式。除了超距关联，量子纠缠还有一个惊人的特征：纠缠的粒子会失去自我。
量子计算机：科学家发现量子计算机可能比经典计算机更强大。但是迄今科学家只能展示量子计算机在整数因子分解、随机搜索等少数问题上比经典计算机优越，科学家也并不完全清楚量子计算机为什么比经典计算机强大。
隐性量子技术：，实现的功能原则上可以用经典技术实现，只是量子力学的出现使这类技术变得更小更快更精。比如硬盘的信息存储；
显性量子技术：实现的功能原则上无法用非量子技术（或经典技术）实现，比如量子通信的远程密钥分配和量子计算机里的某些逻辑门。量子力学是个台前台后的英雄，前面提到的量子力学的特征，特别是态叠加原理、量子随机性、和量子纠缠，在显性量子技术实现的功能里会直接体现出来。
不存在一个量子态，同时是位置算符和动量算符的本征态。海森堡不确定性来源于算符的不可对易性，和测量本身没有关系。当然测量本身也会对粒子产生影响，比如要想测某个粒子的位置，就得用光来测(观察)，那么光必然在测试过程中对该粒子产生影响，这就是测量对系统的扰动。
波包塌缩 vs 多世界理论，没有办法通过实验判定哪个是对的。
相空间
对于普通的物体，动量和速度是两个完全等价的概念。但是对于物理学家，动量这个概念更基本，因为对于无静止质量的粒子动量和速度是非常不一样的。比如光子，不同频率的光子的速度大小都是一样的，即光速，但它们可以具有不同的动量。利用动量，我们可以将动能重写为\(K=p^{2} /(2 m)\)。现代物理学家非常喜欢把能量\( E\)的表达式叫做哈密顿量（Hamiltonian）通常用\(H\)来表示，即写成$$H=\frac{p^{2}}{2 m}+V(x)$$喜欢的理由有很多个，其中非常重要的一个理由是哈密顿量在量子力学中扮演非常关键的角色，后面我们会看到。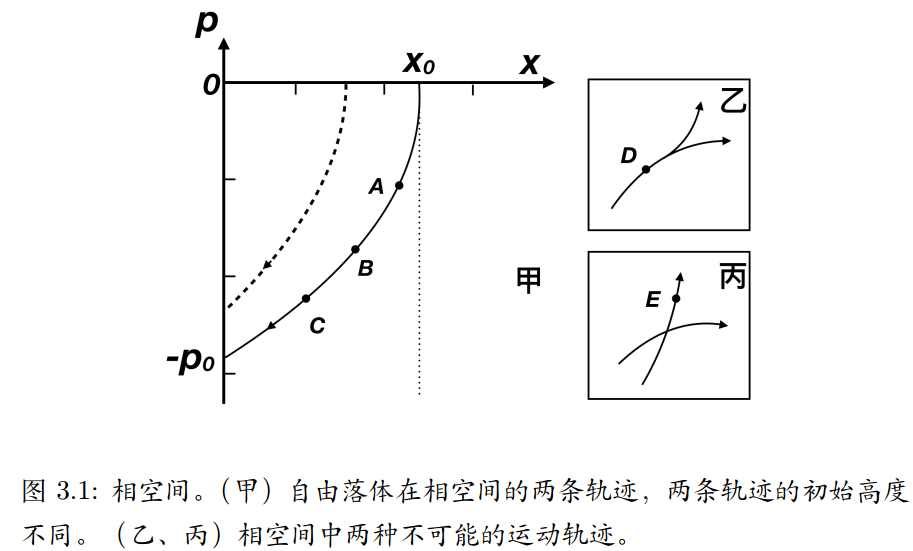
以动量和位置分别为竖轴和横轴构成的空间叫做相空间。相空间里的每个点有确定的坐标和动量，对应一个运动状态。能量守恒有\(p^{2} /(2 m)+m g x=E\)，\( E\)是系统的总能量。对应每一个位置\(x\)，我们有一个确定的动量$$p=-\sqrt{2 m E-2 m^{2} g x}$$上面这个公式代表相空间中的一条运动轨迹。由于能量守恒相空间里的一条运动轨迹上每个点对应的能量一定相同，所以这些轨迹也被称为等能线。由于\(E\)可以连续变化，轨迹可以连续在相空间改变。由B可以反推A，也可以预测一定要到C，它的过去和将来都是确定的：我们既可以回推过去发生的故事也可以准确预测未来。 右侧的图分叉表示不可预测或反推，存在多种可能性。
将相空间用于一维简谐振子$$x=x_{0} \cos (\omega t), \quad p=-p_{0} \sin (\omega t)$$速度 \(v=\displaystyle\frac{d x}{d t}=-x_{0} \omega \sin (\omega t)\)
受力 \(F=\displaystyle\frac{d p}{d t}=-p_{0} \omega \cos (\omega t)=-p_{0} \omega x / x_{0}=-m \omega^{2} x\)
根据\( \sin ^{2} \theta+\cos ^{2} \theta=1\)有\(\displaystyle\frac{p^{2}}{p_{0}^{2}}+\displaystyle\frac{x^{2}}{x_{0}^{2}}=1\)(椭圆)将\(p_{0}=m x_{0} \omega\)带入有$$\frac{p^{2}}{2 m}+\frac{1}{2} m \omega^{2} x^{2}=\frac{1}{2} m \omega^{2} x_{0}^{2}$$ 等式右边是一个能量常数，所以上式表示简谐振子的能量守恒。而左边就是简谐振子的哈密顿量$$H=\frac{p^{2}}{2 m}+\frac{1}{2} m \omega^{2} x^{2}$$其中\( V(x)=\displaystyle\frac{1}{2} m \omega^{2} x^{2} \)是简谐振子的势能。
旧量子力学
对于前面的简谐振子模型，经典力学认为\(x_{0}\)是连续的，可以从零到无穷大，相应的轨迹会充满整个相空间。根据玻尔和索末菲发展出来的旧量子理论，只有一些满足量子化规则的轨道(在量子力学里，人们习惯把轨迹称作轨道)才是允许的。
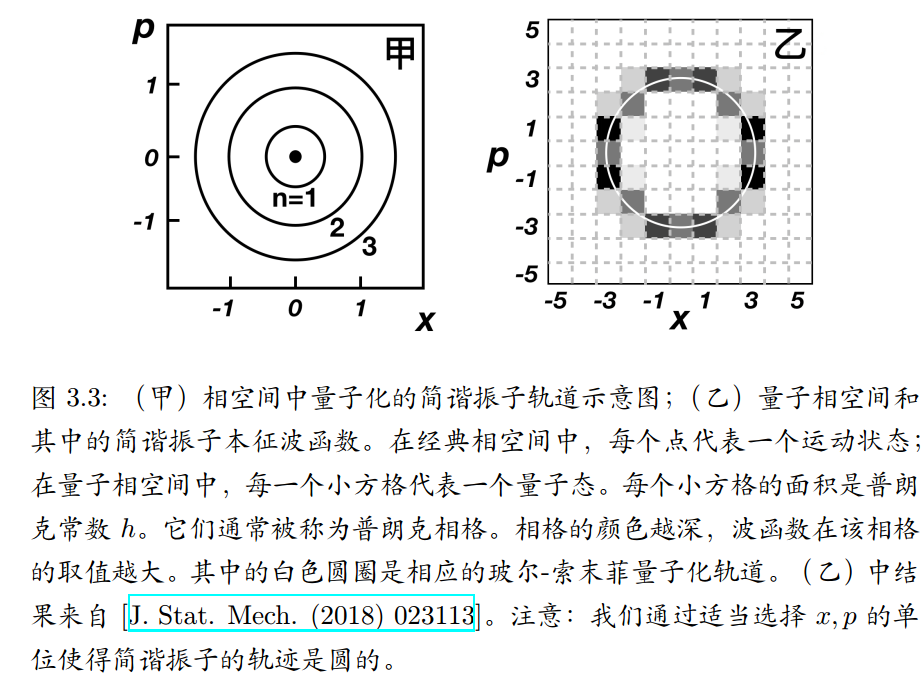玻尔和索末菲的量子化规则是：量子化轨道在相空间围出的面积\(S\)是普朗克常数\( h\)的整数倍，即$$S=\oint p d x=n h, \quad n=1,2,3, \cdots$$应用到简谐振子，对于一个给定的\(x_0\)其对应轨迹围成的面积是$$S=\pi p_{0} x_{0}=\pi m x_{0}^{2} \omega=2 \pi E / \omega$$这里\(E=m x_{0}^{2} \omega^{2} / 2 \)是振子能量。如果这个\(x_0\)对应第\(n \)个量子化的能级\(E_n\)，那么我们应该有$$2 \pi E_{n} / \omega=n h$$ 我们于是得到量子化的简谐振子能级(\( h=2 \pi \hbar\))$$E_{n}=n \hbar \omega$$每个离散的能级\(E_n\)，在相空间都对应有一条经典轨迹。把玻尔和索末菲的量子化规则应用到氢原子就能得到氢原子的能级和量子化轨道。
在现代量子理论里，可以通过求解薛定谔方程来获得能级，每个能级对应一个本征波函数。依然用简谐振子作为例子。按照现代量子理论，用薛定谔方程计算出来的能级是$$E_{n}=\left(n+\frac{1}{2}\right) \hbar \omega \quad n=0,1,2, \cdots$$和旧量子力学理论相差\( \hbar \omega / 2\)，差异原因不在该书范围。上面右图，一个粒子不能同时具有确定的动量和位置，所以一个量子态不再对应相空间的一个点，而是对应一个小方格，方格的大小是普朗克常数，格子颜色越深波函数取值越大，是新量子论。
线性代数汇总
厄密共轭： 一个矩阵\(M\)的厄密共轭不但将它的行和列相互调换，而且还取
复共轭，记作\(M^{\dagger}\)$$\left(\begin{array}{ccc} 1 & 2 & 3 \\ i & 2 i & 3 i \\ 4 & 5 & 6 \end{array}\right)=\left(\begin{array}{ccc} 1 & -i & 4 \\ 2 & -2 i & 5 \\ 3 & -3 i & 6 \end{array}\right)^{\dagger}$$
对角矩阵： 对角矩阵间的乘法是可以交换的\(M_{1} M_{2}=M_{2} M_{1}\)$$\left(\begin{array}{lll} 1 & 0 & 0 \\ 0 & 3 & 0 \\ 0 & 0 & 8 \end{array}\right)$$
厄密矩阵：如果一个矩阵\(M\)满足\(M=M^{\dagger}\)，这个矩阵叫厄密矩阵。下面三个矩阵都是厄密矩阵(人们通常称这三个矩阵为泡利矩阵。显然实的对称矩阵(所有矩阵元 都是实数)是厄密矩阵)$$\hat{\sigma}_{x}=\left(\begin{array}{ll} 0 & 1 \\ 1 & 0 \end{array}\right), \quad \hat{\sigma}_{y}=\left(\begin{array}{cc} 0 & -i \\ i & 0 \end{array}\right), \quad \hat{\sigma}_{z}=\left(\begin{array}{cc} 1 & 0 \\ 0 & -1 \end{array}\right)$$
幺正矩阵： 如果矩阵\(M\)满足\(M^{\dagger} M=M M^{\dagger}=I\)，这种矩阵叫幺正矩阵。下面是一个幺正矩阵$$\left(\begin{array}{cc} \cos \theta & i \sin \theta \\ i \sin \theta & \cos \theta \end{array}\right)$$
在量子力学里，人们主要关心厄密矩阵的本征向量和本征值。由于在量子力学中本征向量对应一个量子态，物理学家喜欢把本征向量称作为本征态。对于任意一个\(n \times n\)的矩阵\( O \)
(1) \(O \)一定有\( n \) 个本征态\(\left|\phi_{1}\right\rangle,\left|\phi_{2}\right\rangle, \cdots,\left|\phi_{n}\right\rangle\), 其相应本征值为\(v_{1}, v_{2}, \cdots, v_{n}\)。 即\( O\left|\phi_{j}\right\rangle=v_{j}\left|\phi_{j}\right\rangle, \quad(j=1,2, \cdots, n)\) 。
(2) 可以证明本征值\(v_{1}, v_{2}, \cdots, v_{n}\)都是实数。
(3) 可以证明本征态\( \left|\phi_{1}\right\rangle,\left|\phi_{2}\right\rangle, \cdots,\left|\phi_{n}\right\rangle \) 相互正交，即\(\left\langle\phi_{i} \mid \phi_{j}\right\rangle=0,(i \neq j)\)。
(4) 由于\(c\left|v_{j}\right\rangle\)依然是本征态，我们可以利用这个性质，通过适当选择\(c\)使得\(\left\langle\phi_{j} \mid \phi_{j}\right\rangle=1\)。这种本征态被称作是归一的。
(5) 有可能某两个本征值\(v_{i}=v_{j}(i \neq j) \)，这说明相对应的两个本征态\( \left|\phi_{i}\right\rangle\)和\(\left|\phi_{j}\right\rangle \)简并。
直积空间：两个希尔伯特空间可以构成一个新的希尔伯特空间\(V=V_{1} \otimes V_{2}\)，这种运算叫直积，直积空间的维数\( n=n_{1} n_{2}\)。直积空间\(V\)的向量为\(|\phi\rangle \otimes|\varphi\rangle\)，等式右侧直积符号前后的向量分别来自\( V_{1} \)和\(V_{2}\)空间。积空间\(V\) 中的向量总是可以表达成\( V_{1} \)和\(V_{2}\)中向量的直积或多个直积的线性叠加，即$$|\Psi\rangle=c_{1}\left|\phi_{1}\right\rangle \otimes\left|\varphi_{1}\right\rangle+c_{2}\left|\phi_{2}\right\rangle \otimes\left|\varphi_{2}\right\rangle+\cdots+c_{j}\left|\phi_{j}\right\rangle \otimes\left|\varphi_{j}\right\rangle+\cdots$$
直积规则和普通乘法非常类似$$\begin{aligned} &\left(\left|\phi_{1}\right\rangle+\left|\phi_{2}\right\rangle\right) \otimes\left(\left|\varphi_{1}\right\rangle+\left|\varphi_{2}\right\rangle\right) \\ =&\left|\phi_{1}\right\rangle \otimes\left|\varphi_{1}\right\rangle+\left|\phi_{1}\right\rangle \otimes\left|\varphi_{2}\right\rangle+\left|\phi_{2}\right\rangle \otimes\left|\varphi_{1}\right\rangle+\left|\phi_{2}\right\rangle \otimes\left|\varphi_{2}\right\rangle \end{aligned}$$一个特例\( \left(\left|\phi_{1}\right\rangle+\left|\phi_{2}\right\rangle\right) \otimes|\varphi\rangle=\left|\phi_{1}\right\rangle \otimes|\varphi\rangle+\left|\phi_{2}\right\rangle \otimes|\varphi\rangle\)
不可交换性 \(|\phi\rangle \otimes|\varphi\rangle \neq|\varphi\rangle \otimes|\phi\rangle\)
标量相乘 \(c|\phi\rangle \otimes|\varphi\rangle=|\phi\rangle \otimes c|\varphi\rangle\)
在量子力学中我们经常遇到多个系统组成的复合系统，复合系统的希尔伯特空间就是各个子系统希尔伯特空间的直积。
迈入量子之门
施特恩-格拉赫实验
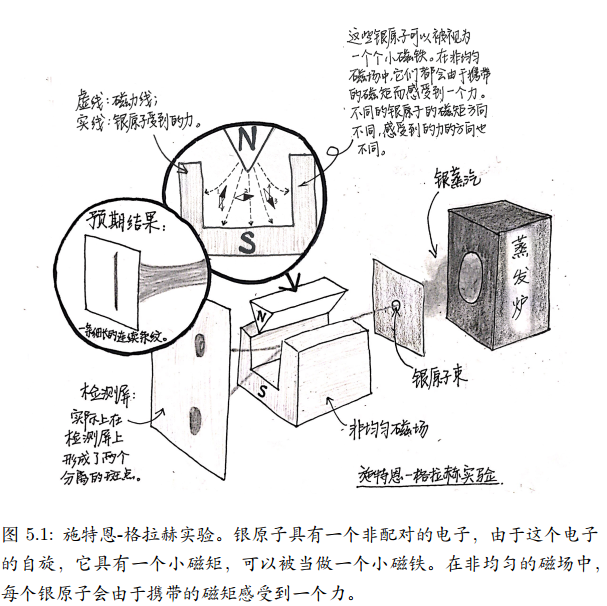1922年，两位德国物理学家的实验，高温炉将银加热蒸发成气体，银蒸汽从炉子里出来经过一些控制阀门形成银原子束，银原子束通过一个非均匀磁场后到达检测屏。他们发现银原子束会被非均匀磁场折射分解成两束，最后在检测屏上形成两个分离的斑点。这个结果完全出乎施特恩和格拉赫的预料。因为根据经典物理，他们预期观察到一条细长的连续条纹。
每个银原子携带磁矩，可以被看作一个小磁铁，在均匀磁场中，南北两极受到的力大小相同方向相反，银原子作为一个整体不会感受到任何力。实验中的磁场是不均匀的，这样南北两极受到的力大小不同，银原子会总体感受到一个力，运动轨迹则因此会发生偏折。这个偏折力的大小和方向取决于磁矩的方向和磁场方向的夹角：夹角越小、偏折力越强、偏折角度越大；如果两个银原子的磁矩正好相反(比如图中的银原子 1和银原子3)，它们感受到的力正好相反，它们的偏折方向会因此而相反。由于银原子来自高温炉产生的银蒸汽，它们的磁矩方向是随机的，指向任何一个方向的概率是相同的，这也意味着这些银原子感受到的偏折力会是一个均匀分布。所以，按照经典物理，预期的观察结果应该是一条细长的条纹。但是，实验结果却是两个分立的斑点。
这个实验结果就像有个人在掷一个有无穷个面的骰子(这实质上就是一个球)，但每次投掷完后只会出现1或2。这怎么可能？银原子一定被人装了什么机关！这个机关就是量子力学。银原子具有一个完全无法用经典力学描述的自由度，自旋。银原子具有磁矩，就是因为它带自旋。虽然自旋可以在空间指向任意方向，但按照量子力学，你的测量结果只可能有两个，因此图中的测屏上只可能有两个斑点。
注意：如果将磁场沿着轴线转动90度，那么同样可以得到两个斑点，只是分布在屏幕左右两侧，而不是之前的上下两侧。这说明在任何方向上都有两个自旋。参考：量子故事会（8）量子力学陷入困境被逼无奈引入自旋
银原子基态轨道角动量为0, 所以没有轨道磁矩。入射银原子束分成两束又表明银原子的确具有磁矩, 这个磁矩并非来自电子轨道, 而是来自于电子自己本身 (核磁矩要比电子磁矩小三个量级左右)。这个磁矩是电子内禀性质, 而电子自旋相联系。 虽然所有教科书都用斯特恩 -盖拉赫实验说明电子具有自旋且自旋角动量是1 / 2, 但真实的历史并非如此。斯特恩和盖拉赫在 1922年时根本就不知晓 “自旋” 概念, 他 们做实验的动机和目标也不是测量自旋(而是测轨道角动量量子化？)。记得我们曾经提过: 几乎所有重大的物理发 现都是 “副产品”。银原子双斑实质上是寻找芝麻过程中大自然给我们的西瓜, 然而大部分情况下我们都是丢掉西瓜去捡芝麻。参考这里。
自旋
地球自转和公转(自转)，都有一个角动量。物理学家把这种由于物体的空间旋转而形成的角动量叫做轨道角动量，而把自旋叫做内禀角动量，以示区别。在经典物理中，物体只能有轨道角动量；在量子物理中，一个粒子或物体可以既有轨道角动量又有自旋。我们必须用量子力学才能描述自旋。当一个带电粒子旋转时，它具有轨道角动量，并形成磁矩，这时候这个粒子就像一个小小 的指南针。当一个粒子具有自旋时，它也会具有磁矩。正由于这个性质，我们大致可以把自旋类比成一个很小的指南针。这种类比不严格，但能帮助我 们建立一些直观的理解。
- 自旋是微观粒子的一个内禀特征，和静止质量和电荷类似。但自旋的内涵要 丰富得多，因为它还是一种自由度(抽象空间的自由度，在经典力学中完全不存在)。
- 轨道角动量总是普朗克常数的整数倍\(m \hbar\)，\(m\)整数可正可负。
- 自旋对应的角动量则可以是\(\pm \hbar / 2, \pm \hbar, \pm 3 \hbar / 2\)。
- 自旋 1/2 指的就是这个自旋的最大角动量是\(\hbar / 2\)。质子和中子 的自旋也是 1/2。光子的自旋则是 1(实际取值只能是±1，不能取)，这意味着光子自旋的最大角动量是\(\hbar\)。
- 自旋还和费米子、玻色子紧密相关：费米子的自旋都是半整 数的，比如 1/2， 3/2， 5/2 等；玻色子的自旋都是整数的，比如 0， 1， 2 等。
- 狄拉克发现电子具有自旋 1/2 是狭义相对论和量子力 学结合的必然结果。
(1) 在量子力学中，自旋是粒子所具有的内禀性质，其运算规则类似于经典力学的角动量，并因此产生一个磁场。虽然有时会与经典力学中的自转（例如行星公转时同时进行的自转）相类比，但实际上本质是迥异的。经典概念中的自转，是物体对于其质心的旋转，比如地球每日的自转是顺着一个通过地心的极轴所作的转动。地球自转并不是内在性质。如果地球不转了,它还是地球,但是粒子如果自旋不一样,它就是一个新粒子。 粒子的自旋——是你不能想象的事情！
量子力学里的几率是本质的，这是量子力学的基本原则。量子力学中，运动状态是希尔伯特空间中的一个向量；可观测量 是算符（或矩阵）；观测结果则是算符的本征值。