纠错,一些补充
传统傅里叶变换所存在的问题
我们把我们前面学习的傅里叶变换称为“传统的傅里叶变换”。按照我们原来的理论,只有函数的积分收敛了,它才能进行傅里叶变换(有点类似我们的波函数必须是在希尔伯特空间中)。如此一来,对于常规的\( \sin \),\( \cos \),常数函数等无法进行傅里叶变换,因此我们需要一个更鲁棒的傅里叶变换,使之能处理这些常规函数。
原本的傅里叶变换之所以无法应用到这些常规函数,问题的关键在于积分的收敛性。
传统的傅里叶变换主要有两个问题:
1. 傅里叶变换基于积分的收敛;
2. 傅里叶逆变换必须可行,否则正变换被执行了也毫无意义。
注:鲁棒是Robust的音译,也就是健壮和强壮的意思。 它也是在异常和危险情况下系统生存的能力。 比如说,计算机软件在输入错误、磁盘故障、网络过载或有意攻击情况下,能否不死机、不崩溃,就是该软件的鲁棒性。 所谓“鲁棒性”,也是指控制系统在一定(结构,大小)的参数摄动下,维持其它某些性能的特性。
问题例子1$$\quad \quad \quad \quad \quad \quad \quad \quad f(t)=\Pi(t)\\ \begin{array}{lc} \mathcal{F} \Pi=\operatorname{sinc} & \mathcal{F} \Pi=\displaystyle\int_{-\infty}^{\infty} e^{-2 \pi i s t} d s \\ \mathcal{F}^{-1} \operatorname{sinc}=\mathcal{F}^{-1} \mathcal{F} \Pi=\Pi & \quad \mathcal{F}^{-1} \operatorname{sinc}=\displaystyle\int_{-\infty}^{\infty} e^{2 \pi i s t} \displaystyle\frac{\sin \pi s}{\pi s} d s \\ \mathcal{F} \operatorname{sinc}=\mathcal{F} \mathcal{F} \Pi=\Pi^{-}=\Pi & \quad \mathcal{F} \operatorname{sinc}=\displaystyle\int_{-\infty}^{\infty} e^{-2 \pi i s t} \displaystyle\frac{\sin \pi s}{\pi s} d s \end{array}$$对于\( f(t)=\Pi(t)\),我们可以通过傅里叶逆变换、对偶定理等得到简介的结果,但是在实际的计算机操作中,我在对原始信号进行傅里叶变换之后,需要用右侧的等式进行逆变换还原信号的操作,但是\( \mathcal{F}^{-1} \operatorname{sinc}\)和\(\mathcal{F} \operatorname{sinc} \)的积分求法是非常困难的,而且要处理收敛性问题,即两侧对称的跳变点(通常取跳变前后的均值)。
对于最简单的\(\Pi \)函数都出现了这样的问题,需要特殊的技巧进行特殊的讨论,这使得我们对传统的傅里叶变换的适用性产生了怀疑。
问题例子2$$\begin{array}{ll} f(t)=1 & \mathcal{F} f(s)=\displaystyle\int_{-\infty}^{\infty} e^{-2 \pi i s t} d t \\ f(t)=\sin 2 \pi t & \mathcal{F} f(s)=\displaystyle\int_{-\infty}^{\infty} e^{-2 \pi i s t} \sin 2 \pi t d t \\ f(t)=\cos 2 \pi t & \mathcal{F} f(s)=\displaystyle\int_{-\infty}^{\infty} e^{-2 \pi i s t} \cos 2 \pi t d t \end{array}$$对于这些不收敛的函数的积分是无意义的,因为\( e\)的复指数项是振荡的,所以不可能收敛。
处理这些问题的方法:
有两种方法可以处理这些问题:
1. 针对特殊函数进行特殊的研究
2. 从基础重新研究傅里叶变换,得到一个更鲁棒的、能适用各种函数的新傅里叶变换的定义(rework the foundation and definition, new conception of convergence,均方收敛(我们在\( L^{2} \)积分那里有谈到,其实就是希尔伯特空间的函数特性),而不是点收敛)。 在\(1940 \)年代以前,各种数学家、科学家们都是采用第一种方法,对各种各样的函数进行研究。\( 40\)年代以后,科学家们开始采用第二种方法,这种方法发展至今已经相当成熟,我们从这里开始研究第二种方法,探究新的傅里叶变换的定义。
傅里叶变换的最佳函数
首先找出最适合进行傅里叶变换的函数,这类函数被称为\( S\)(Schwartz定义了这类函数,洛朗·施瓦茨,法国数学家)。\( S\)需要满足两个前提条件:
1. 如果\( f(t) \in S\),那么\( \mathcal{F} f \in S\)
2. 如果\( f(t) \in S\),\( f(t)\)能进行傅里叶正逆变换的积分计算
\( \mathcal{F F}^{-1} f=f, \mathcal{F}^{-1} \mathcal{F} f=f\)
条件\( 1\)排除了\( \Pi\)函数,因为其傅里叶变换\( \operatorname{sinc}\)无法通过积分还原回去。条件\( 2\)排除了正余弦以及常数函数,因为它们的傅里叶变换没有被定义,无法执行积分运算。
速降函数(Rapidly Decreasing Functions)
\( S\)(Schwartz)作为最适合进行傅里叶变换的函数,也被叫作“速降函数”,设有速降函数\(f(x) \in S \)它的定义如下:
1. \( f(x)\)是无限可微的(光滑函数)
2. 对于任何\(m, n \geqslant 0 \),都有$$ \lim _{x \rightarrow \pm \infty}|x|^{n}\left|\frac{\partial^{m}}{\partial x^{m}} f(x)\right|=0 $$
即\( f(x)\)的任意阶导趋于\( 0\)的速度都比\( x\)的任意次方上升速度快。这些定义是由傅里叶的导数定理(derivative theorem)引申出来的。举个例子,比如函数\( f(x)=e^{-\pi x^{2}} \)。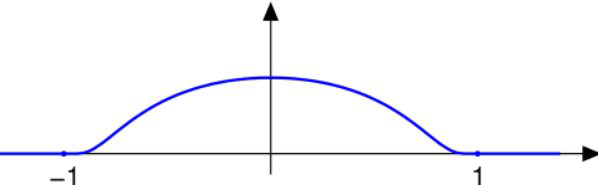
除了上面的高斯函数,还有一类函数,称为\( C\)(compact support)【紧支集函数】也属于速降函数,它满足:
(1) \( f(x)\)无穷可微
(2) \( f(x) \)仅在一个有限的区间内不为零
用最通俗的话来说,compact support是这样的,对于函数\(f(x)\),如果自变量\(x\)在\(0\)附近的取值范围内,\(f(x)\)能取到值,而在此之外,\(f(x)\)的取值为\(0\),那么这个函数\(f(x)\)就是禁支撑函数,而这个\(0\)附近的取值范围就叫作【紧支撑集】,比如在\([-1,1]\)之间的高斯函数。
“速降”的概念本质上来源于导数定理(下面的不太懂):$$\mathcal{F} f^{(n)}(s)=(2 \pi i s)^{n} \mathcal{F} f(s)$$
注:
(1) 这里将函数的光滑性由\( s\)的幂次来反映;或者说,这个式子展示了可微分性和衰减速率之间的关系;导数定理,解释了光滑程度和可微性和衰减速率之间的关系。
(2) 这个式子和微分方程之间有重大联系,并且产生了许多应用。在Heaviside的著作中,他引入了德尔塔函数用于求解微分方程,他采用变换的方式求解微分方程,用了很多变换,将微分运算变成乘法运算。
Parseval定理
$$\int_{-\infty}^{\infty}|\mathcal{F} f(s)|^{2} d s=\int_{-\infty}^{\infty}|f(x)|^{2} d x$$该等式表明信号在时域与频域的能量(功率)相等。其一般形式为:
设有\( f(x), g(x) \in S\),则$$\int_{-\infty}^{\infty} \mathcal{F} f(s)\overline{ \mathcal{F}g(s) } d s=\int_{-\infty}^{\infty} f(x) \overline{ g(x)} d x$$
推导如下:待续
注:
1. 维基百科对于Parseval's theorem的描述,在物理和工程上,Parseval's theorem通常写作$$\int_{-\infty}^{\infty}|x(t)|^{2} \mathrm{d} t=\frac{1}{2 \pi} \int_{-\infty}^{\infty}|X(\omega)|^{2} \mathrm{d} \omega=\int_{-\infty}^{\infty}|X(2 \pi f)|^{2} \mathrm{d} f$$The interpretation of this form of the theorem is that the total energy of a signal can be caluculated by summing power-per-sample across time or spectral power across frequency.
2. 知乎:帕塞瓦尔定理怎么证明?