时延性，尺度变化，卷积

时域函数和频域函数的对应关系$$f(t) \leftrightarrow F(s)$$

时延性(Delayed)$$f(t-b) \leftrightarrow ?$$关于时延性我们可以回忆一下波动方程\(  y=f\left(t-\displaystyle\frac{x}{v}\right)\)振动沿着正轴方向传播，这里的\(-\displaystyle\frac{x}{v} \)就是考虑处在\(  x\)处质点的振动相对于振动源的时延性。针对我们的\(  f(t-b)\)延后了\( b \)，那么在频域上如何变化呢？$$\begin{aligned} & \int_{-\infty}^{\infty} e^{-2 \pi i s t} f(t-b) d t \\ =& \int_{-\infty}^{\infty} e^{-2 \pi i s(u+b)} f(u) d u \quad u=t-b \\ =& \int_{-\infty}^{\infty} e^{-2 \pi i s u} e^{-2 \pi i s b} f(u) d u \\ =& e^{-2 \pi i s b} \int_{-\infty}^{\infty} e^{-2 \pi i s u} f(u) d u \\ =& e^{-2 \pi i s b} F(s) \end{aligned}$$因此$$\begin{array}{l} f(t-b) \leftrightarrow e^{-2 \pi i s b} F(s) \\ f(t \pm b) \leftrightarrow e^{\pm 2 \pi i s b} F(s) \end{array}$$时域上的时移对应频域上的相移，令$$F(s)=|F(s)| e^{2 \pi i \theta(s)}$$其中\(  |F(s)|\)表示振幅，即我们画的频域图的竖线长度，\( \theta(s) \)表示相位。那么$$e^{-2 \pi i s b} F(s)=|F(s)| e^{2 \pi i(\theta(s)-s b)}$$上面的等式代表了频谱的振幅不变，而相位改变了，或者说我们看到的二维频域图(不反映相位)在延迟前后没有任何变化，变化的相位部分不在图中展现出来，当然三维图可以画出来，即频率-系数实部-系数虚部，或者频率-系数模长-相位。

尺度变化(scaling)$$f(a t) \leftrightarrow ?$$当\(  a>0\)时$$\begin{aligned} & \int_{-\infty}^{\infty} e^{-2 \pi i s t} f(a t) d t \\ =& \int_{-\infty}^{\infty} e^{-2 \pi i s\left(\frac{u}{a}\right)} f(u) d \frac{u}{a} \quad u=a t \\ =& \frac{1}{a} \int_{-\infty}^{\infty} e^{-2 \pi i\left(\frac{s}{a}\right) u} f(u) d u \\ =& \frac{1}{a} F\left(\frac{s}{a}\right) \end{aligned}$$同样可以求当\( a<0 \)时$$\begin{aligned} & \int_{-\infty}^{\infty} e^{-2 \pi i s t} f(a t) d t \\ =& \int_{-\infty}^{\infty} e^{-2 \pi i s\left(\frac{u}{a}\right)} f(u) d \frac{u}{a} \quad u=a t \\ =& \frac{1}{a} \int_{\infty}^{-\infty} e^{-2 \pi i\left(\frac{s}{a}\right) u} f(u) d u \\ =&-\frac{1}{a} \int_{-\infty}^{\infty} e^{-2 \pi i\left(\frac{s}{a}\right) u} f(u) d u \\ =&-\frac{1}{a} F\left(\frac{s}{a}\right) \end{aligned}$$合并一下$$f(a t) \leftrightarrow \frac{1}{|a|} F\left(\frac{s}{a}\right)$$以高斯函数为例，展示尺度变化对信号的影响。

1. 当\(  a>1\)时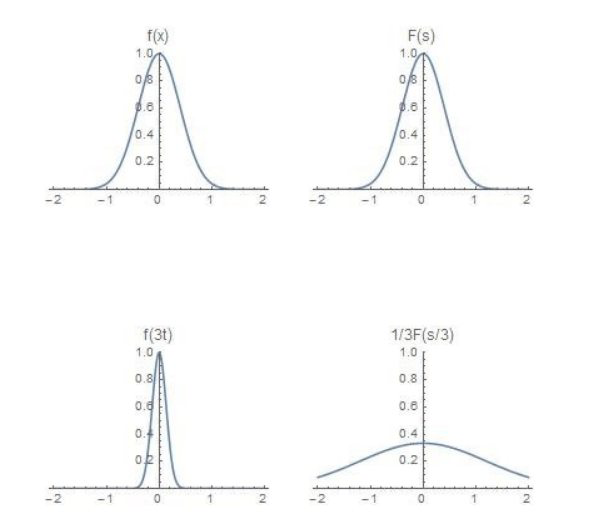

时域横向压缩，频域横向扩展、纵向压缩，即频域分散。

2. 当\( 0<a<1\)时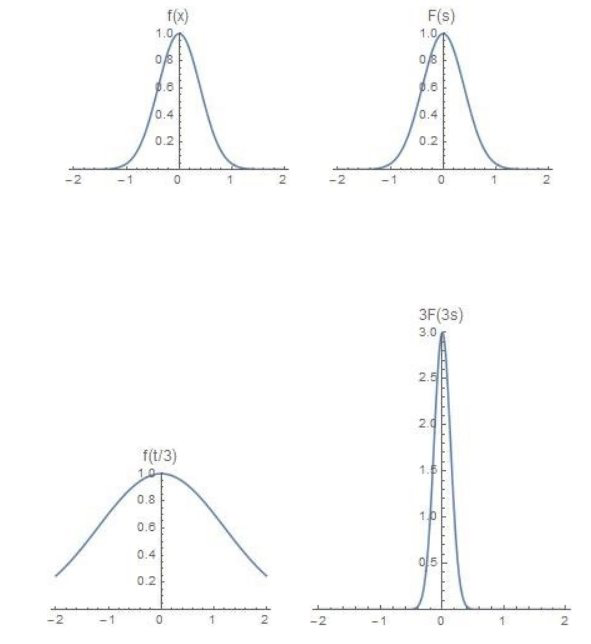

时域横向扩展，频域横向压缩、纵向扩展，即频域集中

上述情况表面了时域与频域不可能同时在一个方向上压缩与扩展(Signal cannot be both  localized in time and in frequency.)。在一个域上展宽，必然在另一个域压缩，反过来同样成立。还有其他方法得出这种关系，把这种关系变为精确的数学术语，其中最著名的要数海森堡测不准原理(不能同时确定粒子的位置和动量)，可以通过傅里叶变换来证明这个测不准原理。

高斯函数的傅里叶变换是其自身，you might say the Gaussian is perfectly balanced somehow in both time and frequency。

卷积(convolution)

信号处理最重要的operation：卷积。信号处理可以被理解为：如何用一个函数(信号)调制另一个函数(信号)。(Signal Processing can be said to how can you use one function(signal) to modify another.)

频谱操作更容易：大部分情况下，信号处理是着力于改变信号的频谱，也就是说，先对信号进行傅里叶变换，然后在频域进行处理，之后进行傅里叶逆变换得到处理过后的信号。时域中的卷积，频域中的乘法。

线性处理：即两个信号线性叠加$$\begin{aligned} \mathcal{F}(f+g) &=\int_{-\infty}^{\infty} e^{-2 \pi i s t}(f(t)+g(t)) d t \\ &=\int_{-\infty}^{\infty}\left(e^{-2 \pi i s t} f(t)+e^{-2 \pi i s t} g(t)\right) d t \\ &=\int_{-\infty}^{\infty} e^{-2 \pi i s t} f(t) d t+\int_{-\infty}^{\infty} e^{-2 \pi i s t} g(t) d t \\ &=\mathcal{F} f+\mathcal{F} g \end{aligned}$$

注：傅里叶变换的线性性质(\( \mathcal{F} \)是一个线性算符)
若函数\(  f(x)\)和\( g(x) \)的傅里叶变换\(  \mathcal{F}[f]\)和\(  \mathcal{F}[g]\)都存在，\(\alpha   \)和\( \beta \)为任意常系数，则\( \mathcal{F}[\alpha f+\beta g]=\alpha \mathcal{F}[f]+\beta \mathcal{F}[g] \)。

频域相乘处理$$\begin{aligned} \mathcal{F}(f) \mathcal{F}(g) &=\int_{-\infty}^{\infty} e^{-2 \pi i s t} g(t) d t \int_{-\infty}^{\infty} e^{-2 \pi i s x} g(x) d x \\ &=\iint_{-\infty}^{\infty} e^{-2 \pi i s t} e^{-2 \pi i s x} g(t) f(x) d t d x \\ &=\iint_{-\infty}^{\infty} e^{-2 \pi i s(t+x)} g(t) f(x) d t d x \\ &=\int_{-\infty}^{\infty}\left(\int_{-\infty}^{\infty} e^{-2 \pi i s(t+x)} g(t) d t\right) f(x) d x \\ &=\int_{-\infty}^{\infty}\left(\int_{-\infty}^{\infty} e^{-2 \pi i s(u)} g(u-x) d u\right) f(x) d x \quad u=t+x \\ &=\int_{-\infty}^{\infty}\left(\int_{-\infty}^{\infty} g(u-x) f(x) d x\right) e^{-2 \pi i s u} d u \end{aligned}$$令\(  h(u)=\int_{-\infty}^{\infty} g(u-x) f(x) d x\)因此$$(\mathcal{F} g)(\mathcal{F} f)=\int_{-\infty}^{\infty} e^{-2 \pi i s u} h(u) d u$$卷积定义

用符号\(  *\)表示，运算方法如下$$\begin{array}{c} (g * f)(x)=\displaystyle\int_{-\infty}^{\infty} g(x-y) f(y) d y \\ \mathcal{F}(g * f)=(\mathcal{F} g)(\mathcal{F} f) \end{array}$$信号的卷积的傅里叶变换等于对这些信号进行傅里叶变换后的乘积。

注：这里\(  (\mathcal{F} g)(\mathcal{F} f)\)严格来说中间应该用一个点乘，两个函数点乘是一个point-wise multiplication: (参考知乎)\( \left\{v_{1}, v_{2}, v_{3}\right\}^{T} \odot\left\{w_{1}, w_{2}, w_{3}\right\}^{T}=\left\{v_{1} w_{1}, v_{2} w_{2}, v_{3} w_{3}\right\}^{T} \)

卷积的代数性质：

• Commutativity, \(f * g=g * f\)
• Associativity, \(f *(g * h)=(f * g) * h\)
• Distributivity, \(f *(g+h)=(f * g)+(f * h)\)
• Associativity with scalar multiplication, \(a(f * g)=(a f) * g\)
• Inverse element, Some distributions \(S\) have an inverse element \(S^{-1}\) for the convolution\(S^{-1} * S=\delta\) The set of invertible distributions forms an abelian group under the convolution.
• Complex conjugation, \(\overline{f * g}=\bar{f} * \bar{g}\)
• Relationship with differentiation, \((f * g)^{\prime}=f^{\prime} * g=f * g^{\prime}\)
• 等等，参考wiki 以及史上最全的卷积性质及其证明—知乎