麦克斯韦方程组的边界条件

麦克斯韦方程组在不同介质的边界处，“自带”边界条件，可以通过积分形式处理。

对于\( \nabla \cdot \vec{D}=\rho_{f} \)，我们改写成$$\displaystyle\oint \vec{D} \cdot d \vec{S}=\displaystyle\int \rho_{f} d \tau$$

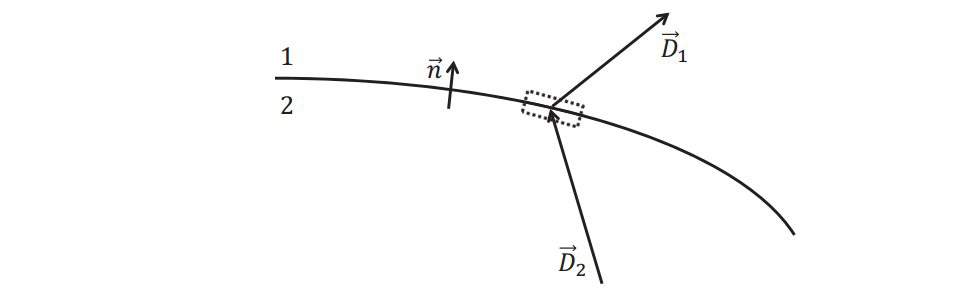
按图中方法，定义了截面的单位矢量方向。我们取虚线部分的扁平柱体(高度为\(  h\))，对于柱体的上下两个薄面来说有\(  \Delta \vec{S}_{1}=\Delta S \vec{n}\)和\(  \Delta \vec{S}_{2}=-\Delta S \vec{n}\)。我们不能取数学意义上的无线扁平，但是可以选择物理意义上的扁平(厚度10 nm左右，可以包裹界面电荷)，对此，我们依旧可以认为该柱体四侧面积接近零，于是对整个柱体进行电位移矢量的面积分有$$\displaystyle\oint \vec{D} \cdot d \vec{S}=\Delta \vec{S}_{1} \cdot \vec{D}_{1}+\Delta \vec{S}_{2} \cdot \vec{D}_{2}=\Delta S \cdot\left(\vec{n} \cdot \vec{D}_{1}-\vec{n} \cdot \vec{D}_{2}\right)=q_{f}$$等式右边表示的是柱体内的自由电荷量(不包含极化产生的束缚电荷，因为原始的公式等式左侧就是对源电荷的响应)，当上下两侧面积趋近于零，我们可以得到(历史上最先确定的公式)$$\vec{n}_{1} \cdot\left(\vec{D}_{1}-\vec{D}_{2}\right)=\sigma_{f}$$即\( \sigma_{f}=q_{f} / \Delta S \)是交界面上的自由电荷面密度。在一般情况下\(  \sigma_{f}=0\)，比如如果是体分布，那么取无限薄面，显然电荷密度为零，或者直接是没有自由电荷的情况。由于界面上电荷的面分布往往是均匀电荷密度的，因此\( \vec{n}_{1} \cdot\left(\vec{D}_{1}-\vec{D}_{2}\right) \)是一个常数，即有界面上任何地方来说，两侧电位移矢量的差值(或者说电位移矢量变化量，这里是一个突变)在法线方向的投影守恒，讲义上写的是\(  D\)场法向分量守恒。 D场已经抛去了极化电荷，只看得见自由电荷。

同理对于方程\(\nabla \cdot \vec{B}=0  \)，容易得到\( B \)场的法向分量连续的结论（？？？？？）：$$\vec{n} \cdot\left(\vec{B}_{1}-\vec{B}_{2}\right)=0 \Rightarrow B_{n 1}=B_{n 2}$$

第四条方程\(\nabla \times \vec{H}=\vec{j}_{f}+\displaystyle\frac{\partial \vec{D}}{\partial t}  \) 的积分形式   $$\displaystyle\oint \vec{H} \cdot d \vec{l}=\displaystyle\int_{S} \vec{j}_{f} \cdot d \vec{S}+\displaystyle\int \displaystyle\frac{\partial}{\partial t} \vec{D} \cdot d \vec{S}$$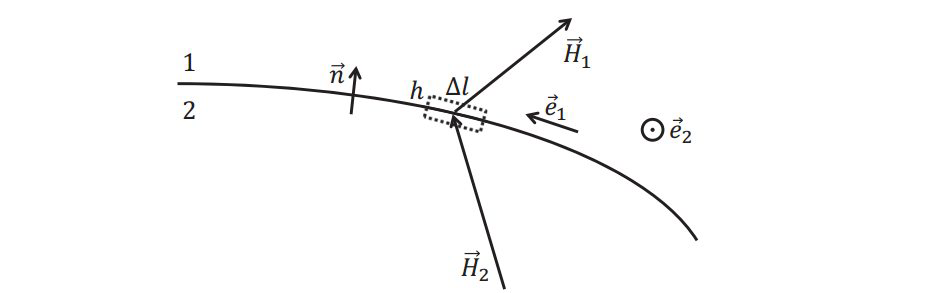假设\(   \vec{e}_{1}, \vec{e}_{2}\)为界面上相互垂直的两个方向矢量，其与截面方向矢量\(\vec{n}  \)呈右手螺旋：$$\vec{n} \times \vec{e}_{1}=\vec{e}_{2} \quad \vec{n} \times \vec{e}_{2}=-\vec{e}_{1}$$不考虑厚度，同样沿着环路积分有$$\begin{aligned} \vec{H}_{1} \cdot \Delta \vec{l}_{1}+\vec{H}_{2} \cdot \Delta \vec{l}_{2} &=\displaystyle\oint \vec{H} \cdot d \vec{l} \\ &=\displaystyle\int\left(\vec{j}_{f}+\displaystyle\frac{\partial \vec{D}}{\partial t}\right) \cdot d \vec{S} \\ &=\vec{j}_{f} \cdot \vec{e}_{2}(h \cdot \Delta l)+\displaystyle\frac{\partial}{\partial t}(D \cdot \Delta l \cdot h) \end{aligned}$$

继续补充