介质中的麦克斯韦方程组

介质的极化及磁化

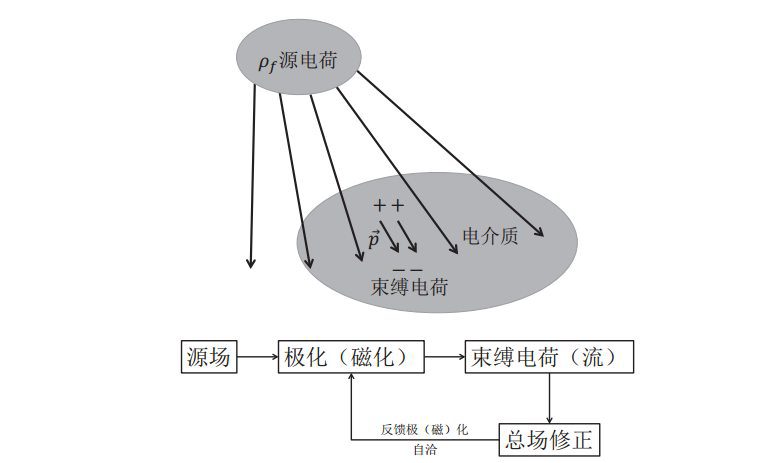
电磁场的最终来源是电荷及电流，只要空间某处存在某种电荷/电流(无论其起源)，就有电磁场产生，而与那个地方有无物质/什么物质无关！

介质在电场作用下，产生电偶极子，在磁场作用下，产生磁偶极子。即产生了束缚于电(磁)介质的极化电荷/磁化电流，它们与源场的电荷/电流一起，共同组成了总场(总场是介质即使最终感受到的场)。个人感觉有点类似PID控制。

电介质感受到电场之后，正负电荷被拉开，形成电偶极子；无磁性磁介质感受到磁场后，形成分子环流(磁偶极子)，这就是“磁化”过程。

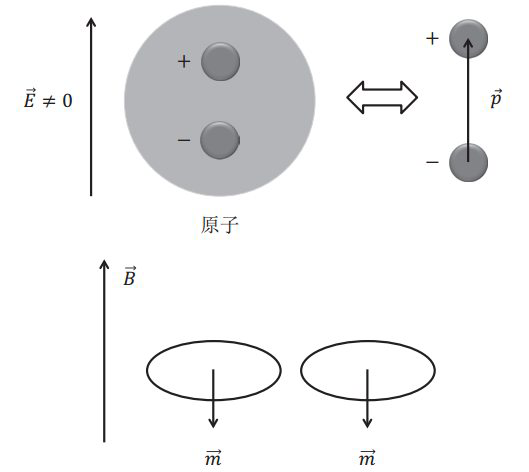
极化和磁化的过程还有另外的可能性。体系中的构成单元原本就是带有固有电(磁)偶极矩的，但是由于热运动作用，这些电(磁)偶极矩都是随机排列的，总体宏观不表现出极性/磁性；但是加上外界电(磁)场，电(磁)偶极矩出现了宏观表现上的定向排列，因此产生了宏观电(磁)矩。为了描述极化(磁化)的大小，定义【极化(磁化)强度】的两个宏观量，其定义为单位体积内分子电(磁)偶极矩的矢量和)$$\vec{P}=\displaystyle\frac{\sum_{i} \vec{p}_{i}}{\Delta V} \quad \vec{M}=\displaystyle\frac{\sum_{i} \vec{m}_{i}}{\Delta V}$$上面的宏观量，既要考虑每一个微观电(磁)偶极子的大小，又要考虑分布密度。在低场近似下，很多材料对电磁场线性响应(一阶近似)，即$$\vec{P}(\vec{r}, t)=\varepsilon_{0} \chi_{e} \vec{E}(\vec{r}, t) \quad \vec{M}(\vec{r}, t)=\displaystyle\frac{1}{\mu_{0}} \displaystyle\frac{\chi_{m}}{1+\chi_{m}} \vec{B}(\vec{r}, t)$$

上面的电场和磁场是介质分子感受到的局域总场(不仅是源场)，\(  \chi_{e}\)为【极化率】，\(  \chi_{m}\)为【磁化率】，它们形象理解就是在电(磁)场作用下，它们数值如果大的话，表示介质越听电(磁)场的话，介质分子比较团结一致，指哪里打哪里。

注：
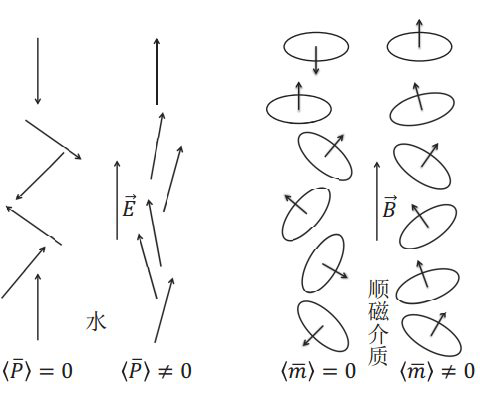
(1)回顾什么是顺磁性材料，来自MIT-电和磁，顺磁性物质，在没有外界磁场下，每一个微元“磁矩”都是随机排列的，宏观上表现出没有方向性，随着外界磁场越来越强，宏观表现出的方向性越来越强，也就是说，单个“磁矩”来看，它们产生的磁场方向似乎是随机的（热运动导致的），但是宏观统计上表现出一定的方向性。外界磁场移去后，立马不存在宏观上的方向性，恢复到初始的杂乱无章的状态。
(2)  原子中的电子有自旋偶极矩(洪特法则)；
(3)  用大写的\(\vec{P}  \)/\( \vec{M} \)表示宏观的极化(磁化)强度，而小写的\( \vec{p}_{i} \)/\( \vec{m}_{i} \)表示微观的电(磁)偶极子的电(磁)矩。

 

极(磁)化电荷(流)

极化电荷

【极化电荷】： 由于极化，正负电荷间发生了相对位移，每处的正负电荷 可能不完全抵消，这样就呈现出束缚在介质中的宏观电荷，称为极化电荷。假设空间的极化强度分布为\(\vec{P}(\vec{r})  \)，我们在\(  \vec{r}\)点附近取一块宏观小微观大的区域\( \tau \)，其边界由\( \vec{S} \)给定，计算这中间包含的极化总电荷\(Q_{P} \)。现在只需考虑“插”在边界上的偶极子，它们才对\(  Q_{P}\)有贡献。

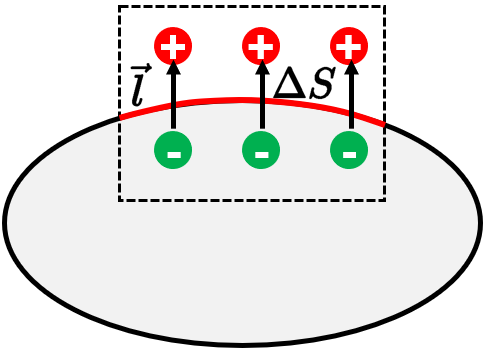设偶极子数密度为\( n \)，每个偶极子一端的带电量为\(  q\)，那么在\(  \)体积内，这些偶极子对区域内的净电荷数为\(d Q_{P}=-q n \vec{l} \cdot d \vec{S}=-\vec{P} \cdot d \vec{S}  \)，考虑所有穿过截面的偶极子的贡献，那么区域\( \tau \)内的总的束缚电荷为$$Q_{P}=-\displaystyle\oint_{S} \vec{P} \cdot d \vec{S}$$运用高斯定理，容易得到【极化电荷密度】$$\rho_{P}=-\nabla \cdot \vec{P}$$注：如果对一个均匀极化的介质，就不存在极化强度\(\vec{P}  \)的源了，即散度为零，根据上面公式，极化电荷密度为零，显然有问题。上式成立的关键是“宏观很小微观很大”，宏观很小，简单来说就是我们能测量的尺度上的大小，微观很大是相对于电偶极子的分布来说的，这个区域可以包含很多很多电偶极子，该处这些偶极子的统计宏观表现(平均化)就是该处的极化强度，这是电动力学处理宏观连续介质的精髓，整个物体就表现出极化强度宏观上的连续性。类比一下，量子力学中，如果相邻能级之间的能量差很小很小，那么我们同样可以把它们当做“连续的能带”处理。

【极化电流】：前面有\( \rho_{P}=-\nabla \cdot \vec{P} \)，如果\( \vec{P} \)随时间变化，那么束缚电荷密度\(  \rho_{P}\)也会随时间变化，于是产生极化电流。

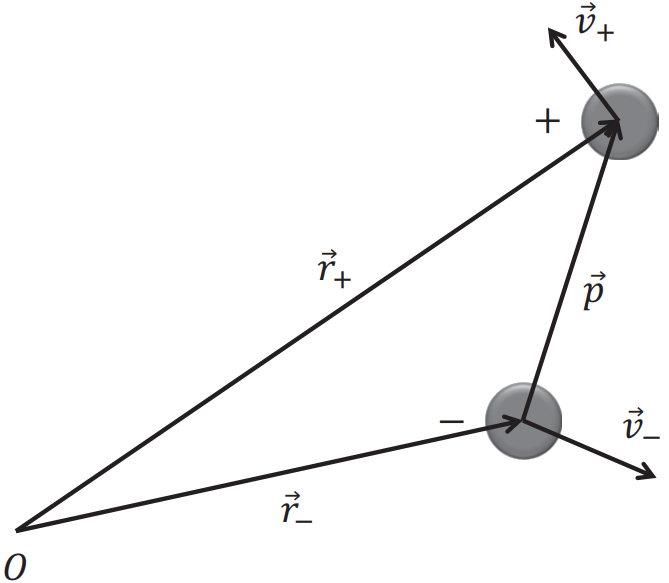
考虑单位体积内一个电偶极子，运动引起的极化电流密度为$$\vec{j}_{P}(\vec{r})=\rho_{+} \vec{v}_{+}+\rho_{-} \vec{v}_{-}=\displaystyle\frac{\partial}{\partial t}\left(\rho_{+} \vec{r}_{+}+\rho_{-} \vec{r}_{-}\right)$$而该处的极化强度为$$\vec{P}=\displaystyle\frac{\vec{p}}{\Delta \Omega}=\displaystyle\frac{q\left(\vec{r}_{+}-\vec{r}_{-}\right)}{\Delta \Omega}=\rho_{+} \vec{r}_{+}+\rho_{-} \vec{r}_{-}$$所以极化电流密度$$\vec{j}_{P}=\displaystyle\frac{\partial \vec{P}}{\partial t}$$ 据叠加原理，上式在有许多偶极子存在时依然正确 。检验是否满足流守恒定律$$\nabla \cdot \vec{j}_{P}+\displaystyle\frac{\partial \rho_{P}}{\partial t}=\nabla \cdot \displaystyle\frac{\partial \vec{P}}{\partial t}-\displaystyle\frac{\partial}{\partial t} \nabla \cdot \vec{P} \equiv 0$$完美！物质极化以后，产生的极化强度有两个效应，一个是产生极化电荷密度，二是极化电荷运动(极化电荷密度随时间变化)会产生极化电流密度，因此满足流守恒。

磁化电流

磁化强度，对应于大量的磁偶极子，磁偶极子究其本质都是分子环流，那么宏观上到底给我们多少附加的束缚电流？这个电流和之前讨论的极化电流，究其本质都是一样的，不能脱离介质而存在，一定是束缚在介质上的，所以也叫束缚电流。

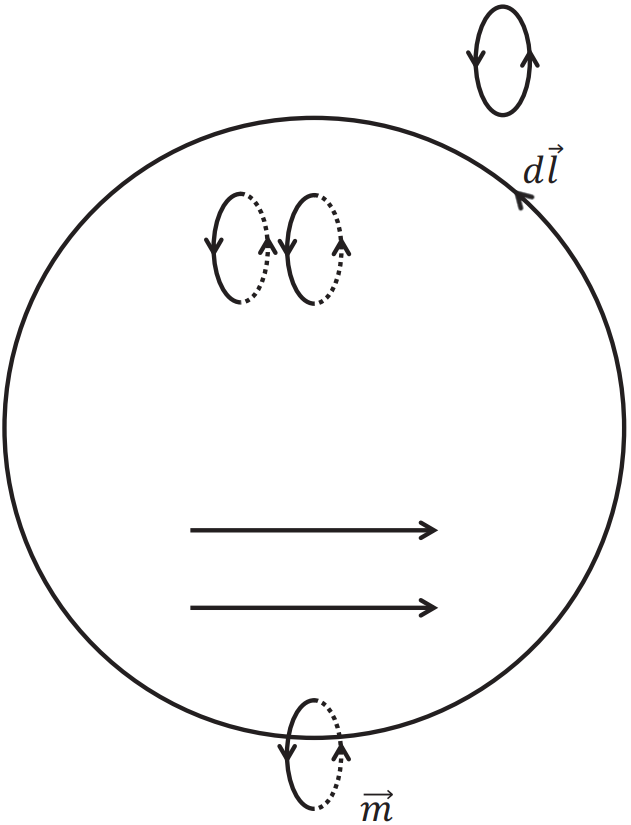这一圈里面，到底因为磁化，产生了多少磁化电荷？或者说挂上了多少分子环流(类比钥匙环)？只计算那些与边界铰链的环流，因为它们只对\( S \)面内贡献一次电流。考虑一段边界\(  d \vec{l}\)铰链的分子环流，设每个分子环流的电流为\(  i\)，线圈面积为\( \Delta \vec{s} \)，显然在\( \Delta \vec{s} \cdot d \vec{l} \)体积内所有的磁偶极子都对\(  S\)内的净电流有贡献，假设偶极子的体密度为\( n \)，则\(  d \vec{l}\)边界对\( I_{M} \)的贡献为$$d I_{M}=i \times n \Delta \vec{s} \cdot d \vec{l}=\vec{M} \cdot d \vec{l}$$环路积分一下【磁化电流】$$I_{M}=\displaystyle\oint \vec{M} \cdot d \vec{l}$$这就是宏观小微观大的区域里面，由于磁化强度而产生的磁化电流大小。等式左边\( I_{M}=\displaystyle\int \vec{j}_{m} \cdot d \vec{S} \)，等式右边斯托克斯定理\( \displaystyle\oint \vec{M} \cdot d \vec{l}=\displaystyle\int \nabla \times \vec{M} \cdot d \vec{S} \)于是磁化电流密度$$\vec{j}_{m}=\nabla \times \vec{M}$$两边取散度得到\(\nabla \cdot \vec{j}_{m}=0  \)，根据流守恒\(  \displaystyle\frac{\partial \rho_{M}}{\partial t}=0\)磁化电流不引起电荷的积累，因此不用考虑磁化电荷密度(从没有介质到有介质，都不改变这个公式，而没有介质的时候磁化电荷为零，因此有介质的时候还是零)。究其本质，还是没有磁荷(磁单极子)的表现，或者说分子环流本身是闭合的。

 

介质中的麦克斯韦方程组汇总

前面我们讨论了极(磁)化电流(荷)如何影响总的电(磁)场。当介质存在时，空间电荷包含源场的电荷以及极化电荷(束缚电荷)，没有磁化导致的束缚电荷，因此总的电荷\( \rho_{t} \)表示为$$\rho_{t}=\rho_{f}+\rho_{P}=\rho-\nabla \cdot \vec{P}$$介质中可能的电流有传导电流(来自源场)、极化电流和磁化电流，因此总电流为$$\vec{j}_{t}=\vec{j}_{f}+\displaystyle\frac{\partial \vec{P}}{\partial t}+\nabla \times \vec{M}$$在麦克斯韦方程组中，不管\(  \rho\)和\( \vec{j} \)的来源如何，只要是电荷或电流，它们都将在空间激发电场或磁场。所以介质中的麦克斯韦方程组修改为$$\left\{\begin{array}{l} \nabla \cdot \vec{E}=\displaystyle\frac{1}{\varepsilon_{0}}\left(\rho_{f}-\nabla \cdot \vec{P}\right) \\ \nabla \times \vec{E}=-\displaystyle\frac{\partial}{\partial t} \vec{B} \\ \nabla \cdot \vec{B}=0 \\ \nabla \times \vec{B}=\mu_{0} \varepsilon_{0} \displaystyle\frac{\partial}{\partial t} \vec{E}+\mu_{0}\left(\vec{j}_{f}+\displaystyle\frac{\partial \vec{P}}{\partial t}+\nabla \times \vec{M}\right) \end{array}\right.$$配合\(\vec{P}(\vec{r}, t)=\varepsilon_{0} \chi_{e} \vec{E}(\vec{r}, t) \quad \vec{M}(\vec{r}, t)=\displaystyle\frac{1}{\mu_{0}} \displaystyle\frac{\chi_{m}}{1+\chi_{m}} \vec{B}(\vec{r}, t)  \)整个方程组才可解，当然前提是要知道介质对外场的响应的相关系数。上面麦克斯韦方程组，等式右边既包含源场(输入)，又包含响应(磁/极化后产生的新场)，物理图像不清晰。回忆我们在学习微分方程的时候，都是把输入(源)写在等式的右边，等式左边就是对应的响应，即“拉普拉斯变换”的思想，这里我们也采用类似的方法。引入两个辅助矢量【电位移矢量】(Electric displacement field)和所谓的"磁场强度"矢量$$\vec{D}=\varepsilon_{0} \vec{E}+\vec{P} \quad \quad\quad \vec{H}=\displaystyle\frac{\vec{B}}{\mu_{0}}-\vec{M}$$于是介质中的麦克斯韦方程组可以写为(源场都放在右边)$$\left\{\begin{array}{l} \nabla \cdot \vec{D}=\rho_{f} \\ \nabla \times \vec{E}=-\displaystyle\frac{\partial}{\partial t} \vec{B} \\ \nabla \cdot \vec{B}=0 \\ \nabla \times \vec{H}-\displaystyle\frac{\partial \vec{D}}{\partial t} =\vec{j}_{f}\end{array}\right.$$两个辅助矢量的引入使方程组只出现自由电荷和自由电流，仅仅是为了(数学上)讨论方便，它们本身不是真实的场，它们不会对身处其中的电荷/电流产生作用力。

 

本构关系

这堂课，精彩！

这里讨论的是修正之后的局域总场是如何与极(磁)化程度自恰的。我们需要确定新引入的矢量\( \vec{D} \)、\( \vec{H} \)与\(\vec{E}  \)、\(\vec{B}  \)之间的关系才能求出方程组的解。这些关系式就是本构关系，与具体的材料有关—材料性质千变万化，本构关系也各不相同。

我们讨论最简单的情况，就是线性介质的本构关系，我们有$$\left\{\begin{array}{l} \vec{D}=\varepsilon \vec{E} \\ \vec{H}=\vec{B} / \mu \end{array}\right.$$其中介电常数和磁导率可以写成$$\varepsilon=\varepsilon_{r} \varepsilon_{0}=\left(1+\chi_{e}\right) \varepsilon_{0} \quad \mu=\mu_{r} \mu_{0}=\left(1+\chi_{m}\right) \mu_{0}$$另外根据前面的\(  \vec{M}(\vec{r}, t)=\displaystyle\frac{1}{\mu_{0}} \displaystyle\frac{\chi_{m}}{1+\chi_{m}} \vec{B}(\vec{r}, t)\)结合\(  \mu=\mu_{r} \mu_{0}=\left(1+\chi_{m}\right) \mu_{0}\)以及\( \vec{H}=\vec{B} / \mu \)，可以得到$$\vec{M}=\chi_{m} \vec{H}  $$这个式子才是和\( \vec{P}(\vec{r}, t)=\varepsilon_{0} \chi_{e} \vec{E}(\vec{r}, t) \)对称的，但是历史的错误导致人们以为\( \vec{H} \)是基本量，命名为磁场强度，与\(\vec{E}  \)的地位对应，但是实际上本质的物理量是\( \vec{B} \)(磁感应强度，名字都被抢走了，气炸)。用本构关系再次改写介质中无源的麦克斯韦方程组得到$$\left\{\begin{array}{l} \nabla \cdot \vec{E}=0 \\ \nabla \times \vec{E}=-\mu \displaystyle\frac{\partial \vec{H}}{\partial t} \\ \nabla \cdot \vec{H}=0 \\ \nabla \times \vec{H}=\varepsilon \displaystyle\frac{\partial \vec{E}}{\partial t} \end{array}\right.$$其中\(  \vec{E}\)和\(\vec{H}  \)完美对称，另外需要指出的是：导体本身就是一种特殊的电磁介质，它的本构关系就是欧姆定律\(\vec{j}=\sigma \vec{E}  \)。

我们上面讨论的都是最简单也最常见的线性响应对应的本构关系，更一般的情况，响应各种各样，丰富多彩：
(1)  各向异性介质，介电常数和磁导率都是对称张量；
(2)  铁电/铁磁性物质，或者强场作用，不能忽略高阶项，那么需要考虑非线性效应，\(\vec{P}  \)与\(\vec{E}  \)、\( \vec{M} \)与\( \vec{H} \)不再是线性响应；
(3)  高频情况，比较复杂；
(4)  局域效应，比较复杂；
(5)  相对介电常数\(\varepsilon_{r}=1+\chi_{e}  \)，相对磁导率\( \mu_{r}=1+\chi_{m} \)。