图像法和数值法

解函数的图像

前面我们介绍的都是可以解的一阶和二阶常微分方程，通常是常系数线性方程。但是有很多常微分方程，它的解函数存在，但是无法得到函数的解析式，这里我们主要讨论解函数的图像(Pictures of the Solutions)，而不是讨论如何求解解函数。

首先讨论一阶常微分方程\(\displaystyle\frac{d y}{d t}=f(t, y)  \)，那么我在二维平面上每取一个点，都可以按照类似向量场(Vector field)的方式来处理，然后用matlab绘制出来。

例子1 \(\displaystyle\frac{d y}{d t}=2-y  \)  平面上按一定间距选出一些点，然后根据给出的公式可以算出每一点的斜率，由于在矢量场中，每一个箭头既有大小又有方向，而我们这里只讨论方向，所以让每一点的向量为\( (1, y^\prime) \)，然后对向量的模长进行归一化，就得到图中的箭头。

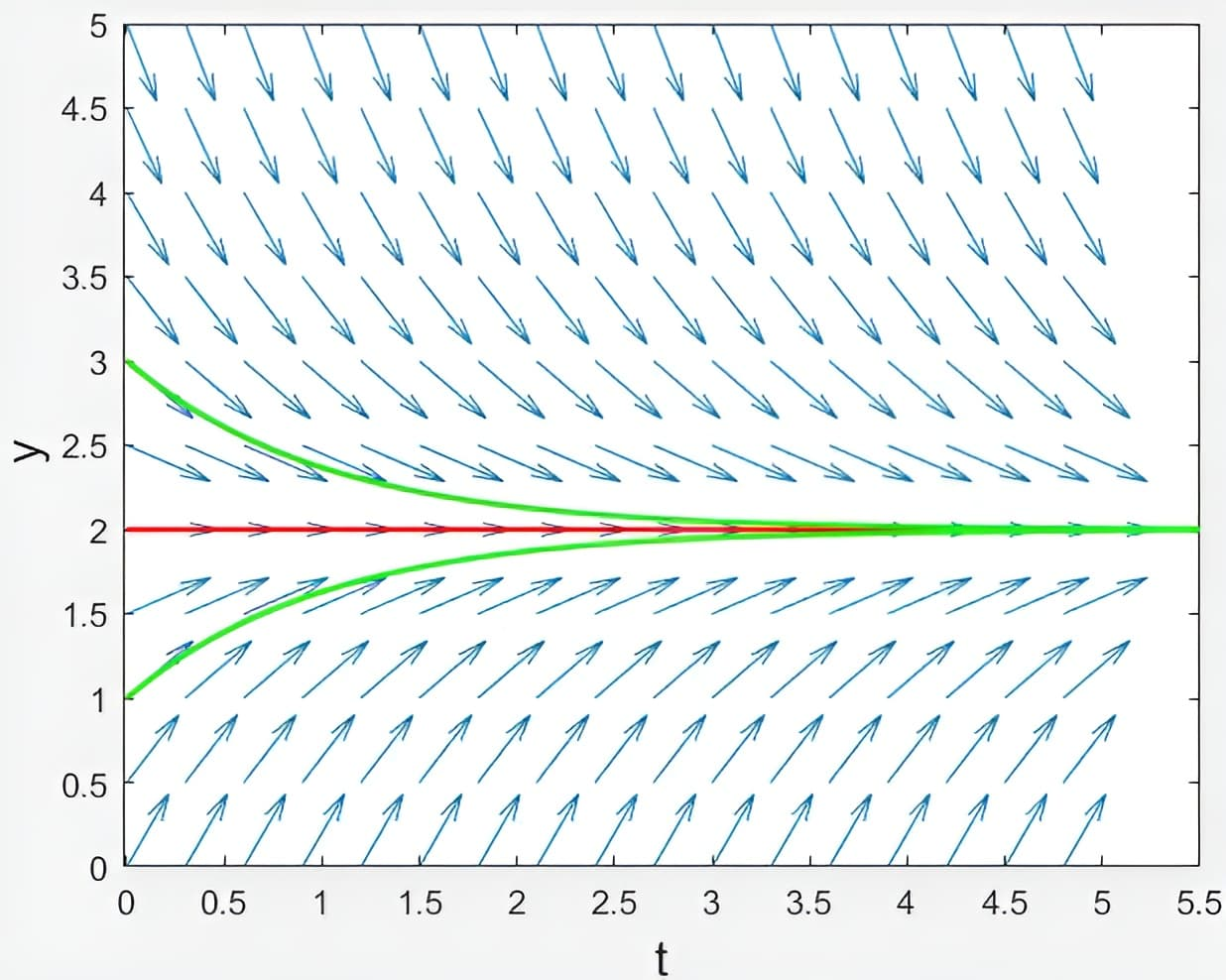
图的特点：
(1)  沿着\(  y=2\)的红线上，箭头的方向都是水平向右的，对应的函数的导数正好就是零，红线之上的箭头都指向下面，红线之上的箭头都指向上面；
(2) 从起始点开始，两条绿线都是随着时间的增加，越来越接近红线，红线成为两条绿线的渐近线，或者说两条绿线的函数值越来越接近\( 2 \)；
(3)  上下两条绿线的表达式分别为\(y(t)=2+ e^{-t}  \)和\( y(t)=2- e^{-t} \)，其实就是初始值决定了通式\(y(t)=2+C e^{-t}  \)中常系数的确定。

[x,y] = meshgrid(0:0.3:5,0:0.5:5);
uu=x-x+1;
vv=2-y;
u=uu./sqrt(uu.*uu+vv.*vv);
v=vv./sqrt(uu.*uu+vv.*vv);
quiver(x,y,u,v)
hold on
m=linspace(0,5.5);
n=m-m+2;
plot(m,n,'r','LineWidth',1.5)
hold on
q1=2+exp(-m);
q2=2-exp(-m);
plot(m,q1,'g','LineWidth',1.5)
plot(m,q2,'g','LineWidth',1.5)
axis([-0.02,5.5,0,5])
xlabel(' t ','fontsize',15)
ylabel('y ','fontsize',15)

例子2 \(\displaystyle\frac{d y}{d t}=y-y^{2} \) ，可以求得函数\( y(t)=\displaystyle\frac{1}{1+C e^{-t}} \)。从微分方程很容易确定函数的两个定点(fixed points)：\(  y=0\)和\(y=1  \)，两者都会让导数为\( 0 \)。

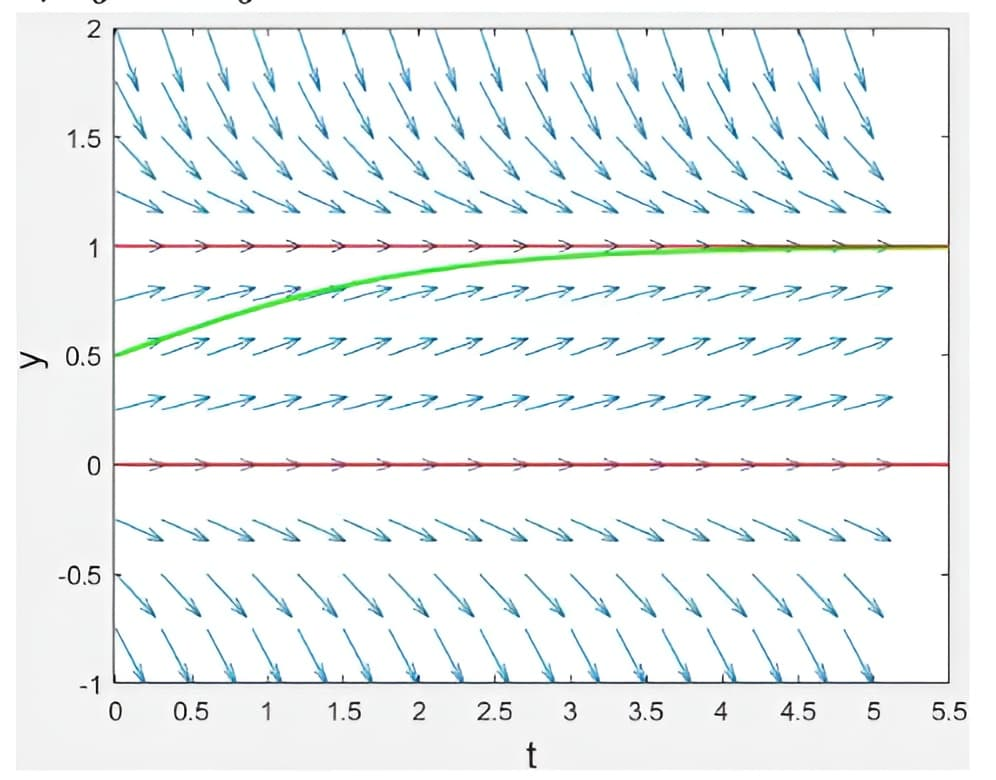
图中的绿线(\( C=1 \)的情况)就是S-curve的一部分，两条红线对应倒数为零的定点。

[x,y] = meshgrid(0:0.3:5,-1:0.25:2);
uu=x-x+1;
vv=y-y.*y;
u=uu./sqrt(uu.*uu+vv.*vv);
v=vv./sqrt(uu.*uu+vv.*vv);
quiver(x,y,u,v)
hold on
m=linspace(0,5.5);
n=1./(1+exp(-m));
plot(m,n,'g','LineWidth',1.5)
q1=m-m;
q2=m-m+1;
plot(m,q1,'r','LineWidth',1)
plot(m,q2,'r','LineWidth',1)
axis([-0.02,5.5,-1,2])
xlabel(' t ','fontsize',15)
ylabel('y ','fontsize',15)

例子3  \(\displaystyle\frac{d y}{d t}=1+t-y  \)，可以求得\(y(t)=t+C e^{-t}  \)
两条外侧红色平行线分别表示\( 1+t-y=0 \)和\( 1+t-y=2 \)，两个绿线分别表示\(y(t)=t+e^{-t}  \)和\( y(t)=t- e^{-t}  \)。红线是“等值线”，表示线上个点的导数值是相等的。中间的那条红线是\( 1+t-y=1 \)，即\(  y=t\)，是一条很特殊的直线，因为这也是“解曲线”，和两条绿线是一样的，都是方程的解之一，其实也是通式\( y(t)=t+C e^{-t}  \)中\( C=0 \)的情况。其他\( C\not=0 \)时，函数最终也是趋向于\(  y=t\)。

[x,y] = meshgrid(0:0.3:5,-4:1:6);
uu=x-x+1;
vv=1+x-y;
u=uu./sqrt(uu.*uu+vv.*vv);
v=vv./sqrt(uu.*uu+vv.*vv);
quiver(x,y,u,v)
hold on
m=linspace(0,5.5);
n1=m+exp(-m);
n2=m-exp(-m);
plot(m,n1,'g','LineWidth',1.5)
plot(m,n2,'g','LineWidth',1.5)
q1=m+1;
q2=m-1;
q3=m;
plot(m,q1,'r','LineWidth',1)
plot(m,q2,'r','LineWidth',1)
plot(m,q3,'r','LineWidth',1)
axis([-0.02,5.5,-4,6])
xlabel(' t ','fontsize',15)
ylabel('y ','fontsize',15)

 

相平面

源、汇和鞍

本讲还是在讨论微分方程的图像，但是是关于二阶常系数线性常微分方程，主要讨论齐次，其解函数为\(  y=c_{1} e^{s_{1} t}+c_{2} e^{s_{2} t}\)，解函数的导数为\(y^{\prime}=c_{1} s_{1} e^{s_{1} t}+c_{2} s_{2} e^{s_{2} t}  \)。【相平面】(Phase Plane Pictures)的横纵坐标分别是\( y \)和\( y^{\prime} \)。

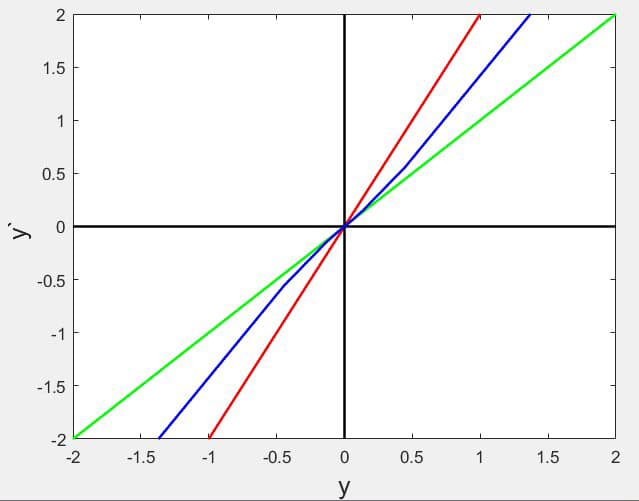
例子1    \(  y^{\prime \prime}-3 y^{\prime}+2 y=0\)
注意一阶导数即阻尼项系数为负数，所以解函数为不稳定函数最终会趋于无穷。从特征方程\(s^{2}-3 s+2=0  \)可以得到\(s_{1}=1, s_{2}=2  \)。因此有\(y=c_{1} e^{t}+c_{2} e^{2 t}, \quad y^{\prime}=c_{1} e^{t}+c_{2} 2 e^{2 t}  \)。

(1) 当\( c_{1}=\pm 1, c_{2}=0 \)时，\( y=e^{t} , y^{\prime}=e^{t} \)或者\( y=-e^{t} , y^{\prime}=-e^{t}  \)，分别对应于直线\( y^{\prime}=y \)在第一象限和第三象限的部分，对应的是绿线。

(2) 当\( c_{1}=0, c_{2}=\pm 1 \)时，\( y=e^{2t} , y^{\prime}=2e^{2t} \)或者\( y=-e^{2t} , y^{\prime}=-2e^{2t}  \)，分别对应于直线\( y^{\prime}=2y \)在第一象限和第三象限的部分，对应的是红线。

(3)  取\( c_{1}=1, c_{2}=1 \)，则有\( y=e^{t}+e^{2 t} \quad y^{\prime}=e^{t}+2 e^{2 t} \)，对应于图中的蓝线。在\(+0 \)附近，靠近绿线，最后斜率不断增加，平行于红线第一象限；在\(-0 \)附近，同样靠近绿线，最后斜率不断增加，平行于红线。也就是说\(  t\)从\( 0 \)出发，它的解接近于情形(1)，当\( t \)绝对值很大，它的解接近于情形(2)。
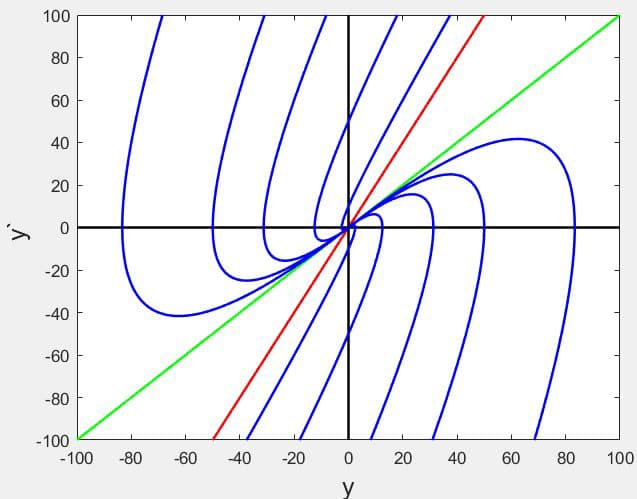
(4) 对于图上任意一点，一旦确定了，那么我们就可以根据二元二次方程组求出对应的\(c_{1}  \)和\(c_{2}  \)，就可以画出响应的图像。对于下部分的蓝色曲线，我们对应于\( c_{1}=1 \)，\( c_{2} =-0.02, -0.1, -0.008, -0.005, -0.003 \)的情况，而上部分的蓝色曲线，是将\(c_{1}  \)和\(c_{2}  \)都取相反数。可以看到，这两组蓝色的曲线在无穷远处都是平行于红色的曲线(\( c_{1}=0, c_{2}=\pm 1 \))，这个和(3)中讨论的情况一致，主要原因是当\(  t\rightarrow +\infty \)时，\(e^{2 t}  \)最后会支配函数值\( y \)，而其导函数支配\(  y^{\prime}\)。这样的解曲线族被称为【源】(source)，因为最后的函数值都会趋向于无穷，从零点出发。其实相当于这里的所谓的“阻尼”是一个加速物体运动的阻尼，系统最终blow up。

(5) 如果初始的微分方程为\(y^{\prime \prime}+3 y^{\prime}+2 y=0  \)，也就是阻尼项的系数变成正的(类似于物理意义上存在阻尼)，得到的图像和上面一致，只是变成了从外边向原点汇聚，也就是【汇】(Sink)。

例子2    \( y^{\prime \prime}=4 y \)
从特征方程求得\( s_{1}=2, s_{2}=-2 \)，于是\( y=c_{1} e^{2 t}+c_{2} e^{-2 t}, \quad y^{\prime}=2 c_{1} e^{2 t}-c_{2} 2 e^{-2 t} \)。两项中有一项随时间增大，另一项随时间衰减，最终形成的相平面称为【鞍】(Saddle)图。

(1) \(c_{1}=0  \)，\( c_{2} \)取正负，得到的就是\(y=-2y^{\prime} \)直线，而且是随着时间增大，越来越靠近原点；

(2)  \(c_{2}=0  \)，\( c_{1} \)取正负，得到的就是\(y=2y^{\prime} \)直线，而且是随着时间增大，越来越远离原点；
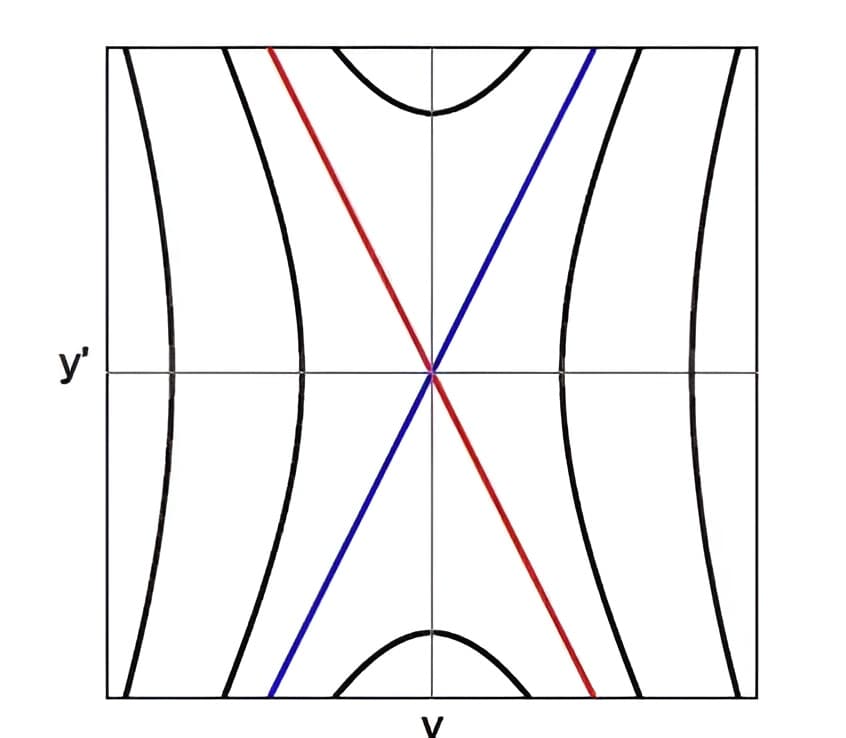(3)  其他取点情况，演进的结果就是当时间越来越大时，更加趋向于\(  y=2y^{\prime}\)。

 

相螺旋和中心

继续研究相平面，也就是\(  y-y^{\prime}\)平面。对于微分方程\( A y^{\prime \prime}+B y^{\prime}+C y=0 \)，我们构造方程的解函数\( y=e^{s t} \)代入原方程求得特征方程\( A s^{2}+B s+C=0 \)，于是可以得到参数\( s \)。这里就是讨论特征方程参数\( B^{2}<4 A C \)的情况，即没有实数解的情况，关于实数解的情况我们前面已经讨论过。得到的复数解\(s=a \pm i \omega  \)，因为虚部的关系，相平面会出现旋转或者螺旋等状态。

因为实部的差异，会有三种不同的相平面的状态：

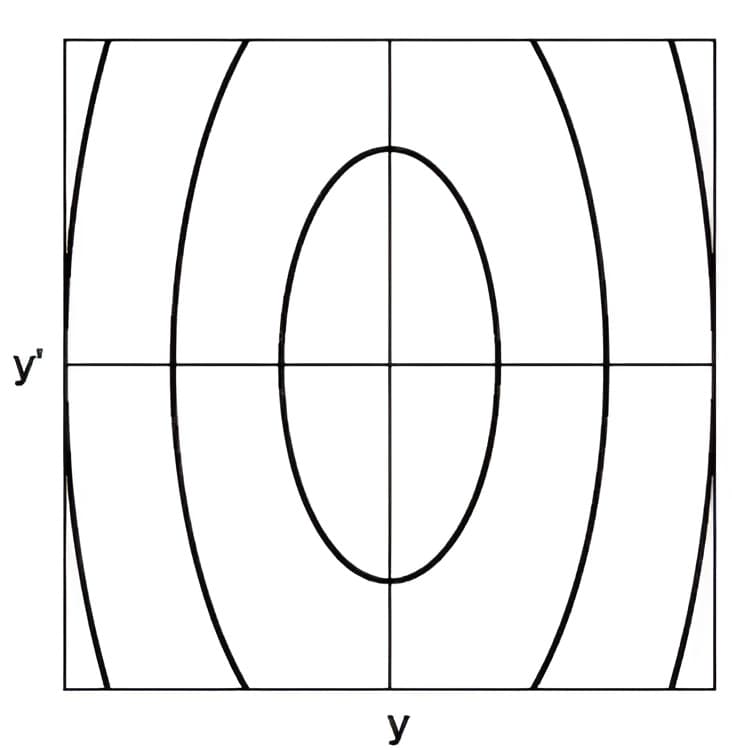
(1) 【中心型】 (\( a=0 \))
也就是参数\(s  \)只存在虚部，那么必有微分方程的阻尼项的系数为零，那么我们可将微分方程写成\(y^{\prime \prime}+\omega^{2} y=0  \)，其解函数为\(  y=c_{1} \cos \omega t+c_{2} \sin \omega t\)。这个方程和解函数描述的是纯振荡过程，例如弹簧重物组(动能和势能之间的无线循环转换)，或者LC振荡电路(没有电阻的存在，那么能量不断地在电感和电容之间互相传递不损耗)，当然这两个描述的都是非常理想的物理模型状态。导函数的解析式为$$y^{\prime}=-c_{1} \omega \sin \omega t+c_{2} \omega \cos \omega t$$很容易发现\( (\omega y)^2+y{\prime}^2=(c_{1}\omega)^2+ (c_{2}\omega)^2\)，也就是椭圆方程，长短轴之比为\(\omega  \)，当引入不同的初始值(即从一个点确定\(\omega  \)和\(c_{1} \)以及\( c_{2} \))，函数会在不同的椭圆曲线上运动，这就是“中心型”相平面图，\(  \)和\(  \)随时间的变化都具有相同的周期性，所描述的运行形式没有能量损失。该结果为“中立稳定”，即曲线既不会随着时间变化发展至无穷，也不会衰减至原点。

(2) 【螺旋】(Spirals)源/汇 (\( a>0 \) or \( a<0 \))
其实这里的\( a<0 \)表示真的存在物理意义上的“阻尼”，或者是是系数\( B>0 \)的情况(二阶导数前面的系数大于零的前提，思考一下一元二次方程的求根公式就知道)；\(a>0  \)表示的意思是存在一个“加速阻尼”，即体系的能量不断没有耗散掉，反而越来越多，当然这不是真实的物理意义上的。对于前面的情况，显然物体最终由于阻尼损耗，稳定下来，即停止运动，而后面一种对应于体系blow up的情况。

举例：微分方程\( y^{\prime \prime} \pm 2 y^{\prime}+2 y=0 \)，特征方程为\(s^{2} \pm 2 s+2=0  \)，解为\( s=-1 \pm i \)和\(s=+1 \pm i  \)，前面对应的是螺旋源型(阻尼项正号)，不稳定，后面的是螺旋汇型(阻尼项负号)，稳定。

阻尼项为正号(真阻尼)：解函数\(  y=e^{-t}\left(c_{1} \cos t+c_{2} \sin t\right)\)
阻尼项为负号(假阻尼)：解函数\( y=e^{t}\left(c_{1} \cos t+c_{2} \sin t\right) \)

首先我们需要知道，在没有\( e \)指数项的时候，\( y-y^{\prime} \)曲线是一个椭圆，对于椭圆的参数方程来说，如果两个坐标都可以写成一个正余弦函数，如果两个值不相互抵消，那么大概率是椭圆方程，只是这个椭圆相对于标准的形式进行了一定角度的旋转。
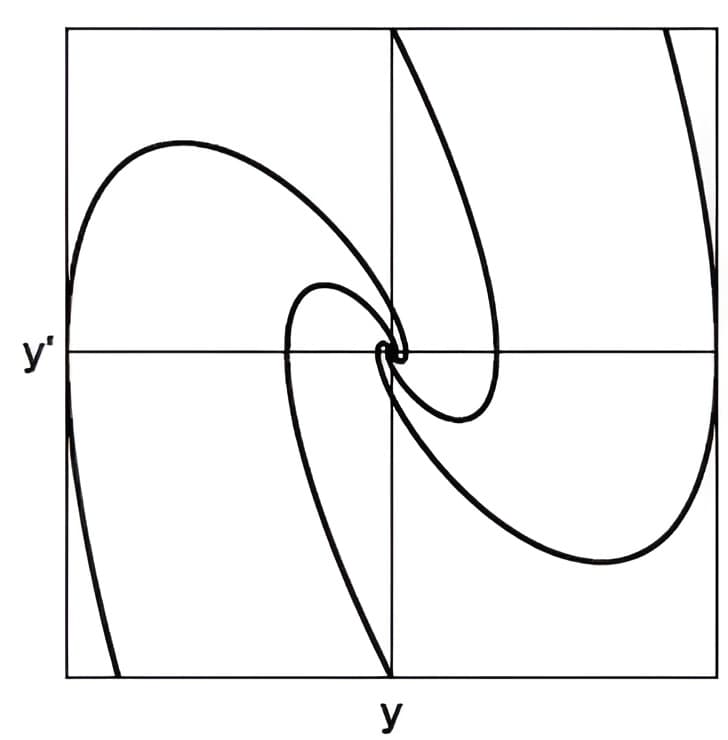对于真阻尼来说，随着时间的增大，曲线上的点越来越靠近原点，同时表达式中的正余弦项保证了曲线的旋转，我们将图像放大或者缩小的到一定的程度，可以观察到和先前完全重合的图像，类似“分型”的概念。从上面的图像，我们无法得知是真阻尼还是假阻尼，必须给定是“衰减”还是“发散”，或者说给曲线加一个箭头方向。

小结：\(  s\)值为实数时，相平面图有三种：源、汇和鞍；\( s \)为复数时，相平面图也有三种：螺旋源、螺旋汇和中心。

 

矩阵与一阶常微分方程的稳定性

Two First Order Equations Stability

例子(1)  先讨论最简单的例子，惯用的常微分方程\( y^{\prime \prime}+B y^{\prime}+C y=0 \)，写成矩阵形式为$$\frac{d}{d t}\left[\begin{array}{l} y \\ y^{\prime} \end{array}\right]=\left[\begin{array}{cc} 0 & 1 \\ -C & -B \end{array}\right]\left[\begin{array}{l} y \\ y^{\prime} \end{array}\right]$$其实第一个方程的作用是凑出举着，反正最终得到的矩阵称为【友矩阵】(companion matrix)。解函数的指数参数\( s_{1} \)和\(s_{2}   \)就是该矩阵的特征值\( \lambda_{1} \)和\(  \lambda_{2}\)。

正如GS老师讲的，其实我们这里是用不同的语言来描述同一件事情，但是本质上都是相通的。从方程的角度，我们知道微分方程的特征方程为\(s^{2}+B s+C=0  \)，根据一元二次方程的性质\( s_{1}+s_{2}=-B, s_{1} s_{2}=C  \)。如果从矩阵的角度，矩阵的特征值\(\lambda_{1}  \)和\(\lambda_{2}  \)，二者的和等于矩阵的迹\( -B \)，二者乘积等于矩阵行列式\(  C\)，这和前面对于参数\( s\)的描述是一致的。因此有\( s_{1} \)和\( s_{2} \)其实就是矩阵的两个特征值\(\lambda_{1}  \)和\( \lambda_{2} \)。

解函数的稳定性取决于\( s_{1} \)和\( s_{2} \)的实部是不是都小于零，下面列出稳定的条件
(1)  方程角度：\(  B>0, C>0\)
(2)  矩阵角度：矩阵\( \left[\begin{array}{cc} 0 & 1 \\ -C & -B \end{array}\right] \)的两个特征值( \( s \))的实部大于零

例子(2)   对于一个任意二阶矩阵\( A=\left[\begin{array}{ll} a & b \\ c & d \end{array}\right]\)构成的微分方程\(\displaystyle\frac{d \mathbf{z}}{d t}=\left[\begin{array}{ll} a & b \\ c & d \end{array}\right] \mathbf{z}\)矩阵的特征值和特征向量满足\(  \boldsymbol{A} \mathbf{x}_{1}=\lambda_{1} \mathbf{x}_{1}\)，方程的解为\(  \mathbf{z}=c_{1} e^{\lambda_{1} t} \mathbf{x}_{1}+c_{2} e^{\lambda_{2} t} \mathbf{x}_{2}\)。

矩阵的迹为\(  T=a+d\)，行列式值为\(D=a d-b c  \)，则有：

 

线性化(Linearization)

临界点线性化

Linearization at Critical Points

前面讨论的都是线性的微分方程的稳定性，对它们来说稳定的解函数就是最终衰减至\( 0 \)，而对非线性微分方程来说，稳定的解函数最终会衰减到一个固定值。

对于非线性微分方程\(  \displaystyle\frac{d y}{d t}=f(y)\)，我们要问什么是临界点(critical point)？在临界点\(  y=Y\)，必有\(f(Y)=0  \)，即该点的导数为零。如果从\( y=Y \)出发，显然函数会稳定在初始点，因为没有任何前进的推力(导数为零)，但是更核心的问题是，如果从其他的函数点出发，那么最后函数是否会趋近于\(  y=Y\)点。用GS老师的话说，就是讨论这个临界点是stable and attractive还是unstable and repulsive？

【线性化】
方法就是在临近\( Y \)值附近对方程进行线性化。此处以单独的微分方程为例，但是实际应用中通常考察的是多个方程组成的微分方程是否稳定。从\(f(y)  \)的图像上看，在\(Y  \)的邻域，如果其导数大于零，则原微分方程不稳定，若导数小于零，则微分方程稳定。在\( Y \)附近的线性近似方程为：$$f(y)=f(Y)+(y-Y) \frac{d f}{d y}(Y)=(y-Y) \frac{d f}{d y}(Y)$$线性化\(\displaystyle\frac{d y}{d t} \approx(y-Y) \displaystyle\frac{d f}{d y}(Y)  \)，等式左侧增加一个常数，$$\frac{d(y-Y)}{d t} \approx(y-Y) \frac{d f}{d y}(Y)$$记\(\displaystyle\frac{d f}{d y}(Y)=a  \)，则可解这个关于\( y-Y \)的微分方程得到\(y-Y \approx C e^{a t}  \)。由此可知\(a<0  \)，则函数\(y-Y  \)随时间增长趋近于零，即\(y  \)趋近于稳态\(Y  \)，反之函数\(  y\)为不稳定状态。

例子：Logistic方程\(\displaystyle\frac{d y}{d t}=3 y-y^{2}  \)
很容易知道两个临界值为\(  Y=0, Y=3\)。由\( \displaystyle\frac{d f}{d y}=3-2 y \)带入两个临界值分别得到\(  3\)和\( -3 \)。因此：
(1)  当\( Y=3 \)时，解函数为稳态，也就是当\( y \)稍微偏离临界值\( Y=3 \)时，\(  y-3 \approx C e^{-3 t}\)，函数最终会会衰减至临界值\( 3 \)；
(2)  当\( Y=0 \)时，解函数为非稳态，也就是说当函数值稍微偏离临界值\(Y=0  \)时，随着时间增长，函数将远离\( 0 \)。

 

方程组的线性化

$$\left\{\begin{aligned} \frac{d y}{d t} &=f(y, z) \\ \frac{d z}{d t} &=g(y, z) \end{aligned}\right.$$对于方程组，求其临界值即求解$$\begin{aligned} &f(Y, Z)=0\\ &g(Y, Z)=0 \end{aligned}$$在\( y \)的导函数中包含\( z \)，而\(  z\)的导函数中包含\(  y\)，两个方程是相互耦合的(关于方程的耦合我们在线性代数中详细讨论了，用对角化的方式解耦)。

 

捕食者-食饵模型

predator-prey

捕食者数量为\( z \)，食饵为\(y  \)。$$\begin{array}{l} d y / d t=y-y z \\ d z / d t=y z-z \end{array}$$捕食者(狐狸)-食饵(兔子)模型为：兔子的数量取决于自身的繁殖能力(与自身数量\(  \)成正比，说明有指数正常的成分)，以及被捕食者的数量(正比于兔子和狐狸的相遇几率\(  yz\))；狐狸的数量取决于捕食状态(二者相遇几率\( yz \))和因为食物缺乏导致或其他自然原因导致的数量下降(正比于\( z \))。让两个导函数为零，得到两组解$$\begin{aligned} &Y=0, Z=0\\ &Y=1, Z=1 \end{aligned}$$在\((Y, Z)  \)点附近的近似线性方程为：$$\begin{aligned} &f(y, z) \approx f(Y, Z)+(y-Y) \frac{\partial f}{\partial y}+(z-Z) \frac{\partial f}{\partial z}=(y-Y) \frac{\partial f}{\partial y}+(z-Z) \frac{\partial f}{\partial z}\\ &g(y, z) \approx g(Y, Z)+(y-Y) \frac{\partial g}{\partial y}+(z-Z) \frac{\partial g}{\partial z}=(y-Y) \frac{\partial g}{\partial y}+(z-Z) \frac{\partial g}{\partial z} \end{aligned}$$雅各比矩阵(在研究经济稳定性方面很重要)$$\boldsymbol{J}=\left[\begin{array}{ll} \partial f / \partial y & \partial f / \partial z \\ \partial g / \partial y & \partial g / \partial z \end{array}\right]=\left[\begin{array}{cc} 1-z & -y \\ z & y-1 \end{array}\right]$$得到矩阵方程$$\frac{d}{d t}\left[\begin{array}{l} y \\ z \end{array}\right]=\boldsymbol{J}\left[\begin{array}{l} y-Y \\ z-Z \end{array}\right]$$下面讨论两个临界点的稳定性
(a)  临界点\(Y=0, Z=0  \)有\( \boldsymbol{J}=\left[\begin{array}{cc} 1 & 0 \\ 0 & -1 \end{array}\right] \)，于是\(  \displaystyle\frac{d}{d t}\left[\begin{array}{l} y \\ z \end{array}\right]=\left[\begin{array}{l} y\\ z \end{array}\right]\)即在狐狸和兔子的基数都很少时(这个临界点附近)，兔子通过正常繁衍而增长(增长速度和自身数量正比，其与捕食者相遇导致的数量减少可以忽略)，而狐狸则会衰减(负指数)，这是一个不稳定的状态。

(b)  临界点\(Y=1, Z=1  \)有\(  \boldsymbol{J}=\left[\begin{array}{cc} 0 & -1 \\ 1 & 0 \end{array}\right]\)，在临界点进行线性化得到$$\begin{aligned} &\frac{d}{d t}\left[\begin{array}{l} y \\ z \end{array}\right]=\boldsymbol{J}\left[\begin{array}{l} y-Y \\ z-Z \end{array}\right]\\ &\Rightarrow \frac{d}{d t}\left[\begin{array}{l} y-Y \\ z-Z \end{array}\right]=J\left[\begin{array}{l} y-Y \\ z-Z \end{array}\right]\\ &\Rightarrow \frac{d}{d t}\left[\begin{array}{l} y-1 \\ z-1 \end{array}\right]=\left[\begin{array}{cc} 0 & -1 \\ 1 & 0 \end{array}\right]\left[\begin{array}{l} y-1 \\ z-1 \end{array}\right] \end{aligned}$$解得$$\frac{d(y-1)}{d t}=-(z-1) ;\quad \frac{d(z-1)}{d t}=(y-1)$$ 我们回忆一下圆的参数方程，如果这里的\( y-1=\cos t \)，而\(  z-1=\sin t\)，那么正好可以满足这个方程组。详细描述：
(1)  如果狐狸的数量超过临界值\( 1 \)，会导致兔子的负增长；
(2)  如果兔子的数量低于临界值\( 1 \)，会导致狐狸的负增长；
(3)  如果狐狸的数量低于临界值\( 1 \)，会导致兔子的正增长；
(4)  又回到状态(1)，如此往复循环.......
这种情况称为【中立型稳定】，在临界点附近保持稳定不远离，也不靠近。在\( y-z \)平面上，\( y \)和\( z\)的值相当于围绕在以\(Y=1, \quad Z=1  \)为圆心，以\( 1 \)为半径的圆上循环转圈。
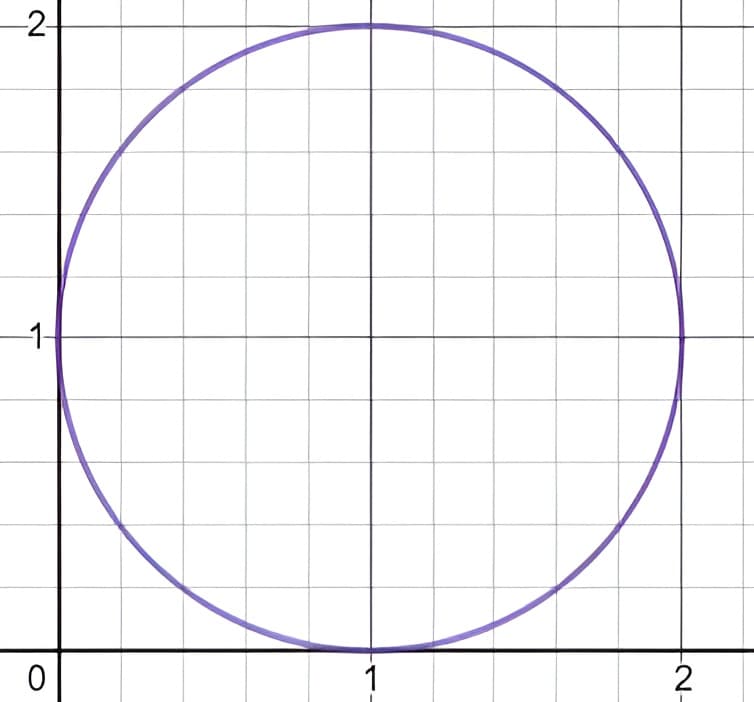实际上对\(\displaystyle\frac{d(y-1)}{d t}=-(z-1)\)再求导之后可得\( y^{\prime \prime}+y=0 \)，这就是振荡方程，由于不存在阻尼项，因此可以无限循环重复振荡，这样描述了这种特殊状态。

 

2阶矩阵的特征值和稳定性

Eigenvalues and Stability 2 by 2 Matrix

特征值
从微分方程\( y^{\prime \prime}+B y^{\prime}+C y=f(t) \)出发，将\(y  \)和其导数\(y^{\prime}  \)这两个元素组成一个列向量，那么对列向量上的这两个元素求导等价于用一个矩阵作用于这个列向量。$$\frac{d}{d t}\left[\begin{array}{l} y \\ y^{\prime} \end{array}\right]=\left[\begin{array}{cc} 0 & 1 \\ -C & -B \end{array}\right]\left[\begin{array}{l} y \\ y^{\prime} \end{array}\right]$$求解矩阵的特征值可以得到方程\(\lambda^{2}+B \lambda+C=0  \)，这就是友矩阵的特征值方程，也是微分方程解函数的指数参数\(  s\)的特征方程。

稳定性
稳定即为解函数\( y \)随着时间演化趋近于\( 0\)，这里就是利用矩阵的特征值来判定微分方程的稳定性。因为解函数具有\(e^{s t}  \)的形式，而\( s \)其实就是矩阵的特征值\(  \lambda\)，因此若\(\lambda_{1}<0, \lambda_{2}<0  \)，或者复特征值\( \lambda=a \pm i \omega \)的实部\(  a<0 \)(注意复数的特征值都是共轭成对出现的)，则函数稳定。

对于二阶矩阵，特征值如果是实数，那么只有当特征值的和小于零，乘积大于零，才能满足稳定条件，同样地，如果特征值是复数，那么由于复数解的共轭特点，同样有特征值和小于零，特征值的乘积\( \lambda_{1} \lambda_{2}=a^{2}+\omega^{2} \)大于零，才能满足稳定条件。例子如下：
\(A=\left[\begin{array}{cc} -2 & 3 \\ 4 & -1 \end{array}\right], \quad \lambda_{1}+\lambda_{2}=-3\, \mathrm{and}\, \lambda_{1} \lambda_{2}=-10  \)，不稳定；
\( A=\left[\begin{array}{cc} -5 & 6 \\ -7 & 1 \end{array}\right], \quad \lambda_{1}+\lambda_{2}=-4 \, \mathrm{and}\,  \lambda_{1} \lambda_{2}=37\)，稳定。

 

3-D翻转实验

The Tumbling Box in 3-D

一本书，在用橡皮筋扎紧的情况下，从三个不同的方向抛出在空中做翻转实验，验证转动状态是否稳定。先上结论：对一本普通的书而言，抛起的方向又三个，其中沿着短轴方向为“中立型稳定”，沿着长轴为“稳定”，而沿着中长轴则是不稳定。描述翻转的运动状态，可以用三种情况下的角动量的物理量进行计算有$$\begin{aligned} &d x / d t=y z\\ &d y / d t=-2 x z\\ &d z / d t=x y \end{aligned}$$这实际上就是三个相互关联的微分方程，求解方法是先找到临界值(所有导函数为零的点)，然后在临界值附近进行线性化。求得临界值附近的导数，最后导数矩阵的特征值会给出稳定性与否的判定。观察得知\(  x d x / d t+y d y / d t+z d z / d t=0\)，积分得到$$\frac{1}{2}\left(x^{2}+y^{2}+z^{2}\right)=C$$这个方程实质上代表翻转过程中的能量守恒。从第一个和第二个微分方程组合可以得到\(  2 x d x / d t+y d y / d t=0\)，积分得到\(  x^{2}+\frac{1}{2} y^{2}=C\)，表示方程的解对\(  x-y\)平面来说是一个椭圆。同样的方法组合第二和第三个方程然后积分有$$z^{2}+\frac{1}{2} y^{2}=C$$继续分析有$$x^{2}-z^{2}=C$$而这时一个双曲线方程(hyperbola wander away )，它会趋向于无限，这部分就是不稳定的状态(响应)。

求解临界值就是让前面的三个微分方程都等于零，于是可以解得\((\pm 1,0,0), \quad(0,\pm 1,0), \quad(0,0,\pm 1), \quad  (0,0,0)\)，前面三个代表沿着某一轴旋转，最后一个代表静止。方程的雅各比矩阵$$\boldsymbol{J}=\left[\begin{array}{ccc} 0 & z & y \\ -2 z & 0 & -2 x \\ y & x & 0 \end{array}\right]$$它的特征值决定了解函数的稳定性。
(1)   沿着短轴旋转，即代入\(  (1,0,0)\)，求得\(\boldsymbol{J}=\left[\begin{array}{ccc} 0 & 0 & 0 \\ 0 & 0 & -2 \\ 0 & 1 & 0 \end{array}\right]  \)，特征值为\( 0, \, \pm\sqrt{2} i\)，因此是“中立型稳定”。
(2)   沿着短轴旋转，即代入\(  (0,0,1)\)，求得特征值为\(0, \, \pm\sqrt{2}   \)，因此是“稳定”。
(3)   沿着中轴旋转，即代入\( (0,1,0) \)，求得\(\boldsymbol{J}=\left[\begin{array}{lll} 0 & 0 & 1 \\ 0 & 0 & 0 \\ 1 & 0 & 0 \end{array}\right]  \)，特征值为\( 0, \, \pm 1\)，因此是“不稳定”。其实对应是前面的双曲线方程\(  \)，旋转的时候hyperbola wander away from the  point \( (0,1,0) \).

问：数值解法?
答：
待补充
https://zhuanlan.zhihu.com/p/46533077