马尔科夫矩阵和傅里叶级数
马尔科夫矩阵
矩阵中任意元素都是非负的，而且每列的元素加和为\( 1\)的矩阵称为【马尔可夫矩阵】(Markov matrices)。马尔科夫矩阵主要应用在概率领域，将一个马尔科夫矩阵进行方幂运算得到的仍旧是马尔科夫矩阵。$$A=\left[\begin{array}{ccc} 0.1 & 0.01 & 0.3 \\ 0.2 & 0.99 & 0.3 \\ 0.7 & 0 & 0.4 \end{array}\right]$$ 当处理一个微分方程问题的时候，特征值\(0 \)意味着得到一个稳态。当进行矩阵的方幂运算时，特征值给出稳态的条件包括：
(1) \(\lambda_{1}=1 \)是特征值之一；
(2) 其它特征值的绝对值都比\(1 \)小，\( \left|\lambda_{i}\right|<1\)。
我们再来分析一下前面的矩阵\(A \)，由于每一列的加和都为\( 1\)，那么对矩阵\(A- I \)来说每一列的加和都是\(0 \)，于是矩阵\(A- I \)的三个行向量是线性相关的，矩阵为奇异阵，其行列式\(det(A- I) =0\)，因此\( 1\)是矩阵\(A \)的特征值。我们知道\([1\,1\,1](A-I)=0 \)两边取转置有\( (A^{\mathrm{T}}-I)\left[\begin{array}{l} 1 \\ 1 \\ 1 \end{array}\right]=0\)，于是\( \left[\begin{array}{l} 1 \\ 1 \\ 1 \end{array}\right]\)属于矩阵\( A-I\)的左零空间\(\operatorname{N}((\boldsymbol{A}-I)^{\mathrm{T}}) \)，或者说矩阵\(\boldsymbol{A}^{\mathrm{T}}-I \)的零空间，或者说\( \left[\begin{array}{l} 1 \\ 1 \\ 1 \end{array}\right]\)是矩阵\((\boldsymbol{A}-I)^{\mathrm{T}} \)对应于特征值\( 1\)的特征向量。其实我们简单想一下就知道，既然\(A-I \)的每一行加和都为零，那么整体转置以后，就变成了每一列的加和为零，于是\(\left[\begin{array}{l} 1 \\ 1 \\ 1 \end{array}\right] \)就是矩阵\(\boldsymbol{A}^{\mathrm{T}}-I \)的零空间向量。$$A-I=\left[\begin{array}{rrr} -.9 & .01 & .3 \\ .2 & -.01 & .3 \\ .7 & 0 & -.6 \end{array}\right]$$容易求解出\(A-I \)的零空间，即对应于特征值\( 1\)的特征向量。解得\(\mathbf{x}_{1}=\left[\begin{array}{c} 0.6 \\ 33 \\ 0.7 \end{array}\right] \)
如果矩阵有\( n\)个线性无关的特征向量，则有：$$\mathbf{u}_{\mathbf{k}}=A^{\mathbf{k}} \mathbf{u}_{0}=c_{1} \lambda_{1}^ \mathbf{k} \mathbf{x}_{1}+c_{2} \lambda_{2}^{\mathbf{k}} \mathbf{x}_{2}+\ldots+\mathrm{c}_{\mathbf{n}} \lambda_{\mathbf{n}}^{\mathbf{k}} \mathbf{x}_{\mathbf{n}}$$如果\( \lambda_{1}=1\)并且其他特征值都小于\(1 \)，则系统在\( \mathbf{k}\)增大过程中，\(\mathbf{u}_{\mathbf{k}} \)越来越趋近于\( \mathbf{u}_{\mathbf{0}}\)的分量\( c_{1} \mathbf{x}_{1}\)，即给出了一个稳态情况。这里的特征向量\(\mathbf{x}_{1} \)的每一个分量都是正的，因此若初始值为正，那么最终的稳态也都是正值。
人口流动与【马尔科夫矩阵】
$$\left[\begin{array}{c} u_{\text {Cal}} \\ u_{\text {Mass}} \end{array}\right]_{t=k+1}=\left[\begin{array}{cc} .9 & .2 \\ .1 & .8 \end{array}\right]\left[\begin{array}{c} u_{\text {Cal}} \\ u_{\text {Mass}} \end{array}\right]_{t=k}$$左边的列向量分别表示加州和麻州的人口，等式右边的矩阵的每一列元素代表着人口的去留比例。\( 0.9\)的加州人继续留在加州，\( 0.2\)的麻州人转移到加州；\( 0.1\)的加州人转移到麻州，\( 0.8\)的麻州人继续留在麻州。列向量的和都是\( 1\)保证整体人口的平衡。当然在这个变化过程中不会出现负元素。
取初值\( \left[\begin{array}{c} u_{C a l} \\ u_{\text {Mass}} \end{array}\right]_{0}=\left[\begin{array}{c} 0 \\ 1000 \end{array}\right]\)，一次迁徙之后有$$\left[\begin{array}{c} u_{\text {Cal}} \\ u_{\text {Mass}} \end{array}\right]_{1}=\left[\begin{array}{cc} .9 & .2 \\ .1 & .8 \end{array}\right]\left[\begin{array}{c} 0 \\ 1000 \end{array}\right]=\left[\begin{array}{c} 200 \\ 800 \end{array}\right]$$求得两个特征值分为\( 1\)和\( 0.7\)，对应的特征矩阵为\(\mathbf{x}_{1}=\left[\begin{array}{l} 2 \\ 1 \end{array}\right], \mathbf{x}_{2}=\left[\begin{array}{c} 1 \\ -1 \end{array}\right] \)。我们先前已经讨论了，特征值\(1 \)对应的特征向量就是系统稳定时候的状态，于是推出稳态时，加州的人口数是麻州的人口数的两倍。系统的通解为$$\mathbf{u}_{\mathbf{k}}=\mathbf{S} \Lambda^{k} \mathbf{S}^{-1} \mathbf{u}_{\mathbf{0}}=\mathbf{S} \Lambda^{k}\left(\mathbf{S}^{-1} \mathbf{u}_{\mathbf{0}}\right)=\mathbf{S} \Lambda^{k} \mathbf{c}=\left[\begin{array}{cc} 2 & 1 \\ 1 & -1 \end{array}\right]\left[\begin{array}{cc} c_{1} \\ 0.7^{k} c_{2} \end{array}\right]=c_{1}\left[\begin{array}{l} 2 \\ 1 \end{array}\right]+c_{2}(0.7)^{k}\left[\begin{array}{c} 1 \\ -1 \end{array}\right]$$
傅里叶变换的矩阵理解
对于\( \mathbf{R}^{\mathrm{n}}\)空间来说，如果有一组标准正交基\(\mathbf{q}_{1}, \mathbf{q}_{2} \ldots \mathbf{q}_{\mathbf{n}} \)，则任意向量\( \mathbf{v}\)可以写成$$\mathbf{v}=\mathbf{x}_{1} \mathbf{q}_{1}+\mathbf{x}_{2} \mathbf{q}_{2} \ldots \ldots \mathbf{x}_{\mathrm{n}} \mathbf{q}_{\mathrm{n}}$$其中系数\(\mathbf{x}_{i} =\mathbf{q_{i}^{T}} \mathbf{v}\)，而$$\mathbf{v}=\left[\begin{array}{lll} \mathbf{q}_{1} & \cdots & \mathbf{q}_{n} \end{array}\right]\left[\begin{array}{c} x_{1} \\ \vdots \\ x_{n} \end{array}\right]=\mathbf{Qv}\, \Rightarrow \, \mathbf{x}=\mathbf{Q^{-1}v}$$我们知道\(\mathbf{Q} \)是正交矩阵，根据正交矩阵的性质有\(\mathbf{Q}^{-1}=\mathbf{Q^{T}} \)，于是\(\mathbf{x}=\mathbf{Q^{T}v} \)，这个结果和我们之前的\( \mathbf{x}_{i} =\mathbf{q_{i}^{T} }\mathbf{v}\)是异曲同工的。
标准正交是此处的核心概念，而傅里叶级数也是在这个概念上构建的，我们可以对任意函数作傅里叶展开，得到表达式：$$f(x)=a_{0}+a_{1} \cos x+b_{1} \sin x+a_{2} \cos 2 x+b_{2} \sin 2 x+\cdots$$与之前的有限个标准正交的向量组成的正交矩阵不同，这个空间是无限维，它的基是无数组连续函数。
此处正交概念与\( \mathbf{R}^{n}\)空间不同，点积的概念也不同，相当于一个离散的变成了一个无穷连续的。
(1) 向量 \( \mathbf{v}^{\mathrm{T}} \mathbf{w}=\mathbf{v}_{1} \mathbf{w}_{1}+\mathbf{v}_{2} \mathbf{w}_{2}+\ldots \ldots+\mathbf{v}_{\mathbf{n}} \mathbf{w}_{\mathbf{n}}\)
(2) 函数 \(f^{\mathrm{T}} g=\displaystyle\int_{0}^{2 \pi} f(x) g(x) d x\)
求解\(\cos x\)基前面的系数方法如下$$ \begin{aligned} \int_{0}^{2 \pi} f(x) \cos x d x &=\int_{0}^{2 \pi}\left(a_{0}+a_{1} \cos x+b_{1} \sin x+a_{2} \cos 2 x+\cdots\right) \cos x d x \\ &=0+\int_{0}^{2 \pi} a_{1} \cos ^{2} x d x+0+0 \cdots \\ &=a_{1} \pi \end{aligned} $$因此\(a_{1}=\displaystyle\frac{1}{\pi} \int_{0}^{2 \pi} f(x) \cos x d x\)，其他基前面的系数的求解方法也和这个类似。
复习二
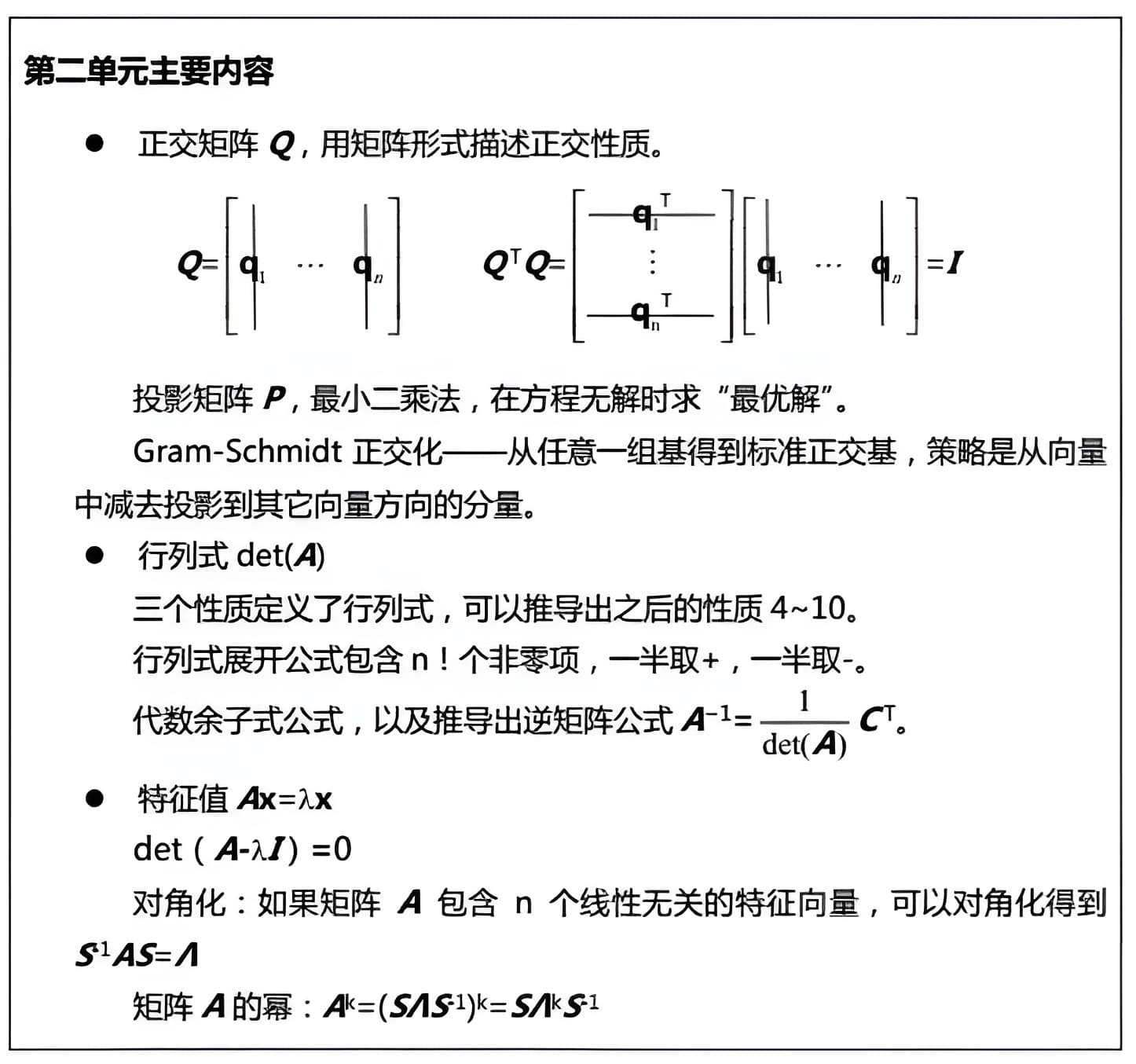
复习题1. \(\mathbf{a}=\left[\begin{array}{l} 2 \\ 1 \\ 2 \end{array}\right] \)
(a) 求解投影到向量\(\mathbf{a} \)方向的投影矩阵\(P \)？
\(P=A\left(A^{\mathrm{T}} A\right)^{-1} A^{\mathrm{T}} \)，这里\(\mathbf{a} \)是向量，计算起来就容易得多，因此有$$P=\frac{a a^{T}}{a^{T} a}=\frac{1}{9}\left[\begin{array}{lll} 4 & 2 & 4 \\ 2 & 1 & 2 \\ 4 & 2 & 4 \end{array}\right]$$
(b) 求矩阵\( P\)的秩？
第二列和第三列是第一列的倍数，所以矩阵的秩为\( 1\)。或者从投影矩阵投影的空间是\(1 \)维可以判断出来。进一步解释一下这句话：如果投影矩阵的秩大于\(1 \)，也就是矩阵\( P\)中至少有两个列向量是线性无关的，那么对于任意向量来说，经过投影矩阵的作用之后，投影出来的向量的方向肯定不止一种，比如说我们选定两个向量都是其他元素都是零，但是对应于\( P\)中线性无关的列向量的系数为\( 1\)(各选一个)。
(c) 矩阵\( P\)的列空间？
列空间就向量\( \mathbf{a}\)所在的直线。应该这样理解：将矩阵\( P\)作用于所有向量，就得到了矩阵\(P \)的列空间，显然这个列空间就是投影空间，也就是向量\( \mathbf{a}\)所在的直线。
(d) 矩阵\( P\)的特征值？
矩阵的秩为\( 1\)，因此存在二重特征值\(0 \)，再从矩阵的迹可以得到另一个特征值为\(1 \)，因此特征值为\( 1, \, 0, \, 0\)。
再详细讲一下：秩为\( 1\)，那么对于方程\(Px=b \)方程的主元(pivot)只有一个，自由变量有两个，分别给两个自由变量赋值\( 1\),就会得到两个线性无关的列向量共同张成了矩阵\( P\)的零空间。而我们前面在“转置之后矩阵特征值和特征向量的变化”已经讨论过，\( A-\lambda I\)的零空间和\( A\)的特征向量是对应的。这里我们的\( \lambda=0\)，于是\( A\)的零空间正好对应于二重特征值\( 0\)的特征向量空间，于是正好是两个线性无关的向量张成的。
(e) 求矩阵\( P\)对应特征值\(1 \)的特征向量？
特征值为\( 1\)说明投影之后是其自身，因此\( \mathbf{a}\)就是对应的特征向量。
(f) 若有\( \mathbf{u}_{\mathbf{k}+1}=P \mathbf{u}_{\mathbf{k}}\)，且有初值\( \mathbf{u}_{0}=\left[\begin{array}{l} 9 \\ 9 \\ 0 \end{array}\right]\)，求\( \mathbf{u}_{\mathbf{k}}\)？
每进行一次迭代，相当于对原有的列向量进行一次投影操作，投影到\(\mathbf{a}\)方向上，但是显然投影一次之后，再投影的话，得到的都是自己，也就是“自己投影自己”。从第二次开始，投影值不发生变化，于是有$$\mathbf{u}_{\mathrm{k}}=P^{\mathrm{k}} \mathbf{u}_{0}=P \mathbf{u}_{0}=\mathbf{a} \frac{\mathbf{a}^{\mathrm{T}} \mathbf{u}_{0}}{\mathbf{a}^{\mathrm{T}} \mathbf{a}}=3 \mathbf{a}=\left[\begin{array}{l} 6 \\ 3 \\ 6 \end{array}\right]$$
(g) 测验中可能出现\(\mathbf{u}_{\mathbf{k}+1}=A \mathbf{u}_{\mathbf{k}} \)，其中的矩阵\( A\)不是投影矩阵，没有投影矩阵的性质\( P^{\mathbf{k}} \mathbf{u}_{0}=P \mathbf{u}_{0}\)，求表示式的通解？
首先我们应该重新说明一下先前推导的一个式子$$\mathbf{u}_{\mathbf{k}}=\mathbf{S} \Lambda^{k} \mathbf{S}^{-1} \mathbf{u}_{\mathbf{0}}=\mathbf{S} \Lambda^{k}\left(\mathbf{S}^{-1} \mathbf{u}_{\mathbf{0}}\right)=\mathbf{S} \Lambda^{k} \mathbf{c}=\mathbf{S} (\Lambda^{k} \mathbf{c})$$这种推导很直观和简洁，但是我们要注意这里存在一个条件，就是矩阵\(\mathbf{S} \)必须是可逆的，也就是说\(n \)个特征向量组成的矩阵\( \mathbf{S} \)的列向量必须是线性无关的。虽然绝大多数矩阵都满足这个条件，但是仍然存在少部分不满足，所以这个推导不是普适性的。另一方面，我们来看看在前面对矩阵的对角化和差分方程的讨论，其实我们给出的\( \mathbf{u}_\mathbf{k}\)的定义式是\(\mathbf{u}_{\mathbf{k}}=A^{\mathbf{k}} \mathbf{u}_{0}=\mathbf{c}_{1} \lambda_{1}^{k} \mathbf{x}_{1}+\mathbf{c}_{2} \lambda_{2}^{k} \mathbf{x}_{2}+\ldots+\mathbf{c}_{n} \lambda_{n}^{k} \mathbf{x}_{n}=\mathbf{S} \Lambda^{k} \mathbf{c} \)并不要求矩阵\( \mathbf{S}\)可逆。所以无论\(\mathbf{S} \)是否可逆，一定有\( \mathbf{u}_{\mathbf{k}}=\mathbf{S} \Lambda^{k} \mathbf{c}\)，我们前面推导利用到的\( \mathbf{S}^{-1} \)只是\( \mathbf{S}\)可逆情况下的一种推导方式，当然最后肯定是殊途同归。
开始答题：这个时候就需要求解特征值和特征向量，\(\mathbf{u}_{0}=\mathbf{c}_{1} \mathbf{x}_{1}+\mathbf{c}_{2} \mathbf{x}_{2}+\mathbf{c}_{3} \mathbf{x}_{3} \)，则\( \mathbf{u}_{\mathbf{k}}=\mathrm{c}_{1} \lambda_{1}^{\mathbf{k}} \mathbf{x}_{1}+\mathrm{c}_{2} \lambda_{2}^{\mathbf{k}} \mathbf{x}_{2}+\mathrm{c}_{3} \lambda_{3}^{\mathbf{k}} \mathbf{x}_{3}=\mathbf{S} \Lambda^{k} \mathbf{c}\)。对于投影矩阵来说有\( \lambda_{1}=1, \lambda_{2}=\lambda_{3}=0\)，于是\( \mathbf{u}_{1}=\mathbf{u}_{2}=\mathbf{u}_{3}=\ldots \ldots\)
复习题2. 已知以下数据点\( \begin{array}{|l|l|} \hline t & y \\ \hline 1 & 4 \\ \hline 2 & 5 \\ \hline 3 & 8 \\ \hline \end{array}\)
(a) 利用这三个点拟合过原点的一条直线\( y=D t\)？
如果在不考虑过原点的情况下的最优解，方程为\( \left[\begin{array}{l} 1 \\ 2 \\ 3 \end{array}\right] \left[\begin{array}{l} M\\ N \end{array}\right] =\left[\begin{array}{l} 4 \\ 5 \\ 8 \end{array}\right]\)。现在我们求解的是过原点的最优解，于是\(\left[\begin{array}{l} 1 \\ 2 \\ 3 \end{array}\right] D=\left[\begin{array}{l} 4 \\ 5 \\ 8 \end{array}\right] \)。
假设方程的最优解为\(\hat{D} \)，根据\( \boldsymbol{A}^{\mathrm{T}} \boldsymbol{A} \hat{D}=\boldsymbol{A}^{T} \mathbf{b}\)求得\( \hat{D}=19 / 7\)，因此解析式为\(y=(19 / 7) t \)。
(b) 怎样从投影来理解这个问题？
对于最小二乘法有两种理解方法，其中一种是找到平面内最优的一条直线。另一种是将\(\mathbf{b}=\left[\begin{array}{l} 4 \\ 5 \\ 8 \end{array}\right] \)投影到\(A \)空间，从而求得最接近\( A \mathbf{x}=\mathbf{b}\)的解。
复习题3. 向量\( \mathbf{a}_{1}=\left[\begin{array}{l} 1 \\ 2 \\ 3 \end{array}\right] ,\quad \mathbf{a}_{2}=\left[\begin{array}{l} 1 \\ 1 \\ 1 \end{array}\right]\)确定了一个平面，找到该平面的一组正交基？
根据前面我们学习的格拉姆-施密特正交化的方法，我们知道，求解正交基的方法是，先取\( \mathbf{a}_{1}\)为一个基，然后再求其正交方向的向量。处理方法是先将\( \mathbf{a}_{2}\)经过投影矩阵的作用投影到\( \mathbf{a}_{1}\)上，然后用\( \mathbf{a}_{2}\)减去与其正交的投影部分，就得到了垂直于\(\mathbf{a}_{1} \)的分量。$$\mathbf{B}=\mathbf{a}_{2}-\frac{\mathbf{a}_{1}^{\mathrm{T}} \mathbf{a}_{2}}{\mathbf{a}_{1}^{T} \mathbf{a}_{1}} \mathbf{a}_{1}=\left[\begin{array}{c} 4 / 7 \\ 1 / 7 \\ -2 / 7 \end{array}\right]$$
复习题4. 已知一个\( 4\)阶方阵具有特征值\( \lambda_{1}, \lambda_{2}, \lambda_{3}, \lambda_{4} \)。
(a) 特征值满足什么条件才能保证\(A \)为可逆矩阵？
当特征值均不为零时，矩阵\( A\)可逆。“一个矩阵是奇异矩阵”和“零是该矩阵的特征值”是等价的。如果有特征值是零，说明矩阵本身的行列式等于零(或者说列向量不是线性无关)，显然就不可逆(零空间有非零向量)。
(b) 求逆矩阵行列式的值？
\( A^{-1}\)的特征值为\( A\)特征值的倒数(\( (A-\lambda I)^{-1}=A^{-1}-\frac { I }{\lambda } \))，因此\(\operatorname{det}\left(A^{-1}\right)=\frac{1}{\lambda_{1}} \frac{1}{\lambda_{2}} \frac{1}{\lambda_{3}} \frac{1}{\lambda_{4}} \)。
(c) 求\((A+I) \)的迹？
\((A+I) \)的特征值是\(\lambda_{1}+1, \lambda_{2}+1, \lambda_{3}+1, \lambda_{4}+1 \)，该矩阵的迹为\( \lambda_{1}+\lambda_{2}+\lambda_{3}+\lambda_{4}+4 \)。
复习题5. 已知三对角矩阵$$A_{4}=\left[\begin{array}{llll} 1 & 1 & 0 & 0 \\ 1 & 1 & 1 & 0 \\ 0 & 1 & 1 & 1 \\ 0 & 0 & 1 & 1 \end{array}\right]$$令\( \mathrm{D}_{\mathrm{n}}=\operatorname{det}\left(\boldsymbol{A}_{\mathrm{n}}\right)\)
(a) 用代数余子式的方法求\(\mathrm{D}_{\mathrm{n}}=\mathrm{aD}_{\mathrm{n}-1}+\mathrm{bD}_{\mathrm{n}-2} \)里面的系数？
根据代数余子式的方法求得\( \mathrm{D}_{4}=(1) \mathrm{D}_{3}+(-1) \mathrm{D}_{2}\)。
(b) 利用找到的递归方程\(\mathrm{D}_{\mathrm{n}}=\mathrm{a} \mathrm{D}_{\mathrm{n}-1}+\mathrm{b} \mathrm{D}_{\mathrm{n}-2} \)，求\(\mathrm{D}_{\mathrm{n}} \)？
把它当作方程组来求解，我们首先得到初值\( D_{1}=1, D_{2}=0\)。按照递归方程构造二阶线性方程\(\left[\begin{array}{c} D_{n} \\ D_{n-1} \end{array}\right]=\left[\begin{array}{cc} 1 & -1 \\ 1 & 0 \end{array}\right]\left[\begin{array}{c} D_{n-1} \\ D_{n-2} \end{array}\right] \)，求解矩阵的特征值可得\( \lambda=\displaystyle\frac{1 \pm \sqrt{3} i}{2}=\mathrm{e}^{ \pm \mathrm{i} \pi / 3}\)，均为模为\( 1\)的复数，在单位圆上旋转(两个特征在旋转)。可以看到\( \lambda_{1}^{6}=\lambda_{2}^{6}=1\)，矩阵经过六次变换之后变为单位阵。该序列既不发散也不收敛，数列以\( 6\)次为重复周期不停循环\( 1,0,-1,0,1,1\)。
我们在“如何进行矩阵的幂运算”这个问题中，谈到了如果\(\lambda \)\)是矩阵\( A\)的特征值，那么矩阵\(A^{n} \)的特征值是\( \lambda^{n}\)。根据\(\mathbf{u}_{\mathbf{k}}=A^{\mathbf{k}} \mathbf{u}_{0}=\mathbf{c}_{1} \lambda_{1}^{k} \mathbf{x}_{1}+\mathbf{c}_{2} \lambda_{2}^{k} \mathbf{x}_{2}+\ldots+\mathbf{c}_{n} \lambda_{n}^{k} \mathbf{x}_{n}=\mathbf{S} \Lambda^{k} \mathbf{c} \)，我们知道每迭代一次其实都是变化这里的\(\Lambda^{k} \)，而\( \Lambda^{1}=\Lambda^{6}\)的，在我们讨论的例子中。
复习题6. 有一组对称矩阵$$A_{2}=\left[\begin{array}{ll} 0 & 1 \\ 1 & 0 \end{array}\right] A_{3}=\left[\begin{array}{lll} 0 & 1 & 0 \\ 1 & 0 & 2 \\ 0 & 2 & 0 \end{array}\right] A_{4}=\left[\begin{array}{llll} 0 & 1 & 0 & 0 \\ 1 & 0 & 2 & 0 \\ 0 & 2 & 0 & 3 \\ 0 & 0 & 3 & 0 \end{array}\right]$$
(a) 找到投影到\(A_{3} \)列空间的投影矩阵\( P\)？
矩阵\( A_{3}\)为奇异矩阵，其列向量构成的空间是一个平面。取其前两列构成矩阵\( A\)，那么向矩阵\( A_{3}\)投影其实就是向矩阵\(A \)投影，两个矩阵的列空间表示的是同一个空间。于是有投影矩阵$$P=A\left(A^{\mathrm{T}} A\right)^{-1} A^{\mathrm{T}}=\left[\begin{array}{rrr} 1 / 5 & 0 & 2 / 5 \\ 0 & 1 & 0 \\ 2 / 5 & 0 & 4 / 5 \end{array}\right]$$可以试试\( A_{3}\)矩阵投影是不是得到自身来验算。
(b) 求\(A_{3} \)的特征值和特征向量？$$\operatorname{det}\left(A_{3}-\lambda I\right)=\left|\begin{array}{ccc} -\lambda & 1 & 0 \\ 1 & -\lambda & 2 \\ 0 & 2 & -\lambda \end{array}\right|=-\lambda^{3}+5 \lambda=0\, \Rightarrow \,\lambda_{1}=0, \lambda_{2}=\sqrt{5}, \lambda_{3}=-\sqrt{5}$$可以用矩阵的迹做检查。$$\left(A_{3}-\lambda I\right) x=0\,\Rightarrow \,\mathbf{x}_{1}=\left[\begin{array}{c} -2 \\ 0 \\ 1 \end{array}\right], \mathbf{x}_{2}=\left[\begin{array}{c} 1 \\ -\sqrt{5} \\ 2 \end{array}\right], \mathbf{x}_{3}=\left[\begin{array}{c} 1 \\ \sqrt{5} \\ 2 \end{array}\right]$$
(c) 找到投影到\(A_{4} \)列空间的投影矩阵\( P\)？
代数余子式展开得到\(\operatorname{det}\left(A_{4}\right)=9 \)，说明矩阵\(A_{4} \)不是奇异阵，因此其列向量空间就是\(\mathbf{R}^{4} \)空间，所以投影矩阵\(P=I \)。
对称矩阵/正定矩阵/二次型
对称矩阵
对称矩阵\(A=A^{\mathrm{T}} \)的特点：矩阵的特性往往可以从其特征值和特征向量表现出来。比如我们先前提到的马尔科夫矩阵，\( 1\)一定是其特征值。对称矩阵主要有下面三条性质：
(1) 所有的特征值都是实数；
(2) 可以"选出"一套完全正交的特征向量
这个性质我们先前讨论过“为什么对称矩阵的特征向量正交？”，更严格的说法是对称矩阵一定可以选出相互正交的特征向量，下面复制先前的证明过程。
设\( \lambda_{1}\)和\( \lambda_{2}\)是一个对称矩阵的特征值，对应的特征向量分别是\(\mathbf{x}_{1} \)和\(\mathbf{x}_{2} \)。于是\( A \mathbf{x}_{1}=\lambda \mathbf{x}_{1}\)，两边同时乘以\(\mathbf{x}_{2} \)，于是\(\mathbf{x}_{2}^{\mathrm{T}} \boldsymbol{A} \mathbf{x}_{1}=\lambda_{1} \mathbf{x}_{2}^{\mathrm{T}} \mathbf{x}_{1} \)，而\(\mathbf{x}_{2}^{\mathrm{T}} \boldsymbol{A} \mathbf{x}_{1}=\left(\boldsymbol{A}^{\mathrm{T}} \mathbf{x}_{2}\right)^{\mathrm{T}} \mathbf{x}_{1}=\lambda_{2} \mathbf{x}_{2}^{\mathrm{T}} \mathbf{x}_{1} \)。因此有\( \left(\lambda_{1}-\lambda_{2}\right) \mathbf{x}_{2}^{\mathrm{T}} \mathbf{x}_{1}=0\)，而两个特征值不相等，因此只会是两个特征向量相互正交。
上述讨论是针对不同特征值的典型情况(每一个特征值对应的特征向量空间是一维的)，但还是有可能存在重复的特征值。重复的特征值，对应的特征向量，应该有两种情况。一种是特征项量短缺的“退化矩阵”，我们先前讨论过了，但是应该对于对称矩阵不存在这种情况；另一种是有多个特征向量的情况，比如二重特征值对应两个特征向量，于是这两个特征项向量张成了一个平面，相当于是“一整个平面的特征向量”，在这个平面上我们可以选择相互垂直的向量。
(3) 可对角化/分解的对称性
利用 \(A=S \Lambda S^{-1} ,\quad A=A^{\mathrm{T}}\)可以知道\( \)，如果正如我们在(2)中提到的，如果选择的\(S \)是一套正交的特征向量的话，当我们把这一套特征向量矩阵\( S\)进行列向量模长归一化，就会得到标准正交矩阵\(Q \)(矩阵的逆等于转置)，于是有\( A=Q \Lambda Q^{-1}=Q \Lambda Q^{\mathrm{T}}\)。这个公式本身也显示了矩阵的对称性，矩阵能够进行这种分解(对角化)，在数学上成为【谱定理】(spectral theorem)，将特征值视为“谱”，在物理上称之为“主轴定理”(补充)。
对称矩阵的特征值都是实数
\( A \mathbf{x}=\lambda \mathbf{x}\)，如果我们讨论的矩阵\( A\)是实矩阵，而特征值\(\lambda \)是复数的话，则取共轭之后有\(A \bar{\mathbf{x}}=\bar{\lambda} \bar{\mathbf{x}} \)，两边取转置有\( \overline{\mathbf{x}}^{\mathrm{T}} \boldsymbol{A}^{\mathrm{T}}=\overline{\mathbf{x}}^{\mathrm{T}} \bar{\lambda}\)，然后同时右乘\( \mathbf{x}\)。根据矩阵\( A\)对称的性质，有\( \overline{\mathbf{x}}^{\mathrm{T}} \lambda \mathbf{x}=\overline{\mathbf{x}}^{\mathrm{T}} \bar{\lambda} \mathbf{x}\)。因此如果\(\overline{\mathbf{x}}^{\mathrm{T}} \mathbf{x} \neq 0 \)，则\( \lambda_{=} \bar{\lambda}\)，于是这个特征值一定就是实数，虚部为零。点积其实是模长的平方:$$\overline{\mathbf{x}}^{\mathrm{T}} \mathbf{x}=\left[\begin{array}{cccc} \bar{x}_{1} & \bar{x}_{2} & \bar{x}_{3} & \bar{x}_{4} \end{array}\right]\left[\begin{array}{c} x_{1} \\ x_{2} \\ x_{3} \\ x_{4} \end{array}\right]=\left|x_{1}\right|^{2}+\left|x_{2}\right|^{2}+\left|x_{3}\right|^{2}+\left|x_{4}\right|^{2}$$GS说什么样的矩阵叫作“好矩阵”也就是满足(1) 所有的特征值都是实数；(2) 可以“选出”一套完全正交的特征向量。如果矩阵\( A\)是一个实对称阵，那么肯定满足这个条件，如果\( A\)是一个复数型对称矩阵呢？那么只有当\( \overline{\boldsymbol{A}}^{\mathrm{T}}=\boldsymbol{A}\) 才是一个“好矩阵”。我们接触到的矩阵中\( 99 \%\)都是实数矩阵，复数对称矩阵在量子力学中涉及的比较多。
对于对称矩阵，有\(A=Q \Lambda Q^{-1}=Q \Lambda Q^{\mathrm{T}} \)，可以写作$$\begin{aligned} \boldsymbol{A}=\boldsymbol{Q} \Lambda \boldsymbol{Q}^{\mathrm{T}} &=\left[\begin{array}{llll} \mathbf{q}_{1} & \mathbf{q}_{2} & \cdots & \mathbf{q}_{n} \end{array}\right]\left[\begin{array}{cccc} \lambda_{1} & & & \\ & \lambda_{2} & & \\ & & \ddots & \\ & & & \lambda_{n} \end{array}\right]\left[\begin{array}{c} \mathbf{q}_{1}^{\mathrm{T}} \\ \mathbf{q}_{2}^{\mathrm{T}} \\ \vdots \\ \mathbf{q}_{n}^{\mathrm{T}} \end{array}\right] \\ &=\lambda_{1} \mathbf{q}_{1} \mathbf{q}_{1}^{\mathrm{T}}+\lambda_{2} \mathbf{q}_{2} \mathbf{q}_{2}^{\mathrm{T}}+\ldots+\lambda_{n} \mathbf{q}_{n} \mathbf{q}_{n}^{\mathrm{T}} \end{aligned}$$如果忘了这个这么计算的，可以看一下前面提到的一个例子$$\left[\begin{array}{ll} 1 & 4 \\ 1 & 5 \end{array}\right]\left[\begin{array}{ll} 3 & 2 \\ 1 & 0 \end{array}\right]=\left[\begin{array}{ll} 1 \\ 1 \end{array}\right]\left[\begin{array}{ll} 3 & 2 \end{array}\right]+\left[\begin{array}{l} 4 \\ 5 \end{array}\right]\left[\begin{array}{ll} 1 & 0 \end{array}\right]=\left[\begin{array}{ll} 3 & 2 \\ 3 & 2 \end{array}\right]+\left[\begin{array}{ll} 4 & 0 \\ 5 & 0 \end{array}\right]$$ 相乘的两个矩阵分别切割成列向量和行向量然后再加和。矩阵\( \mathbf{q}_{\mathbf{k}} \mathbf{q}_{\mathbf{k}}^{\mathrm{T}}\left(=\mathbf{q}_{\mathbf{k}} \mathbf{q}_{\mathbf{k}}^{\mathrm{T}} /\left(\mathbf{q}_{\mathbf{k}}^{\mathrm{T}} \mathbf{q}_{\mathbf{k}}\right)\right)\)是朝向\( \mathbf{q}_\mathbf{k}\)的投影矩阵(模长是\(1 \)，省略了)，所以每一个矩阵都是正交投影矩阵的线性组合，线性组合的系数就是对应的特征值。这是理解谱定理的另一种方法。
对称矩阵的特征值的正负性质
我们先前已经知道，对于实对称阵，它的特征值一定是实数，那么下一步我们要思考特征值的正负号问题，正如我们先前讨论微分方程的例子，特征值的正负号影响着系统的稳定性。但是对于大型矩阵，通过计算\(|\boldsymbol{A}-\lambda \boldsymbol{I}|=0 \)得到特征值进行判定理论上可行，但是计算量很大，即使用matlab求解，结果也不一定可靠，但matlab可以得到矩阵的主元，而对称矩阵的主元中正负号的个数与特征值相同，即正主元的数目等于正特征值的数目。具体证明见pdf的资料。
矩阵\( \boldsymbol{A}+\mathbf{b} \boldsymbol{I}\)的特征值比矩阵\(\boldsymbol{A}\)的特征值大\( \mathbf{b} \)。利用此性质可以估计特征值的状态。
【正定矩阵】(Positive definite matrices)
正定矩阵是对称矩阵的子集，就是所有特征值都是正数的对称矩阵。对一个对称矩阵来说，所有的主元都是正数和所有的特征值都是正数，这两个描述的是等价的。特征值都是正数，那么零肯定不是特征值，于是矩阵的行列式不等于零，就是一个满秩矩阵，而主元都是正数，因此矩阵的行列式一定也是正数。行列式为正数，不代表所有特征值都是正数。
若将行列式作为正定的判据，则要求\(n \)阶矩阵左上角的所有方子矩阵行列式数值均为正数，矩阵才能确定为正定矩阵。
谱定理(主轴定理)
Linear.1 谱定理(Spectral Theorem )通往PCA和SVD的基石.(T-B)
xx
什么是椭球和双曲面的主轴？
主轴定理：
补充
Linear.1 谱定理（Spectral Theorem ）通往PCA和SVD的基石.(T-B)
复矩阵和FFT
复矩阵
【复向量】(Complex vectors)，我们先前讨论的都向量或者矩阵都是属于\(\mathbf{R}^{n} \)空间，其中的 \(\mathbf{R}\)表示的是实数。实数矩阵可能出现复数特征值的情况，由于接下来我们将讨论复数矩阵，于是必须了解复数向量相关的知识。对于复数向量或者复数矩阵，这个时候就是属于\(\mathbf{C}^{n} \)空间了，而不是实数空间。
模长方：对于给定的复向量\( \mathbf{z}\in \mathbf{C}^{n}\)，\( \mathbf{z}^{\mathrm{T}} \mathbf{z}\)不给出其模长的平方，比如\( \left[\begin{array}{ll} 1 & i \end{array}\right]\left[\begin{array}{l} 1 \\ i \end{array}\right]=0\)。定义复向量向量模长的平方为$$|\mathbf{z}|^{2}=\overline{\mathbf{z}}^{\mathrm{T}}\mathbf{z}=\left|\mathbf{z}_{1}\right|^{2}+\left|\mathbf{z}_{2}\right|^{2}+\cdots+\left|\mathbf{z}_{n}\right|^{2}$$于是\( \left[\begin{array}{l} 1 \\ i \end{array}\right]\)模长方就是\([1-i]\left[\begin{array}{l} 1 \\ i \end{array}\right]=2 \)。记\( |\mathbf{z}|^{2}=\bar{\mathbf{z}}^{\mathrm{T}} \mathbf{z}=\mathbf{z}^{\mathrm{H}} \mathbf{z}\)，其中的\(\mathrm{H}\)来自Hermite(厄米特)。
内积：类似地，内积的定义变成\(\mathbf{y}^{\mathrm{H}} \mathbf{x}=\overline{\mathbf{y}}^{\mathrm{T}} \mathbf{x}=\overline{\mathbf{y}}_{1} \mathbf{x}_{1}+\overline{\mathbf{y}}_{2} \mathbf{x}_{2}+\cdots+\overline{\mathbf{y}}_{n} \mathbf{x}_{n} \)，注意这里得到的内积很可能不是实数，而是复数，只有当\( \mathbf{x}=\mathbf{y}\)时结果才是实数。
【复矩阵】(Complex matrices)，前面我们讨论过实对称阵的特征值都是实数，而对于复对称阵来说，只有满足\( \overline{\boldsymbol{A}}^{\mathrm{T}}=\boldsymbol{A}\)的矩阵的特征值才是实数，满足这样条件的复矩阵成为【厄米特矩阵】(Hermitian matrixes)。对一个复数矩阵进行共轭+转置操作可以用\(\mathrm{H}\)作为上标，即\( A^{\mathrm{H}}=\bar{A}^{\mathrm{T}}\)。例如厄米特矩阵\( \left[\begin{array}{cc} 2 & 3+i \\ 3-i & 5 \end{array}\right]\)具有实数特征值和正交的特征向量(任意厄米特矩阵均成立)。显然厄米特矩阵的主对角线上的元素必须都是实数。
【酉矩阵】(unitary matrix)：复空间的标准正交矩阵称。对于\(\mathbf{C}^{n} \)空间的标准正交基\( \mathbf{q}_{1}, \mathbf{q}_{2},\cdot\cdot \cdot\cdot\cdot ,\mathbf{q}_{n}\)有\(\overline{\mathbf{q}}_{\mathbf{j}}^{\mathrm{T}} \mathbf{q}_{\mathbf{k}}=\left\{\begin{array}{ll} 0 & j \neq k \\ 1 & j=k \end{array}\right. \)。用这些复向量作为列向量可以构造出的矩阵\(Q \)为酉矩阵，即有\(\overline{Q}^{\mathrm{T}}Q=I=Q^{\mathrm{H}} Q \)。
快速傅里叶变换(FFT)
傅里叶级数是将周期韩硕或者信号变换为不同频率的三角函数的和函数。$$f(x)=a_{0}+a_{1} \cos x+b_{1} \sin x+a_{2} \cos 2 x+b_{2} \sin 2 x+\cdots$$在电子工程或者计算机科学中，\( n \times n\)矩阵的行和列从第\( 0\)行和第\(0 \)列开始计数，最后到第\((n-1)\)行和第\((n-1)\)列。我们在讨论【离散傅里叶变换矩阵】(DFT matrix)的时候遵从这种习惯。$$F_{n}=\frac{1}{\sqrt{n}}\left[\begin{array}{ccccc} 1 & 1 & 1 & \cdots & 1 \\ 1 & \omega & \omega^{2} & & \omega^{(n-1)} \\ 1 & \omega^{2} & \omega^{4} & & \omega^{2(n-1)} \\ \vdots & & & \ddots & \\ 1 & \omega^{n-1} & \omega^{2(n-1)} & & \omega^{(n-1)^{2}} \end{array}\right]$$ \(\left(F_{n}\right)_{jk}=\omega^{jk} \)，傅里叶矩阵为对称阵\( F_{n}=F_{n}^{\mathrm{T}}\)，其中的\(\omega=\exp (i 2 \pi / n) \)，于是\( \omega^{n}=1\)。矩阵的列向量正交，\(\omega \)的次方分布在复平面的单位圆上，只是幅角不同。当\( n=4\)时，\(\omega^{4}=1, \omega=\exp (i 2 \pi / 4)=i \)。$$F_{4}=\frac {1 }{ 2} \left[\begin{array}{llll} 1 & 1 & 1 & 1 \\ 1 & i & i^{2} & i^{3} \\ 1 & i^{2} & i^{4} & i^{6} \\ 1 & i^{3} & i^{6} & i^{9} \end{array}\right]=\frac {1 }{ 2} \left[\begin{array}{rrrr} 1 & 1 & 1 & 1 \\ 1 & i & -1 & -i \\ 1 & -1 & 1 & -1 \\ 1 & -i & -1 & i \end{array}\right]$$傅里叶矩阵特点分析：
- 正交性：列向量相互垂直，注意计算的时候要对其中的一个复向量取共轭；
- 归一性：显然列向量长度乘以矩阵外的系数，都为\(1\)；
- 逆矩阵：就像实数域的标准正交矩阵的逆矩阵为其转置一样，复数域的酉矩阵的逆矩阵为其共轭转置矩阵，\( F_{4}^{\mathrm{H}} F_{4}=I\)。
- \(F_{4}\)为一个四点傅里叶变换(离散的)矩阵矩阵，\(F_{4}\mathbf{x}\)表示对一个一个四维列向量做离散傅里叶变换，\(\mathbf{x}F_{4}^{-1}\)表示对一个一个四维列向量做离散的傅里叶逆变换。
- DFT matrix还有一个特别之处在于，类似前面的各种矩阵分解方法，我们也可以将其分解为含有【稀疏矩阵】的表达式，见下面。
- \(F_{6}\)和\(F_{6}\)之间存在某种奇妙的联系，\(F_{8}\)和\(F_{4}\)之间存在某种奇妙的联系，\(F_{64}\)和\(F_{32}\)之间存在某种奇妙的联系。这种联系可以通过矩阵的分解表现出来，见下面的讨论。
稀疏矩阵：在数值分析中，是其元素大部分为零的矩阵。反之，如果大部分元素都非零，则这个矩阵是稠密(dense)的。在科学与工程领域中求解线性模型时经常出现大型的稀疏矩阵。
(1) 为什么大量的问题可以用稀疏矩阵表示？—知乎
(2) 稀疏矩阵的概念介绍—知乎
\( 64\)阶傅里叶矩阵中的\(F_{64} \)与\( 32\)阶傅里叶矩阵\(F_{32} \)的元素\( \omega _{32}\)相比，幅角是其一版，\( (\omega _{64})^{2}=\omega _{32}\)。可以从分块矩阵运算找到两者的联系：$$ \left[{F}_{64}\right]=\left[\begin{array}{cc} {I} & {D} \\ {I} & {D} \end{array}\right]\left[\begin{array}{cc} {F}_{32} & \mathbf{0} \\ \mathbf{0} & {F}_{32} \end{array}\right]\left[\begin{array}{l} \text { permutation } \end{array}\right] $$其中最后侧的矩阵为置换矩阵，其作用是让奇数行的元素排在前面，然后再排偶数行的元素，注意这里第一行的元素是\(x_0\)。重排矩阵(对角阵)$$ D=\left[\begin{array}{lllll} 1 & & & & \\ & \omega & & & \\ & & \omega^{2} & & \\ & & & \ddots & \\ & & & & \omega^{31} \end{array}\right] $$复习一下置换矩阵，下面这个矩阵作用在列向量，就是将其奇数列的元素提前。
计算开销估算：
- 如果是\(F_{64}\)作用在一个\(64\)维列向量上，那么在忽略加法计算的情况下，矩阵中的每一个元素都要做一次乘法运算，于是最终合计要进行\(64^2\)次运算；
- 如果是分解后的矩阵，那么首先置换矩阵的效果可以在瞬间完成，可忽略其计算量，对于中间的矩阵，相当于重复两次\(F_{32}\)作用在一个\(32\)维列向量上，所消耗的计算量为\(2\times 32^2\)，修正矩阵增加的计算量主要由对角阵\( D\)贡献，一共是\(32\)次乘法。汇总一下，总的计算量为\( 2\times 32^2+32\)；
- 继续进行分解，不断进行下去，最终的状态是，计算量为\(\displaystyle\frac{1}{2} n \log _{2} n\)。假设\( n=1024=2^{10}\)，那么计算量减少为原来的大约\( 1/200\)，非常显著。
上图来自DFT matrix—Wiki，有空的话，补充一下自己的理解。
DFT中的特征值/向量
补充
FFT得到的结果是symmtetric(mirror relationship)，所以我们只需要截取前一半即可。
参考资料：
(1) 如何通俗地理解傅立叶变换?—马同学
(2) 傅里叶变换的矩阵分析—CSDN
(3) DFT matrix—Wiki
正定矩阵和最小值
先前我们学习了所有特征值都是正数的对称矩阵是正定矩阵，正定矩阵将主元、行列式、特征值以及方程的稳定性融为一体。这里讲介绍如何判断一个矩阵是不是正定矩阵，以及当一个矩阵是正定矩阵时，其内涵和矩阵操作的效果有何特别之处。此外还有特定矩阵与几何的关系：椭圆和正定有关，双曲线与正定无关。
对于一个二阶对称阵\(\left[\begin{array}{ll} a & b \\ b & c \end{array}\right] \)，可以从四个角度来判定是否是【正定矩阵】。
(1) 特征值\( \lambda_{1}>0, \lambda_{2}>0\)；
(2) 行列式(所有子行列式)\( a>0, a c-b^{2}>0\)；
(3) 主元(消元之后)\(a>0,\left(a c-b^{2}\right) / a>0 \)；
(4) 表达式\(\mathbf{x}^{\mathrm{T}} \boldsymbol{A} \mathbf{x}>0 \)(\(\mathbf{x}=0 \)除外)。这就是正定的定义，而前面三条是用来验证正定性的条件。
给定矩阵\(A=\left[\begin{array}{ll} 2 & 6 \\ 6 & y \end{array}\right] \)正定的条件是\(2 y-36>0 \)，即\( y>18\)。
矩阵\( \left[\begin{array}{cc} 2 & 6 \\ 6 & 18 \end{array}\right]\)正好处在判定正定矩阵的临界点上，所以称之为半正定(positive semidefinite)矩阵，由于行列式等于零，因此具有一个特征值\( 0\)，是奇异矩阵，只有一个主元。半正定矩阵特征值大于等于零。
再来研究第四条判据，以二阶对称矩阵为例子$$ \mathbf{x}^{\mathrm{T}} \boldsymbol{A} \mathbf{x}=\left[\begin{array}{ll} x_{1} & x_{2} \end{array}\right]\left[\begin{array}{cc} 2 & 6 \\ 6 & 18 \end{array}\right]\left[\begin{array}{l} x_{1} \\ x_{2} \end{array}\right]=2 x_{1}^{2}+12 x_{1} x_{2}+18 x_{2}^{2} $$这种操作最终得到的是一个多项式，而且每一项都是未知元素的二次，因此叫作【二次型】。如果对于任意\(x \)和\( y\)，这种二次型(quadratic form)\( a x^{2}+2 b x y+c y^{2}\)均大于零，则矩阵为正定矩阵。对于我们前面提到的半正定矩阵来说，只存在唯一一组\( x_{1}=3, x_{2}=-1\)，使得\( 2 x_{1}^{2}+12 x_{1} x_{2}+18 x_{2}^{2}=2\left(x_{1}+3 x_{2}\right)^{2}=0\)。
正定矩阵和最小二乘法
正定矩阵有助于数值计算。对于正定矩阵，不需要进行行交换，也不必担心主元过小或者等于零，它们是容易计算的矩阵(great matrices)。我们先回忆一下最小二乘法，原始方程为\( \boldsymbol{A}^{\mathrm{T}}(\mathbf{b}-\boldsymbol{A} \hat{\mathbf{x}}) =0\)(回忆一下等式的由来特别是正交关系)，移到两边有\( \boldsymbol{A}^{\mathrm{T}} \boldsymbol{A} \hat{\mathbf{x}}=\boldsymbol{A}^{\mathrm{T}} \mathbf{b}\)。我们知道原始数据的系数矩阵是\(\boldsymbol{A} \)，这里的\(\boldsymbol{A}\)很大概率不是方阵，也就是说方程的个数大于未知数的个数，而转换后的矩阵\( \boldsymbol{A}^{\mathrm{T}} \boldsymbol{A} \)是一个方阵，换句话说未知数的个数(最优解)就和方程的个数相等了。那么这个\(\boldsymbol{A}^{\mathrm{T}} \boldsymbol{A} \)是否是正定矩阵呢？
对其两边取转置等于自己，所以必然是对称阵(正定矩阵属于对称阵中一类)，利用我们先前对正定矩阵的判据(4)，我们有\(\boldsymbol{x}^{\mathrm{T}}\left(\boldsymbol{A}^{\mathrm{T}} \boldsymbol{A}\right) \mathbf{x}=(\boldsymbol{A} \mathbf{x})^{\mathrm{T}}(\boldsymbol{A} \mathbf{x})=|\boldsymbol{A} \mathbf{x}|^{2} \geq 0 \)因此\( \)。当且仅当\(\boldsymbol{A} \mathbf{x}=0 \)时，表达式为\( 0\)。当矩阵\(\boldsymbol{A} \)的各列线性无关时，矩阵为列满秩\(r=n \)，\(\boldsymbol{A} \)的零空间只有零向量，那么在这个条件下前面的不等式才取等号。因此如果\( \boldsymbol{A}\)是列满秩矩阵，那么\(\boldsymbol{A}^{\mathrm{T}} \boldsymbol{A} \)一定是正定矩阵。
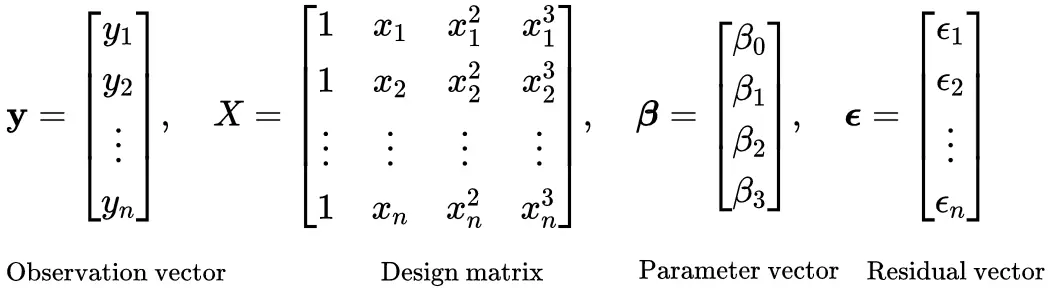
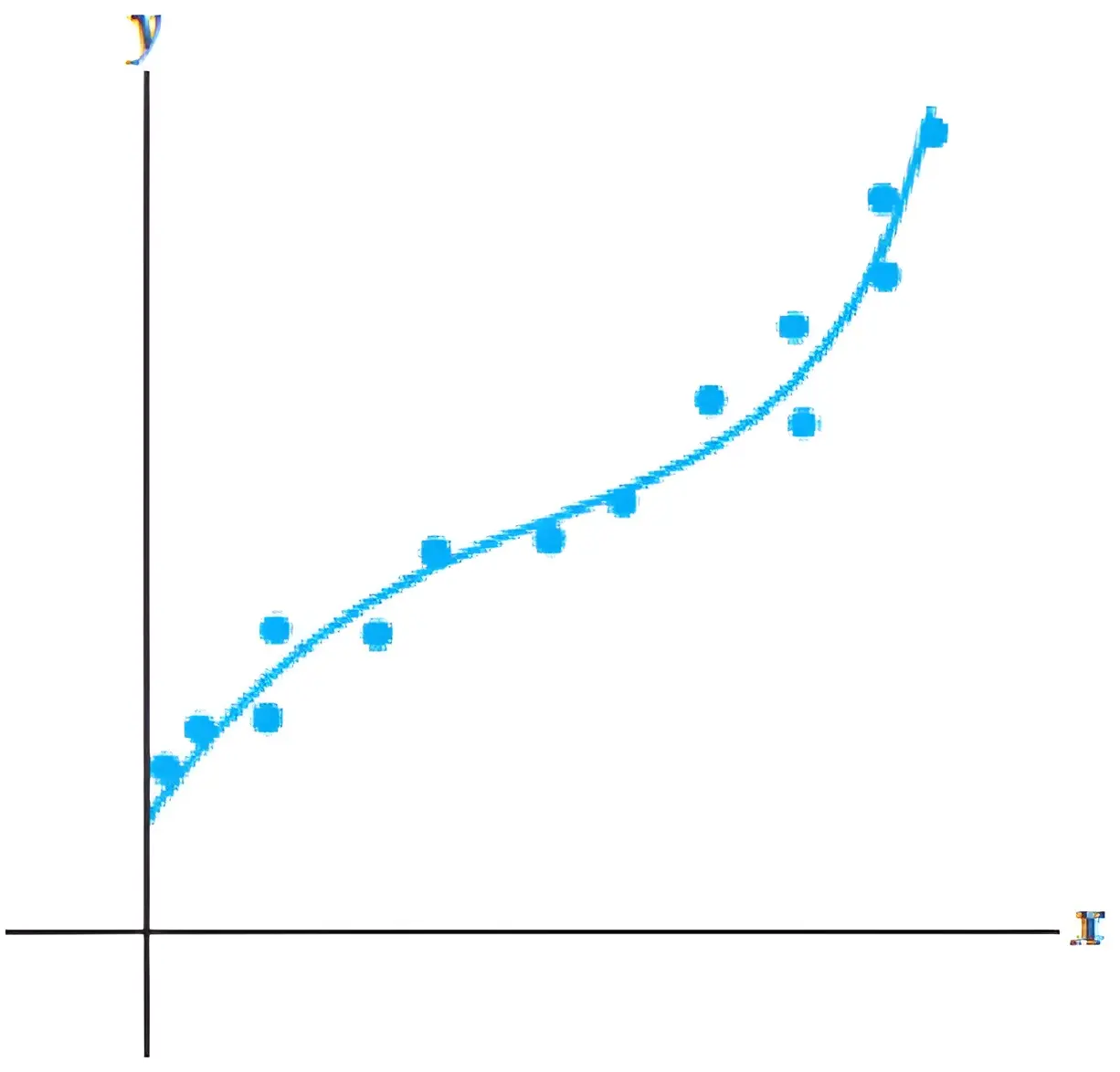说到了 \(\boldsymbol{A}^{\mathrm{T}} \boldsymbol{A}\) 和最小二乘问题就要解释一下，GS 举得曲线拟合的例子，都是线性公式 \(y=a x+b\)，但实际上最小二乘法也处理非线性方程，因为这里所谓的非线性 是对\(x\)而言，而只要对于所求的参数是线性方程就可以。比如下面的例子中 \(x\) 的方幂组成的矩阵\(X\)只是一个系数矩阵，对于所求的参数这仍是个线性方程组。
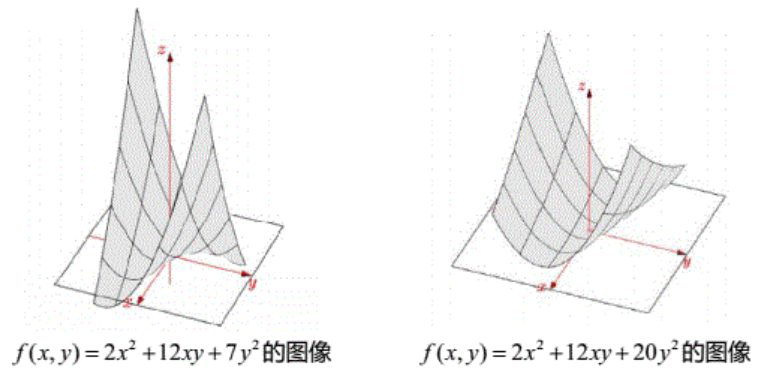
二次型的函数图像分析(可以借助CalcPlot3D 和Desmos 画图工具)
(1) 非正定矩阵\(\left[\begin{array}{ll} 2 & 6 \\ 6 & 7 \end{array}\right] \)，二次型为\(f(x, y)=2 x^{2}+12 x y+7 y^{2} \)。从几何图像上看没有最小值点，在原点处有一鞍点。鞍点在某个方向上看是极大值点，在另一个方向上看是极小值点，实际上最佳观测角度是特征向量的方向。
(2) 正定矩阵\( \left[\begin{array}{cc} 2 & 6 \\ 6 & 20 \end{array}\right]\)，二次型为\( f(x, y)=2 x^{2}+12 x y+20 y^{2}\)，在原点的一阶偏导数为零，二阶偏导数大于零，是最小值点。
思考一下，对于半正定矩阵，函数图像应该是怎么样的，比如对于我们前面提到的\( \left[\begin{array}{cc} 2 & 6 \\ 6 & 18 \end{array}\right]\)，二次型为\( 2\left(x_{1}+3 x_{2}\right)^{2}\)，于是在\(x_{1}+3 x_{2}=0 \)这条过原点的直线就是函数的“最小线”，整条直线上对应的函数值\( 0\)都是整个函数图像上的最小值，类似将一张A4纸沿着中间线弯曲。
二次型与配方法
对于上一个问题的例子(2)根绝配方法可以写成\(f(x, y)=2 x^{2}+12 x y+20 y^{2}=2(x+3 y)^{2}+2 y^{2} \)，前面的\( x^{2}\)和\( x y\)项完成配方以后，如果有多出来的\( y^{2}\)项，那么原矩阵就是正定的，正好没有多的，那就是半正定，如果还要减去\( y^{2} \)项，那么就是非正定矩阵。这里有多余的\( y^{2}\)项，因此就是正定矩阵，其集合图像为碗型的曲面，如果用\(z=1 \)进行截面切割，相交得到的就是\( 2(x+3 y)^{2}+2 y^{2}=1\)椭圆曲线。而对双曲面进行切割就得到双曲线？？？。
注意，椭圆\( 2(x+3 y)^{2}+2 y^{2}=1\)相当于对我们接触的正着放着的椭圆进行了一定的旋转操作，还有对应轴的伸缩操作，但最终得到的仍旧是一个椭圆，相当于对原来的\(\left[\begin{array}{l} x \\ y \end{array}\right] \)向量左乘了一个矩阵。
待整理
【黑塞矩阵】
设有一实函数\(f\left(x_{1}, x_{2}, \ldots, x_{n}\right) \)，如果函数\( f\)的所有二阶偏导数都存在并且在定义域内连续，那么函数\( f\)的黑塞矩阵为$$\mathbf{H}=\left[\begin{array}{cccc} \displaystyle\frac{\partial^{2} f}{\partial x_{1}^{2}} & \displaystyle\frac{\partial^{2} f}{\partial x_{1} \partial x_{2}} & \cdots & \displaystyle\frac{\partial^{2} f}{\partial x_{1} \partial x_{n}} \\ \displaystyle\frac{\partial^{2} f}{\partial x_{2} \partial x_{1}} & \displaystyle\frac{\partial^{2} f}{\partial x_{2}^{2}} & \cdots & \displaystyle\frac{\partial^{2} f}{\partial x_{2} \partial x_{n}} \\ \vdots & \vdots & \ddots & \vdots \\ \displaystyle\frac{\partial^{2} f}{\partial x_{n} \partial x_{1}} & \displaystyle\frac{\partial^{2} f}{\partial x_{n} \partial x_{2}} & \cdots & \displaystyle\frac{\partial^{2} f}{\partial x_{n}^{2}} \end{array}\right]$$可以简写为$$\mathbf{H}_{i, j}=\frac{\partial^{2} f}{\partial x_{i} \partial x_{j}}$$该函数若在\( x_{0}\left(x_{1}, x_{2}, \cdots, x_{n}\right) \)处取的极值，那么极值存在的必要条件为$$\nabla f\left(x_{0}\right)=\left[\begin{array}{llll} \displaystyle\frac{\partial f}{\partial x_{1}} & \displaystyle\frac{\partial f}{\partial x_{2}} & \cdots & \displaystyle\frac{\partial f}{\partial x_{n}} \end{array}\right]_{x_{0}}^{T}=0$$取得极小值的充分条件为上述黑塞矩阵正定，取得极大值的充分条件为上述黑塞矩阵负定。回想一下一元函数求极大值/极小值的判定方法，这里不过是给出了多元函数极值点的判定方法。
顺便说一下【雅各比矩阵】：球坐标系$$\begin{array}{l} x=r \sin \theta \cos \varphi \\ y=r \sin \theta \sin \varphi \\ z=r \cos \theta \end{array}$$其雅各比矩阵为$$\mathbf{J}_{\mathbf{F}}(r, \theta, \varphi)=\left[\begin{array}{ccc} \displaystyle\frac{\partial x}{\partial r} & \displaystyle\frac{\partial x}{\partial \theta} & \displaystyle\frac{\partial x}{\partial \varphi} \\ \displaystyle\frac{\partial y}{\partial r} & \displaystyle\frac{\partial y}{\partial \theta} & \displaystyle\frac{\partial y}{\partial \varphi} \\ \displaystyle\frac{\partial z}{\partial r} & \displaystyle\frac{\partial z}{\partial \theta} & \displaystyle\frac{\partial z}{\partial \varphi} \end{array}\right]$$雅各比行列式的值为\( r^{2} \sin \theta\)，那么\( d V=d x d y dz=r^{2} \sin \theta d r d \theta d \varphi \)就很自然了。
拓展资料：
(1) Jacobian矩阵和Hessian矩阵的作用是什么?—知乎
(2) 理解Jacobian和Hessian—知乎