角动量

自旋角动量与轨道角动量的物理意义？
量子力学中轨道角动量怎么定义？是r×p吗？但是r和p不能同时确定吧？

回顾：主量子数\( n \)确定的是能量，而\( l \)和\(m \)与角动量有关。

经典物理上，一个粒子的角动量为\(  \mathbf{L}=\mathbf{r} \times \mathbf{p}\)，分量形式为(根据向量叉乘的法则)$$L_{x}=y p_{z}-z p_{y}, L_{y}=z p_{x}-x p_{z}, L_{z}=x p_{y}-y p_{x}$$对应的算符为$$p_{x} \rightarrow-i \hbar \partial / \partial x, \quad p_{y} \rightarrow-i \hbar \partial / \partial y, \quad p_{z} \rightarrow-i \hbar \partial / \partial z$$

量子力学中算符满足$$\begin{aligned} &[A, B+C]=[A, B]+[A, C]\\ &[A B, C]=A[B, C]+[A, C] B \end{aligned}$$

本征值

先证明\(L_x  \)、\(L_y  \)和\(L_z  \)之间任意两个都不对易，只需证明一个即可。$$\begin{aligned} \left[L_{x}, L_{y}\right] &=\left[y p_{z}-z p_{y}, z p_{x}-x p_{z}\right] \\ &=\left[y p_{z}, z p_{x}\right]-\left[y p_{z}, x p_{z}\right]-\left[z p_{y}, z p_{x}\right]+\left[z p_{y}, x p_{z}\right] \end{aligned}$$注意\( p_{z} \)和\( z \)是不对易的，其他也类似。对于对易的项目(\(\left[y , p_{x}\right]  \))，我们直接提出来，比如\( \left[y p_{z}, z p_{x}\right] \)中直接将\( y p_{x} \)提出来。因此$$\left[L_{x}, L_{y}\right]=y p_{x}\left[p_{z}, z\right]+x p_{y}\left[z, p_{z}\right]=i \hbar\left(x p_{y}-y p_{x}\right)=i \hbar L_{z}$$于是得证$$\left[L_{x}, L_{y}\right]=i \hbar L_{z} ; \quad\left[L_{y}, L_{z}\right]=i \hbar L_{x} ; \quad\left[L_{z}, L_{x}\right]=i \hbar L_{y}$$\(L_x  \)、\(L_y  \)和\(L_z  \)之间任意两个都不对易说明不能同时准确测量其中任意两个(本征值)，也就是存在测不准原理。或者说任意两个都不具有相同的本征函数。

下面我们证明角动量的平方\(  L^{2}=L_{x}^{2}+L_{y}^{2}+L_{z}^{2}\)和三个分量之间存在对易关系。$$\begin{aligned} \left[L^{2}, L_{x}\right] &=\left[L_{x}^{2}, L_{x}\right]+\left[L_{y}^{2}, L_{x}\right]+\left[L_{z}^{2}, L_{x}\right] \\ &=L_{y}\left[L_{y}, L_{x}\right]+\left[L_{y}, L_{x}\right] L_{y}+L_{z}\left[L_{z}, L_{x}\right]+\left[L_{y}, L_{x}\right] L_{z} \\ &=L_{y}\left(-i \hbar L_{z}\right)+\left(-i \hbar L_{z}\right) L_{y}+L_{z}\left(i \hbar L_{y}\right)+\left(i \hbar L_{y}\right) L_{z} \\ &=0 \end{aligned}$$于是证实$$\left[L^{2}, L_{x}\right]=0, \quad\left[L^{2}, L_{y}\right]=0, \quad\left[L^{2}, L_{z}\right]=0$$\(  L^{2}\)和\( L_{z} \)对易，说明我们可以找到\( L^2 \)和\(L_{z}  \)二者共同的本征态，但是特征值不同(显然不同，量纲分析都知道两个特征值的单位不同，另外\( L \)的单位其实和\(\hbar  \)一样，我们后面会知道\(  L = \sqrt{(l(l+1))}\hbar\))$$\left\{\begin{array}{l} L^{2} f=\lambda f \\ L_{z} f=\mu f \end{array}\right.$$同样采用“梯子算符”的方法，令$$L_{\pm} \equiv L_{x} \pm i L_{y}$$注：虽然我们讨论的\(  L_x\)、\(  L_y\)、\(  L_z\)和\( L \)以及\( L^2 \)都是可观测量，也就都是厄米算符作用得到的；但是这里的\( L_{\pm} \)梯子算符不一定是厄米算符，那么特征值不一定是实数。

(1)  \(\left[L^{2}, L_{\pm}\right]=0  \)
因为\( L_{\pm} \)是由\(  L_{x}\)和\( L_{y} \)线性组合得到，而它们各自与\(  L^{2}\)对易。
(2)  \(\left[L_{z}, L_{\pm}\right]=\pm \hbar L_{\pm}  \)，即$$\left\{\begin{array}{l} {\left[L_{z}, \quad L_{+}\right]=\hbar L_{+}} \\ {\left[L_{z},\quad L_{-}\right]=-\hbar L_-} \end{array}\right.$$证明如下：
\( \left[L_{z}, L_{\pm}\right]=\left[L_{z}, L_{x}\right] \pm i\left[L_{z}, L_{y}\right]=i \hbar L_{y} \pm i\left(-i \hbar L_{x}\right)=\pm \hbar\left(L_{x} \pm i L_{y}\right) \)

阶梯讨论

先前我们说，\(  f\)同时是\(  L^{2}\)和\( L_{z} \)的本征函数，那么如果用阶梯算符作用在本征函数上，即\( L_{\pm} f \)，它依旧是\(  L^{2}\)和\( L_{z} \)的本征函数吗？如果是，那么本征值如何变化？

(1) \( L_{\pm} f \)同样是\(  L^{2}\)的本征函数，而且本征值不变，依然为\(\lambda  \) $$L^{2}\left(L_{\pm} f\right)=L_{\pm}\left(L^{2} f\right)=L_{\pm}(\lambda f)=\lambda\left(L_{\pm} f\right)$$(2) \( L_{\pm} f \)同样是\( L_{z} \)的本征函数，但是本征值由\( \mu \)  变为\( (\mu \pm \hbar) \)。$$\begin{aligned} L_{z}\left(L_{\pm} f\right) &=\left(L_{z} L_{\pm}-L_{\pm} L_{z}\right) f+L_{\pm} L_{z} f=\pm \hbar L_{\pm} f+L_{\pm}(\mu f) \\ &=(\mu \pm \hbar)\left(L_{\pm} f\right) \end{aligned}$$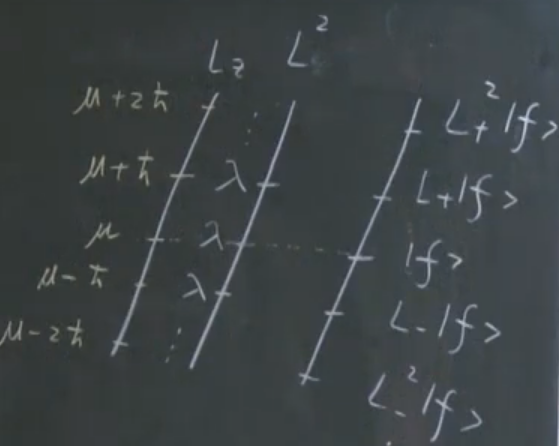形象理解(一个固定长度的臂，在支点上下转动；臂长是固定的，对应的特征值\(  \lambda\)就不变，但是投影到\(  z\)方向的\( L_z \)在不断变化，而且是只能在特定角度变化，让\(L_z   \)的特征值量子化)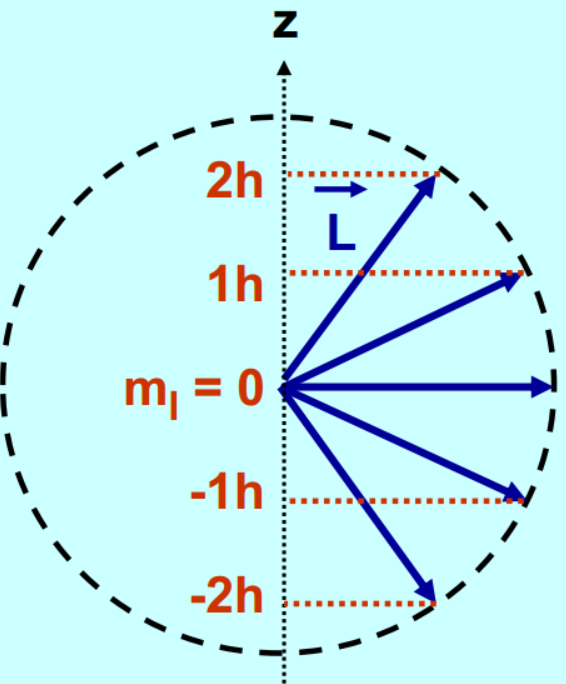注：因为实际上三个方向的角动量是不互易的，所以实际上不可能同时准确量测，因此\(  L\)存在一定的不确定性(模糊的地方，如果不模糊，说明知道三个方向的分量，矛盾)，也就是说上图不准确，但是便于我们形象理解。

限定条件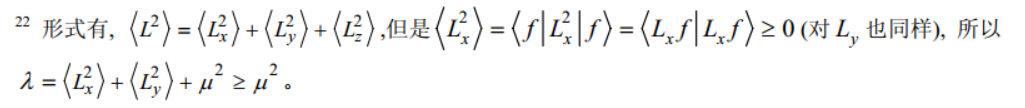：每作用一个升阶算符，\(\mu  \)就会增加\( \hbar \)，显然不可能无限制升，否则\(  \mu^{2}\)就会大于\( \lambda \)，那么\(  x\)和\(  y\)方向的角动量平方为负值，显然不可能。同样的道理，也不能无限制下降。因此必然存在最高阶梯\( f_{t} \)和最低阶梯\( f_{b} \)，使得$$\left\{\begin{array}{l} L_+\left|f_{t}\right\rangle=0 \\ L_{-}\left|f_{b}\right\rangle=0 \end{array}\right.$$不然上下无限延伸，分量的能量反而大于总的能量，显然不可能。

回顾一下前面的知识$$\begin{array}{l} {\left[L_{x}, L_{y}\right]=i \hbar L_{z} \quad\left[L^{2}, \mathbf{L}\right]=0} \\ {\left[L_{y} \cdot L_{z}\right]=i \hbar L_{x}} \\ {\left[L_{z}, L_{x}\right]=i \hbar L_{y} \quad\left\{\begin{array}{l} L^{2} f=\lambda f \\ L_{z} f=\mu f \end{array}\right.} \\ L^{2}=L_{x}^{2}+L_{y}^{2}+L_{z}^{2} \\ L_{\pm}=L_{x} \pm i L_{y} \end{array}$$
我们现在有$$\left\{\begin{array}{l} L_z f_{t}=\alpha f_{t} \\ L^{2} f_{t}=\lambda f_{t} \\ L^{2}=L_{x}^{2}+L_{y}^{2}+L_{z}^{2} \end{array}\right.$$(1)  求最高阶梯
我们要做的是凑出\( L_{+}\left|f_{t}\right\rangle=0 \)，也就是让\( L_{+}  \)作用到\(  f\)上。这里的\(  L_{x}^{2}+L_{y}^{2}\)可以用阶梯算符来表示，从而凑出\( L_{+}\left|f_{t}\right\rangle \)。$$\begin{aligned} L_{-} L_{+} &=\left(L_{x}-i L_{y}\right)\left(L_{x}+i L_{y}\right) \\ &=L_{x}^{2}+L_{y}^{2}+i\left(L_{x} L_{y}-L_{y} L_{x}\right) \\ L_{x}^2+L_{y}^{2}&=L_{-}L_{+}-i \cdot(i \hbar) L_{z} \\ &=L_{-}L_{+} +\hbar L_{z} \end{aligned}$$因此$$L^{2}=L_{x}^{2}+L_{y}^{2}+L_{z}^{2}=L_{-}L_{+}+\hbar L_{z}+L_{z}^{2}$$于是改写下式，凑出了我们要的$$L^{2} f_{t}=\lambda f_{t} \quad \Rightarrow\left(L_{-} L_{+}+\hbar L_{z}+L_{z}^{2}\right) f_{t}=\lambda f_{t}$$因此得到最后的结论$$\alpha \hbar+\alpha^{2}=\lambda$$(2)  求最低阶梯$$\left\{\begin{array}{l} L_{z} f_{b}=\beta f_{b} \\ L^{2} f_{b}=\lambda f_{b} \\ \left(L_{+} L_{-}-\hbar L_{z}+L_{z}^{2}\right) f_{b}=\lambda f_{b} \end{array}\right.$$ 得到最终结果\(- \beta \hbar+\beta^{2}=\lambda  \)
(3)  将(1)和(2)中得到的最终等式合并，得到$$-\beta \hbar+\beta^{2}=\alpha \hbar+\alpha^{2}$$即\((\alpha+\beta)(\alpha-\beta+\hbar)=0  \)，解一为\( \alpha=-\beta \)，解二为\(  \alpha=\beta-\hbar\)(最高的梯子比最低的还小，不可能，排除这个解)。因此最终解为(还没规定\(l  \)一定是整数)$$\alpha=-\beta \equiv \ell \hbar$$角动量的平方\( L^{2} \)的特征值$$\lambda =l \hbar^{2}+l^{2} \hbar^{2} \\=l(l+1) \hbar^{2}  $$显然对\(  L_z\)来说，最低的本征值为\(-\ell \hbar  \)，最高的本征值为\( \ell \hbar \)，它们之间是通过每次升一个\(  \hbar\)来实现的，假设需要爬\( N \)次(非负整数)，那么必有\(  2l\hbar =N\hbar\)，所以\( l=\displaystyle\frac { N }{ 2 }  \)。于是\( l \)可能的取值为\( l=0, \displaystyle\frac{1}{2}, 1, \displaystyle\frac{3}{2}, 2, \quad \dots\dots \)。不同\(l  \)取值下，\( L_z \)的取值如下$$\begin{aligned} \left\langle f\left|L_{z}\right| f\right\rangle &=0 \quad(l=0) \\ &=\frac{1}{2} \hbar \quad \text{or}-\frac{1}{2} \hbar \quad\left(l=\frac{1}{2}\right) \\ &=+\hbar, \quad 0,\quad-\hbar \quad (l=1) \\ &=\ldots \end{aligned}$$
注：我们在求解氢原子的问题时，\( l \)一定是非负的整数，这样才能保证\( P_{l}(x) \)或\(  P_{l}^{m}(x)\) terminate，而不是无线扩展。因此上面的\(l  \)中的半整数对于氢原子的case来说，是不符合条件的，其他纯非负整数是满足条件的。

\(\left\langle L_{z}^{2}\right\rangle_{\max }=l^{2} \hbar^{2}  \)永远比\( \left\langle L^{2}\right\rangle=l(l+1) \hbar^{2} \)小。也就是说\(  L\)不可能全部投影到\(L_z  \)方向；如果出现这种情况，那么\( L_z =L\)以及\( L_x =0\)和\( L_y =0\)都是确定的，但是它们是不互易的，不能同时准确量测。

我们用\(  m\hbar\)表示\(L_z  \)的所有特征值，即$$L_z|f\rangle=m \hbar|f\rangle$$其中\(m=-l,\, -l+1,\, -l+2,\, \dots \dots , 0,\,1\, 2\dots \dots \,l-1\,，l\)

谐振子模型中，利用阶梯算符虽然可以得到一堆特征向量，但是要注意特征向量线性缩放之后仍旧是特征向量，所以为了满足波函数的归一化条件，我们在保证第一个波函数归一化的条件下，用特定的系数取缩放通过阶梯算符得到的新的特征向量，以保证新得到的\(\psi_{n+1}  \)或者\(  \psi_{n-1}\)也是归一化的，即如下$$a_{+} \psi_{n}=\sqrt{n+1} \psi_{n+1}, \quad a_{-} \psi_{n}=\sqrt{n} \psi_{n-1}$$这里对于氢原子模型，我们采用类似的方法$$L_{\pm} f_{\ell}^{m}=A_{l}^{m} f_{l}^{m \pm 1}$$或者写成$$L_{\pm} |\ell, m\rangle=A_{l}^{m}|\ell, m \pm 1\rangle$$我们现在要求的就是\(  A_{l}^{m}\)，使得当$$\langle\ell, m | \ell, m\rangle=1$$成立，并且$$\langle\ell, \operatorname{m \pm}1| \ell, m \pm 1\rangle=1$$成立时的\(  A_{l}^{m}\)。

注：\(L_{\pm} \equiv L_{x} \pm i L_{y} \)，而且\( L_{\pm} \)和\(L_{\mp}  \)是复共轭的(左矢里面的\( L_- \)提到右矢里面要取复共轭)。$$\left\langle f | L_{\pm} g\right\rangle=\left\langle f | L_{x} g\right\rangle \pm i\left\langle f | L_{y} g\right\rangle=\left\langle L_{x} f | g\right\rangle \pm i\left\langle L_{y} f | g\right\rangle=\left\langle\left(L_{x} \mp i L_{y}\right) f | g\right\rangle=\left\langle L_{\mp} f | g\right\rangle, \text { so }\left(L_{\pm}\right)^{\dagger}=L_{\mp}$$因此$$\begin{aligned} \left\langle L_{\pm} f_{l}^{m} | L_{\pm} f_{l}^{m}\right\rangle &=\left\langle f_{l}^{m} | L_{\mp} L_{\pm} f_{l}^{m}\right\rangle \\ &=\left\langle f_{l}^{m} |\left(L^{2}-L_{z}^{2} \mp \hbar L_{z}\right) f_{l}^{m}\right\rangle=\left\langle f_{l}^{m} |\left[\hbar^{2} l(l+1)-\hbar^{2} m^{2} \mp \hbar^{2} m\right] f_{l}^{m}\right\rangle \\ &=\hbar^{2}[l(l+1)-m(m \pm l)]\left\langle f_{l}^{m} | f_{l}^{m}\right\rangle=\hbar^{2}[l(l+1)-m(m \pm 1)] \\ &=\left\langle L_{\pm} f_{l}^{m} | L_{\pm} f_{l}^{m}\right\rangle=\left\langle A_{l}^{m} f_{l}^{m \pm l} | A_{l}^{m} f_{l}^{m \pm l}\right\rangle=\left|A_{l}^{m}\right|^{2}\left\langle f_{l}^{m \pm 1} | f_{l}^{m \pm 1}\right\rangle=\left|A_{l}^{m}\right|^{2} \end{aligned}$$得到重要结论$$A_{l}^{m}=\hbar \sqrt{l(l+1)-m(m \pm 1)}$$注：当\( m \)取\(  l\)或\( -l \)时，系数\(A_{l}^{m}  \)为零，也就是从阶梯的“上顶部”和“下底部”直接归零。

本征函数

此处差一张图片

前面我们用笛卡尔坐标表示\(L_x  \)、\(L_y  \)和\(L_z  \)，现在我们要用球坐标来表示这三个分量。总的角动量$$\mathbf{L}=(\hbar / i)(\mathbf{r} \times \nabla)$$梯度算符在球坐标中展开$$\nabla=\hat{r} \frac{\partial}{\partial r}+\hat{\theta} \frac{1}{r} \frac{\partial}{\partial \theta}+\hat{\phi} \frac{1}{r \sin \theta} \frac{\partial}{\partial \phi}$$另外\( \mathbf{r}=r \hat{r} \)，所以$$\mathbf{L}=\frac{\hbar}{i}\left[r(\hat{r} \times \hat{r}) \frac{\partial}{\partial r}+(\hat{r} \times \hat{\theta}) \frac{\partial}{\partial \theta}+(\hat{r} \times \hat{\phi}) \frac{1}{\sin \theta} \frac{\partial}{\partial \phi}\right]$$而\(  (\hat{r} \times \hat{r})=0, \quad(\hat{r} \times \hat{\theta})=\hat{\phi}, \quad(\hat{r} \times \hat{\phi})=-\hat{\theta}\)，因此$$\mathbf{L}=\frac{\hbar}{i}\left(\hat{\phi} \frac{\partial}{\partial \theta}-\hat{\theta} \frac{1}{\sin \theta} \frac{\partial}{\partial \phi}\right)$$

自旋

经典力学中，物体的角动量可以分为轨道角动量(公转\( \mathbf{L}=\mathbf{r} \times \mathbf{p} \))和自旋角动量(自转\( \mathbf{S}=I \omega \))。电子围绕原子核旋转运动，也存在轨道角动量和自旋角动量。前者可以和实际物体类比，另外轨道角动量的反方向就是磁矩的方向，而且二者的大小存在一个固定的比例。后者自旋角动量，对电子来说，不能类比实际宏观物理的旋转运动，和经典的自旋无关，只是借用名字，我们只需要知道电子的自旋角动量是电子的内在禀赋(intrinsic property)。每一种基本粒子都有一个特定的永远不变的自旋数。

自旋的代数理论与轨道角动量的极其相似，存在基本对易关系：$$\left[S_{x}, S_{y}\right]=i \hbar S_{z}, \quad\left[S_{y}, S_{z}\right]=i \hbar S_{x}, \quad\left[S_{z}, S_{x}\right]=i \hbar S_{y}$$和前面的类似，也存在$$S^{2}|s, m\rangle= s(s+1)\hbar^{2}|s, m\rangle ; \quad S_{z}|s, m\rangle=m\hbar |s, m\rangle$$以及$$S_{\pm}|s, m\rangle=\hbar \sqrt{s(s+1)-m(m \pm 1)}|s, m \pm 1\rangle$$其中\(  S_{\pm} \equiv S_{x} \pm i S_{y}\)。对于自旋，只能要求是半整数，因此有$$s=0, \frac{1}{2}, 1, \frac{3}{2}, \ldots ; \quad m=-s,-s+1, \ldots, s-1$$规定了电子的自旋\(  s= \displaystyle\frac{1}{2}\)，所以\( m=\displaystyle\frac { 1 }{  2}  \)或\( m=-\displaystyle\frac {  1}{  2}  \)。

注：对于轨道角动量有
\(  L^{2}|l, m\rangle= l(l+1)\hbar^{2}|l, m\rangle ; \quad L_{z}|l, m\rangle=l\hbar |l, m\rangle\)
\(  L_{\pm}|l, m\rangle=\hbar \sqrt{l(l+1)-m(m \pm 1)}|l, m \pm 1\rangle\)但是由于\(  |l, m\rangle\)本征函数是球谐函数的解，因此会有\( l \)是整数的要求。

电子的自旋和其他构成普通物质的粒子(质子、中子和电子)的自旋一样，都是\(  \displaystyle\frac { 1 }{ 2 } \)。用\(|s, m\rangle  \)来表示\( S^{2} \)和\( S_{z} \)的本征态的话，可以写成\(  \left|\displaystyle\frac{1}{2} \displaystyle\frac{1}{2}\right\rangle\)(spin up)和\( \left|\displaystyle\frac{1}{2}\left(-\displaystyle\frac{1}{2}\right)\right\rangle \)(spin down)两种状态。电子的自选状态可以表示为$$\chi=\left(\begin{array}{l} a \\ b \end{array}\right)=a \chi_{+}+b \chi_{-}=a\left(\begin{array}{l} 1 \\ 0 \end{array}\right)+b\left(\begin{array}{l} 0 \\ 1 \end{array}\right)$$两个列向量分别表示spin up和spin down。

由于两个自旋状态\(  \chi_{+} \)和\(    \chi_{-} \)都是其电子自旋的本征态，因此$$\mathbf{S}^{2} \chi_{+}=\frac{3}{4} \hbar^{2} \chi_{+}, \quad \mathbf{S}^{2} \chi_{-}=\frac{3}{4} \hbar^{2} \chi_{-}$$令\( \mathbf{S}^{2}=\left(\begin{array}{ll} c & d \\ e & f \end{array}\right) \)，\(\mathbf{S}  \)是一个自旋算符，对一个本征自旋态作用两次自旋算符，那么得到的特征值就是自旋角动量的平方，即\(\displaystyle\frac{3}{4} \hbar^{2}  \)。很容易解出$$\mathbf{S}^{2}=\frac{3}{4} \hbar^{2}\left(\begin{array}{ll} 1 & 0 \\ 0 & 1 \end{array}\right)$$类似的(两个本征态\(  \chi_{+}\)和\(  \chi_{-}\)对应的特征值为\(  \frac{\hbar}{2}\)和\(-\frac{\hbar}{2}  \))$$\mathbf{S}_{z} \chi_{+}=\frac{1}{2} \hbar \chi_{+}, \quad \mathbf{S}_{z} \chi_{-}=-\frac{1}{2} \hbar \chi_{-}$$求得\( \mathbf{S}_{z}=\frac{\hbar}{2}\left(\begin{array}{cc} 1 & 0 \\ 0 & -1 \end{array}\right) \)

另外\( \mathbf{S}_{+} \chi_{-}=\hbar \chi_{+}, \quad \mathbf{S}_{-} \chi_{+}=\hbar \chi_{-}, \quad \mathbf{S}_{+} \chi_{+}=\mathbf{S}_{-} \chi_{-}=0 \)，可以求得\( \mathbf{S}_{+}=\hbar\left(\begin{array}{ll} 0 & 1 \\ 0 & 0 \end{array}\right), \quad \mathbf{S}_{-}=\hbar\left(\begin{array}{ll} 0 & 0 \\ 1 & 0 \end{array}\right) \)，于是$$ \mathbf{S}_{x}=\frac{\hbar}{2}\left(\begin{array}{ll} 0 & 1 \\ 1 & 0 \end{array}\right), \quad \mathbf{S}_{y}=\frac{\hbar}{2}\left(\begin{array}{cc} 0 & -i \\ i & 0 \end{array}\right) $$改写上述结果有\( \mathbf{S}=(\hbar / 2) \sigma \)，其中$$\sigma_{x} \equiv\left(\begin{array}{cc} 0 & 1 \\ 1 & 0 \end{array}\right), \quad \sigma_{y} \equiv\left(\begin{array}{cc} 0 & -i \\ i & 0 \end{array}\right), \quad \sigma_{z} \equiv\left(\begin{array}{cc} 1 & 0 \\ 0 & -1 \end{array}\right)$$这就是“泡利自旋矩阵”。

\( \mathbf{S}_{x}, \mathbf{S}_{\mathbf{y}}, \mathbf{S}_{\mathbf{z}}, \mathbf{S}^2 \)都是厄米矩阵，\( \mathbf{S}_{+} ,\mathbf{S}_{-} \)不是厄米矩阵。

注：
1. 如果想知道某个算符的矩阵形式，那么可以用\( (\hat{Q})_{\operatorname{mn}}=\left\langle\operatorname{en}|\hat{Q}| e_{n}\right\rangle \)求解。
2. \( |a|^{2}+|b|^{2}=1\)，\(  |a|^{2}\)和\(  |b|^{2}\)分别表示量测到spin up和spin down的几率。
3. 上面的理解有问题，需要改正，另外课参考类比。

如果测量的是\( S_{x} \)，可能值是什么？几率又是多少？根据广义统计诠释，我们需要知道\(  \mathbf{S}_{x}\)的本征值和本征矢量。$$\frac{\hbar}{2}\left(\begin{array}{ll} 0 & 1 \\ 1 & 0 \end{array}\right)\left(\begin{array}{l} \alpha \\ \beta \end{array}\right)=\lambda\left(\begin{array}{l} \alpha \\ \beta \end{array}\right)$$将\(\lambda  \)移到左边，矩阵行列式为零，于是$$\left|\begin{array}{cc} -\lambda & \hbar / 2 \\ \hbar / 2 & -\lambda \end{array}\right|=0 \Rightarrow \lambda^{2}=\left(\frac{\hbar}{2}\right)^{2} \Rightarrow \lambda=\pm \frac{\hbar}{2}$$两个正负本征值对应的归一化的本征矢量为\( \chi_{+}^{(x)}=\left(\begin{array}{l} 1 / \sqrt{2} \\ 1 / \sqrt{2} \end{array}\right) \)和\( \chi_{-}^{(x)}=\left(\begin{array}{c} 1 / \sqrt{2} \\ -1 / \sqrt{2} \end{array}\right) \)。

接着我们用\(  \chi_{+}^{(x)}\)和\(  \chi_{-}^{(x)}\)作为正交基去张成\(  \chi\)的空间，为了求解基前面的系数，\( \chi=\left(\begin{array}{l} a \\ b \end{array}\right)=c_1 \chi_{+}^{(x)}+c_2 \chi_{-}^{(x)} \)，我们用基给等式两侧做内积，就会得到系数\(  c_1\)和\( c_2\)，于是有$$\chi=\left(\frac{a+b}{\sqrt{2}}\right) \chi_{+}^{(x)}+\left(\frac{a-b}{\sqrt{2}}\right) \chi_{-}^{(x)}$$如果测量\( S_{x} \)，得到\(  +\hbar / 2\)的几率是\((1 / 2)|a+b|^{2}  \)，得到\( -h / 2 \)的几率是\( (1 / 2)|a-b|^{2} \)。

磁场中的电子

一个带电的自旋粒子形成一个磁偶极子。它的磁偶矩\( \boldsymbol{\mu} \)正比于它的自旋角动量\(  \mathbf{S}\)$$\boldsymbol{\mu}=\gamma \mathbf{S}$$比例系数\(  \gamma\)称为回转磁比率。当一个磁偶极子放入一个磁场中，它受到的力矩为\( \boldsymbol{\mu} \times \mathbf{B} \)，使磁偶极子趋于磁场平行的方向(就像一个指南针一样)。这个力矩相应的能量为$$H=-\boldsymbol{\mu} \cdot \mathbf{B}$$所以一个静止在磁场中的带电的自旋粒子的哈密顿量是$$H=-\gamma \mathbf{B} \cdot \mathbf{S}$$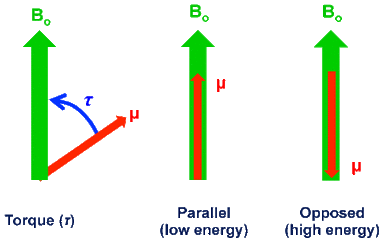

注：
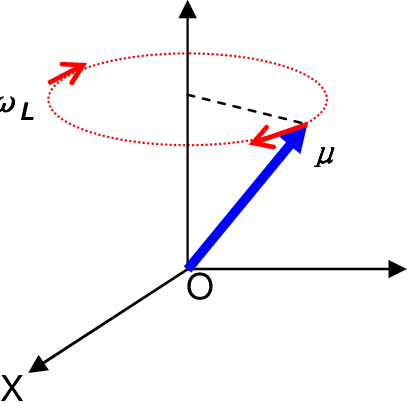
1. 力矩反映的是旋转效果，力矩越大说明转动的能力越大。力矩反映的是角动量在单位时间内的增量；力反应的是动量在单位时间内的增量。由于我们的力矩的方向始终和角动量的方向垂直，因此角动量的大小没有变化，只有方向上的变化，从上往下看，角动量的矢径就在做“画圆锥体”的运动。关于力矩和角动量可以看笔记物理学中的类比。
2. 上面的图片来自这里。我们也可以类比力矩公式\( \boldsymbol{\tau}=\mathbf{r} \times \mathbf{F} \)去理解。通过量纲判断，如果\(  \boldsymbol{\mu} \times \mathbf{B}\)的量纲对应力矩，那么\(  \boldsymbol{\mu} \cdot \mathbf{B}\)的量纲应该就是和\(\mathbf{r} \cdot\mathbf{F}  \)一致，显然就是能量。

拉莫尔进动

假定一个自旋\( \frac { 1 }{ 2 }  \)的粒子静止在一个方向沿着\(  z\)的均匀磁场中\(  \mathbf{B}=B_{0} \hat{k}\)，矩阵形式的哈密顿是$$\mathbf{H}=-\gamma B_{0} \mathbf{S}_{z}=-\frac{\gamma B_{0} \hbar}{2}\left(\begin{array}{cc} 1 & 0 \\ 0 & -1 \end{array}\right)$$ \( \mathbf{H} \)和\(  \mathbf{S}_{z}\)有相同的特征向量，但是特征值变为\( E_{+}=-\left(\gamma B_{0} \hbar\right) / 2 \)和\( E_{-}=+\left(\gamma B_{0} \hbar\right) / 2 \)。 显然当偶极矩平行磁场时能量最低⎯如同它的经典情况一样。由于哈密顿是不依赖时间的，含时薛定谔方程\(  i \hbar \displaystyle\frac{\partial \chi}{\partial t}=\mathbf{H} \chi\) 的一般解可以表示成定态的迭加： $$\chi(t)=a \chi_{+} e^{-i E_{+} t / \hbar}+b \chi_{-} e^{-i E_{-} t / \hbar}=\left(\begin{array}{c} a e^{i \gamma B_{0} t / 2} \\ b e^{-i \gamma B_{0} t / 2} \end{array}\right)$$我们令\( a=\cos (\alpha / 2), \quad b=\sin (\alpha / 2) \)，当然系数\( a \)和\(b  \)可以由初始条件\(  \chi(0)\)来确定，因此就可以确定一个固定不变的\( \alpha \)。于是有\(\chi(t)=\left(\begin{array}{c} \cos (\alpha / 2) e^{i \gamma B_{0} t / 2} \\ \sin (\alpha / 2) e^{-i \gamma B_{0} t / 2} \end{array}\right)  \) 为了对这样的态有一个感性认识，让我们计算\(  \mathbf{S}\) 期待值对时间的依赖关系： $$\begin{aligned} \left\langle S_{x}\right\rangle=& \chi(t)^{\dagger} \mathbf{S}_{x} \chi(t)=\left(\cos (\alpha / 2) e^{-i \gamma B_{0} t / 2} \quad \sin (\alpha / 2) e^{i \gamma B_{0} t / 2}\right) \\ & \times \frac{\hbar}{2}\left(\begin{array}{cc} 1 & 0 \\ 0 & -1 \end{array}\right)\left(\begin{array}{c} \cos (\alpha / 2) e^{i \gamma B_{0} t / 2} \\ \sin (\alpha / 2) e^{-i \gamma B_{0} t / 2} \end{array}\right) \\ &=\frac{\hbar}{2} \sin \alpha \cos \left(\gamma B_{0} t\right) \end{aligned}$$类似有$$\begin{array}{c} \left\langle S_{y}\right\rangle=\chi(t)^{\dagger} \mathbf{S}_{y} \chi(t)=\displaystyle\frac{\hbar}{2} \sin \alpha \sin \left(\gamma B_{0} t\right) \\ \left\langle S_{z}\right\rangle=\chi(t)^{\dagger} \mathbf{S}_{z} \chi(t)=\displaystyle\frac{\hbar}{2} \cos \alpha \end{array}$$显然\(  \langle\mathbf{S}\rangle\)和\( z \)轴有一个常数倾斜角\(\alpha   \) 并且绕磁场方向以 Larmor 频率\( \omega=\gamma B_{0} \) 进动，如同在经典情况中一样。

拉莫进动不是粒子真的在旋转，只是其自旋角动量的方向在不断变化，以电子为原点，以自旋角动量为矢量，那么画出来的就是一个圆锥体。自旋角动量的\( z \)轴分量在旋转过程中是保持不变的。其\( x \)轴和\(  y\)轴的投影分量都在做正余弦运动，而且两个分量的变化频率(正余弦的周期)是一致的，画在\(  x-y\)平面上的话其实就是下图中的虚线圆在\(  x-y\)平面的投影圆。可以参考这里。下图是表示\(\langle\mathbf{S}\rangle  \)在均匀磁场中的进动。

注：
1. 对于自旋产生的拉莫尔进动，角动量是自旋角动量，宏观上其实并不表现出自旋运动，只是电子的内在禀赋，这一点要和轨道角动量区分开来。
2. 电子绕原子核也有拉莫尔进动，这个时候考虑的就是轨道角动量反方向的磁矩，以及磁矩和磁场相互作用产生的力矩造成的圆周运动。
3. 物理学中的拉莫尔进动是指电子、原子核和原子的磁矩在外部磁场作用下的进动。总而言之对电子来说，既有基于轨道角动量(轨道磁矩)的拉莫尔进动，也有基于自旋角动量(自旋磁矩)的拉莫尔进动，可以参考这里。

施特恩-格拉赫实验

待补充

角动量的叠加

假设现在我们有两个自旋\(  \)的例子，比如处于氢原子基态的电子和质子，那么有自旋组合有四种可能性：(前者对应电子，后者对应质子)$$\uparrow \uparrow, \uparrow \downarrow, \downarrow \uparrow, \downarrow \downarrow$$现在问题来了，这个原子的总角动量是什么？令\(  \mathbf{S} \equiv \mathbf{S}^{(1)}+\mathbf{S}^{(2)}\)，这四个复合态都是\( S_{z} \)的一个本征态-\(  z\)分量的简单加在一起：$$\begin{aligned} S_{z} \chi_{1} \chi_{2} &=\left(S_{z}^{(1)}+S_{z}^{(2)}\right) \chi_{1} \chi_{2}=\left(S_{z}^{(1)} \chi_{1}\right) \chi_{2}+\chi_{1}\left(S_{z}^{(2)} \chi_{2}\right) \\ &=\left(\hbar m_{1} \chi_{1}\right) \chi_{2}+\chi_{1}\left(\hbar m_{2} \chi_{2}\right)=\hbar\left(m_{1}+m_{2}\right) \chi_{1} \chi_{2} \end{aligned}$$注意\( S_{z}^{(1)} \)只作用在\(\chi_{1}  \)上，\( S_{z}^{(2)} \)只作用在\(  \chi_{2}\)上。所以\(  m\)(复合系统的量子数)就是\( m_1+m_2 \): $$\begin{aligned} &\uparrow \uparrow: m=1\\ &\uparrow \downarrow: m=0\\ &\downarrow \uparrow: m=0\\ &\downarrow \downarrow: m=-1 \end{aligned}$$于是复合系统的自旋为\(  s=1\)，\(  m\)应该是从\(  -s\)往\(  +s\)变化，多出来的一个\(  m=0\)，我们可以把两种\(  m=0\)的状态看成\( m=0 \)的叠加态的基元。我们可以利用降阶算符作用在\( m=1 \)的态上看一下效果$$\begin{aligned} S_{-}(\uparrow \uparrow) &=\left(S_{-}^{(1)} \uparrow\right) \uparrow+\uparrow\left(S_{-}^{(2)} \uparrow\right) \\ &=(\hbar \downarrow) \uparrow+\uparrow(\hbar \downarrow)=\hbar(\downarrow \uparrow+\uparrow \downarrow) \end{aligned}$$显然\( s=1 \)的三个态用\(  |s \, m\rangle\)来表示为：$$\left\{\begin{array}{l} |11\rangle=\uparrow \uparrow \\ |10\rangle=\displaystyle\frac{1}{\sqrt{2}}(\uparrow \downarrow+\downarrow \uparrow) \\ |1-1\rangle=\downarrow \downarrow \end{array}\right\} \quad s=1 \text { (triplet) }$$对于标准的自旋\(  s=1\)的系统，有我们这里的双电子自旋的系统三重态似乎和这里的\(s=1  \)的系统很类似，可以验证一下我们的三重态，用\(  \mathbf{S}\)作用两次，看得到的特征值是不是\(  s(s+1) \hbar^{2}=1(1+1) \hbar^{2}\)。我们先写出$$S^{2}=\left(\mathbf{S}^{(1)}+\mathbf{S}^{(2)}\right) \cdot\left(\mathbf{S}^{(1)}+\mathbf{S}^{(2)}\right)=\left(\mathbf{S}^{(1)}\right)^{2}+\left(\mathbf{S}^{(2)}\right)^{2}+2 \mathbf{S}^{(1)} \cdot \mathbf{S}^{(2)}$$根据\(  S_{x/y/z}\)的特性，我们又有$$\begin{aligned} \mathbf{S}^{(1)} \cdot \mathbf{S}^{(2)}(\uparrow \downarrow) &=\left(S_{x}^{(1)} \uparrow\right)\left(S_{x}^{(2)} \downarrow\right)+\left(S_{y}^{(1)} \uparrow\right)\left(S_{y}^{(2)} \downarrow\right)+\left(S_{z}^{(1)} \uparrow\right)\left(S_{z}^{(2)} \downarrow\right) \\ &=\left(\frac{\hbar}{2} \downarrow\right)\left(\frac{\hbar}{2} \uparrow\right)+\left(\frac{i \hbar}{2} \downarrow\right)\left(\frac{-i \hbar}{2} \uparrow\right)+\left(\frac{\hbar}{2} \uparrow\right)\left(\frac{-\hbar}{2} \downarrow\right) \\ &=\frac{\hbar^{2}}{4}(2 \downarrow \uparrow-\uparrow \downarrow) \end{aligned}$$用\( \downarrow \uparrow \)去替换\(  \uparrow \downarrow\)，于是得到\(\displaystyle\frac{\hbar^{2}}{4}(2 \uparrow \downarrow-\downarrow \uparrow) \)。那么\( \mathbf{S}^{(1)} \cdot \mathbf{S}^{(2)} \)作用在\(  |10\rangle\)即\( \displaystyle\frac{1}{\sqrt{2}}(\uparrow \downarrow+\downarrow \uparrow) \)上，有$$\mathbf{S}^{(1)} \cdot \mathbf{S}^{(2)}|10\rangle=\frac{\hbar^{2}}{4} \frac{1}{\sqrt{2}}(2 \downarrow \uparrow-\uparrow \downarrow+2 \uparrow \downarrow-\downarrow \uparrow)=\frac{\hbar^{2}}{4}|10\rangle$$

根据前面的\(  \mathbf{S}^{2} \chi_{+}=\displaystyle\frac{3}{4} \hbar^{2} \chi_{+}, \quad \mathbf{S}^{2} \chi_{-}=\displaystyle\frac{3}{4} \hbar^{2} \chi_{-}\)，当\( \left(\mathbf{S}^{(1)}\right)^{2} \)作用在\(  \uparrow \downarrow\)上时，实际上只是作用在\(  \uparrow\)上，后面的\(  \downarrow\)的状态保持不变，因此有\(  \left(\mathbf{S}^{(1)}\right)^{2}(\uparrow \downarrow)=\left(\left(\mathbf{S}^{(1)}\right)^{2} \uparrow\right) \downarrow=\displaystyle\frac{3}{4} \hbar^{2} \uparrow \downarrow  \quad \left(\mathbf{S}^{(1)}\right)^{2}(\downarrow \uparrow)=\left(\left(\mathbf{S}^{(1)}\right)^{2} \downarrow\right) \uparrow=\displaystyle\frac{3}{4} \hbar^{2} \downarrow \uparrow\)即有$$(\mathbf{S}^{(1)})^2 |10\rangle=\frac {3 }{ 4 } \hbar^2|10\rangle$$同样地，\(  (\mathbf{S}^{(2)})^2 |10\rangle=\displaystyle\frac {3 }{ 4 } \hbar^2|10\rangle\)，因此最终有$$\mathbf{S}^{2}|10\rangle=\left(\frac{3 \hbar^{2}}{4}+\frac{3 \hbar^{2}}{4}+2 \frac{\hbar^{2}}{4}\right)|10\rangle=2 \hbar^{2}|10\rangle$$所以\( |10\rangle \)确实是\( S^{2}\)本征值为\( 2 \hbar^{2} \)的本征态。同样地，也有$$\mathbf{S}^{2}|00\rangle=\left(\frac{3 \hbar^{2}}{4}+\frac{3 \hbar^{2}}{4}-2 \frac{3 \hbar^{2}}{4}\right)|00\rangle=0$$即有\( |00\rangle \)是\(S^{2}  \)本征值为\(  0\)的本征态。

下面我们谈谈什么是\(  |00\rangle\)。两个电子自旋排列组合有四种独立情况(state)，那么显然要囊括所有这四种情况，必须要有四个基底，而前面我们讨论的系统自旋为\(  s=1\)的情况只是三重态，也就是说少了一个基底。其实我们会发现这个三重态的三个基底(状态)的线性组合不能得到\( \uparrow \downarrow \)或者\( \downarrow \uparrow \)。实际上，当然也必须是，还存在一个自旋\(  s=0\)的态，那么\(  m\)在正负\( s \)内变化，显然只能取\(  m=0\)，那么这就是一个“单态”，即$$\left\{|00\rangle=\frac{1}{\sqrt{2}}(\uparrow \downarrow-\downarrow \uparrow)\right\} \quad s=0 \text { (singlet) }$$

注：
1. \(\mathbf{S}^{(1)}  \)和\(\mathbf{S}^{(2)}  \)相互看不见(无关联)，所以它们是互易的，相乘的时候谁放在前面都无所谓。
2. 电子的自旋是\(  \displaystyle\frac {  1}{2  } \)，其分布遵守的是费米狄拉克统计分布，而对于自旋为\( 1 \)的粒子，其遵守的是波色爱因斯坦分布。所以两个自旋为\(  \displaystyle\frac {  1}{2  } \)的电子系统变成了自旋为\(  1\)的“粒子”，这意味着其分布也将发生变化。
3. 对于\(  \uparrow \uparrow\)或者\( \downarrow \downarrow \)来说，两个电子交换不改变state，但是对于\( \uparrow \downarrow \)或者\(  \downarrow \uparrow\)来说交换会改变state。对于前面讨论的三重态，两个电子交换结果还是一样，即对exchange来说是symmetry，而对于单态来说，交换两个电子结果会出现一个负号，即对excahnge来说是anti-symmetry。
4. 如果将自旋为\(  s_{1}\)和自旋为\(  s_{2}\)的两个粒子结合，得到的系统的总自旋为\(  s=\left(s_{1}+s_{2}\right),\left(s_{1}+s_{2}-1\right),\left(s_{1}+s_{2}-2\right), \ldots,\left|s_{1}-s_{2}\right|\)，最大值和最小值分别出现在自旋平行和自旋相反的情况。

量子力学中的洛伦兹力