量子力学

测不准原理

普遍不确定原理的证明

对任意可观测量\(A  \) (i.e. \(\hat{A}\)，下式中\( f \equiv(\hat{A}-\langle A\rangle) \Psi \))$$\sigma_{A}^{2}=\langle(\hat{A}-\langle A\rangle)^{2}\rangle=\langle \Psi |(\hat{A}-\langle A\rangle)^2 \Psi\rangle=\langle(\hat{A}-\langle A\rangle) \Psi |(\hat{A}-\langle A\rangle) \Psi\rangle=\langle f | f\rangle$$同理对任意可观测量\(B\)有\(\sigma_{B}^{2}=\langle g | g\rangle\)，其中\( g \equiv(\hat{B}-\langle B\rangle) \Psi \)。

  • \(\sigma_{A}^{2} \sigma_{B}^{2}=\langle f \mid f\rangle\langle g \mid g\rangle\)
  • Schwarz不等式 \(\langle f \mid f\rangle\langle g \mid g\rangle \geq|\langle f \mid g\rangle|^{2}\)
  • 对任意复数\(z\)有\(|z|^{2}=[\operatorname{Re}(z)]^{2}+[\operatorname{Im}(z)]^{2} \geq[\operatorname{Im}(z)]^{2}=\left[\displaystyle\frac{1}{2 i}\left(z-z^{*}\right)\right]^{2}\)
  • 令\(  z=\langle f | g\rangle\)，有$$\sigma_{A}^{2} \sigma_{B}^{2}\geq|\langle f \mid g\rangle|^{2}\geq\left(\frac{1}{2 i}[\langle f \mid g\rangle-\langle g \mid f\rangle]\right)^{2}$$

下面计算\(\langle f \mid g\rangle\)的结果(注意下面的\(\langle A\rangle\)和\(\langle B\rangle \)表示的是纯数值，所以随便交换顺序都不影响)$$\begin{aligned} \langle f | g\rangle &=\langle(\hat{A}-\langle A\rangle) \Psi |(\hat{B}-\langle B\rangle) \Psi\rangle=\langle\Psi |(\hat{A}-\langle A\rangle)(\hat{B}-\langle B\rangle) \Psi\rangle \\ &=\langle\Psi |(\hat{A} \hat{B}-\hat{A}\langle B\rangle-\hat{B}\langle A\rangle+\langle A\rangle\langle B\rangle) \Psi\rangle \\ &=\langle\Psi | \hat{A} \hat{B} \Psi\rangle-\langle B\rangle\langle\Psi | \hat{A} \Psi\rangle-\langle A\rangle\langle\Psi | \hat{B} \Psi\rangle+\langle A\rangle\langle B\rangle\langle\Psi | \Psi\rangle \\ &=\langle\hat{A} \hat{B}\rangle-\langle B\rangle\langle A\rangle-\langle A\rangle\langle B\rangle+\langle A\rangle\langle B\rangle \\ &=\langle\hat{A} \hat{B}\rangle-\langle A\rangle\langle B\rangle \end{aligned}$$同理\( \langle g | f\rangle=\langle\hat{B} \hat{A}\rangle-\langle A\rangle\langle B\rangle \)，于是$$\langle f | g\rangle-\langle g | f\rangle=\langle\hat{A} \hat{B}\rangle-\langle\hat{B} \hat{A}\rangle=\langle\hat{A} \hat{B}-\hat{B} \hat{A}\rangle=\langle[\hat{A}, \hat{B}]\rangle$$式中两个算符是对易关系\(  [\hat{A}, \hat{B}] \equiv \hat{A} \hat{B}-\hat{B} \hat{A}\)，于是$$\sigma_{A}^{2} \sigma_{B}^{2} \geq\left(\frac{1}{2 i}\langle[\hat{A}, \hat{B}]\rangle\right)^{2}$$这就是更普遍的测不准原理。位置和动量算符的对易关系\( [\hat{x}, \hat{p}]=i \hbar \)，于是\(\sigma_{x}^{2} \sigma_{p}^{2} \geq\left(\displaystyle\frac{\hbar}{2}\right)^{2}\)

  • 如果\( [\hat{A}, \hat{B}]=0\)(可对易)，那么测就不存在测不准原理，\(A  \)和\(  B\)可以同时测得无限准，如\(\left[x, x^{2}\right]=0  \)；
  • commutator不等于零的时候，就会有测不准原理；
  • 测不准原理本来说是，你观测\(A\)，那么波函数就会坍塌到一个本征态(本征函数)，量到的结果就是本征值，那么这次测量会对下次测量有影响(如果二者不对易)；
  • \(\hat{A}\) 和 \(\hat{B}\) 具有对易关系和它们具有相同的本征函数是等价的(想一下这个时候的测不准原理)：
    • 如果 \(\hat{A} \hat{B}-\hat{B} \hat{A}=0\) (即 \(\hat{A}\) 和 \(\hat{B}\) 具有对易关系)，那么对任意函数\(f\)有\(\hat{A} \hat{B}|f\rangle=\hat{B}\hat{A}|f\rangle\)
    • 有相同本征函数\( \left\{\begin{array}{l} \hat{A}\left|f_{n}\right\rangle=a_{n}\left|f_{n}\right\rangle \\ \hat{B}\left|f_{n}\right\rangle=b_{n}\left|f_{n}\right\rangle \end{array}\right. \)可推出\(\hat{A} \hat{B}\left|f_{n}\right\rangle=\hat{A} b_{n}\left|f_{n}\right\rangle=a_{n} b_{n}\left|f_{n}\right\rangle=\hat{B} \hat{A}\left|f_{n}\right\rangle\)

参考资料：
(1) 对于量子力学的不确定性原理，为什么会存在「算符不对易」与「傅里叶变换」两种解释?—知乎
(2) 不确定性原理的前世今生—博客园

能量-时间不确定原理

我们知道坐标-动量不确定原理 \(\Delta x \Delta p \geq \displaystyle\frac{\hbar}{2}\)，而能量-时间不确定原理\(\Delta t \Delta E \geq \displaystyle\frac{\hbar}{2}\)实际上是一个完全不同的概念，虽然二者形式上看起来差不多。坐标、动量和能量都是动力学变量 — 是体系在任何时刻都可观测的特征。但是时间本身不是动力学变量：你不会像测量坐标和 能量一样去测量一个粒子的“时间”。时间是一个独立变量，动力学量是它的函数。

当测量一个体系变化有多快时，我们来求某个可观测量\(Q(x, p, t)\)的期望值对时间的导数$$ \frac{d}{d t}\langle Q\rangle=\frac{d}{d t}\langle\Psi \mid \hat{Q} \Psi\rangle=\left\langle\frac{\partial \Psi}{\partial t} \mid \hat{Q} \Psi\right\rangle+\left\langle\Psi \mid \frac{\partial \hat{Q}}{\partial t} \Psi\right\rangle+\left\langle\Psi \mid \hat{Q} \frac{\partial \Psi}{\partial t}\right\rangle $$由薛定谔方程\(i \hbar \displaystyle\frac{\partial \Psi}{\partial t}=\hat{H} \Psi\)所以$$ \frac{d}{d t}\langle Q\rangle=-\frac{1}{i \hbar}\langle\hat{H} \Psi \mid \hat{Q} \Psi\rangle+\frac{1}{i \hbar}\langle\Psi \mid \hat{Q} \hat{H} \Psi\rangle+\left\langle\frac{\partial \hat{Q}}{\partial t}\right\rangle $$\(\hat{H}\)是厄米算符，于是有\(\langle\hat{H} \Psi \mid \hat{Q} \Psi\rangle=\langle\Psi \mid \hat{H} \hat{Q} \Psi\rangle\)，因此$$ \frac{d}{d t}\langle Q\rangle=\frac{i}{\hbar}\langle[\hat{H}, \hat{Q}]\rangle+\left\langle\frac{\partial \hat{Q}}{\partial t}\right\rangle $$根据广义不确定原理，并且如果我们这里\(\frac{\partial \hat{Q}}{\partial t}=0\)，那么$$ \sigma_{H}^{2} \sigma_{Q}^{2} \geq\left(\frac{1}{2 i}\langle[\hat{H}, \hat{Q}]\rangle\right)^{2}=\left(\frac{1}{2 i} \frac{\hbar}{i} \frac{d\langle Q\rangle}{d t}\right)^{2}=\left(\frac{\hbar}{2}\right)^{2}\left(\frac{d\langle Q\rangle}{d t}\right)^{2} $$或者，更简洁地$$ \sigma_{H} \sigma_{Q} \geq \frac{\hbar}{2}\left|\frac{d\langle Q\rangle}{d t}\right| $$我们定义\(\Delta E \equiv \sigma_{H}\)以及\(\Delta t \equiv \displaystyle\frac{\sigma_{Q}}{|d\langle Q\rangle / d t|}\)，则有$$ \Delta E \Delta t \geq \frac{\hbar}{2} $$

  • \(\Delta t\)是 the amount of time it takes the system to change by one sort of standard deviation of the observable in question.
  • \(\Delta t\)表示\(Q\) 的期望值变化单位标准差时所需的时间。
  • 这里的\(\Delta t\)不是一次测量时间尺度上耗时的uncertainty；
  • \(\Delta t\) for the system是没有意义的，有意义的是\(\Delta t\) for mementum/position/kinetic energy，即\(\Delta t\)完全依赖于你所关心的那个可观测量\(Q\)。
  • 如果系统快速变化，使得我们感兴趣的可观测量\(Q\)也变化很快，即\(\displaystyle\frac{d}{d t}\langle Q\rangle\)很大，这意味着\(\Delta t\) would be small，这意味着uncertainty in the energy will be large。
  • 如果系统快速变化，it has to consist of a superposition of a wide range of different energies。
  • 这里的\(Q\)是任意可观测量，也就是说任意可观测量快速变化，那么能量的不确定性就会很小。换句话说，只要能量的不确定性很小(即we're dealing with sort of a determinate state with almost )，那么任意可观测量变化速率就会很小(\(\displaystyle\frac{d}{d t}\langle Q\rangle\)很小)，极限情况就是我们之前说的stationary state (eigenstate of Hamiltonian operator)，能量的不确定的为零，\(\Delta t\)为无限大。

 

 

狄拉克符号

三种方式表示波函数

从线性代数我们知道，要描述空间中的一个向量，可以按照不同的方式选取线性无关的基向量组。当然为了方便我们通常选取相互正交而且模长为\(1  \)的作为基向量组，即使这样，通过旋转，我们还是可以得到新的基向量组。形象比喻就是，为了表示一个中文叫作“狗”的东西，英文、法文、德文等都有自己对应的单词，我们虽然用的是不同的语言，但是描述的是同一个东西；我们虽然用的是不同的基向量组，但是都可以通过它们的线性组合来得到已知向量。

先前我们描述波函数空间，思路是先求解出某一时刻的波函数在各点\(  x\)的状态，然后加上时间的相位因子，即可以描述波函数随着时间的演变，其实这就是我们说的【坐标空间波函数】。通过傅里叶变换，可以很容易将坐标空间波函数变成【动量空间波函数】，二者包含同等容量的信息。坐标空间当然比较容易想象，动量空间就比较抽象了；无论是用哪个空间来描述，波函数都是其中的本征函数的线性组合，当然本征值分立的情况比较容易理解，对于连续谱来说，单一本征函数不可归一化，但是无数本征函数(对应本征值连续)线性组合的波函数是可以归一化的。对于波函数来说，本征函数集，除了从坐标和动量的角度选取，还有很多其他的选取方式，下面开始详细介绍。

为了简单起见，这里我们不考虑时间的相位因子，即只讨论time-independent的情况，对于任意不含时的波函数(矢量)\(|\psi\rangle\)，坐标、动量、能量等是动力学变量，我们只需要用任一动力学变量就可以描述这个波函数，或者说描述波函数的状态。选取不同的动力学变量，就是选取不同的基底(也是就是基矢量/本征函数)，这里的基底也是动力学变量算符的本征函数，于是波函数可以描述为一组系数，这组系数对基矢量的线性组合的加和函数。

  • 坐标空间，\(\hat{x}|x\rangle=x|x\rangle\)，本征值\(x\)，本征函数为\(|x\rangle=f_x(p)=\displaystyle\frac{e^{-\frac{i p x}{\hbar}}}{\sqrt{2 \pi \hbar}}\)，算符\(\hat{x}=-\displaystyle\frac{\hbar}{i} \frac{d}{d p}\)$$ \psi(x)=\langle x \mid \psi\rangle $$注：\(\psi(x)=\displaystyle\int_{-\infty}^{\infty} \phi(p) \frac{e^{ \frac{ip x}{\hbar}}}{\sqrt{2 \pi \hbar}} d p=\int_{-\infty}^{\infty} \delta(x-\xi) \psi(\xi) d \xi\)
  • 动量空间，\(\hat{p}|p\rangle=p|p\rangle\)，本征值\(p\)，本征函数为\(|p\rangle=f_p(x)=\displaystyle\frac{e^{\frac{i p x}{\hbar}}}{\sqrt{2 \pi \hbar}}\)，算符\(\hat{p}=\displaystyle\frac{\hbar}{i} \frac{d}{d x}\)$$ \phi(p)=\langle p \mid \psi\rangle $$注：\(\phi(p)=\displaystyle\int_{-\infty}^{\infty} \frac{e^{-\frac{ip x}{\hbar}}}{\sqrt{2 \pi \hbar}} \psi(x) d x\)
  • 能量空间，假设是分离谱，\(\hat{H}|\psi_n\rangle=E_{n}|\psi_n\rangle\)，本征值\(E_{n}\)，本征函数为\(|\psi_n\rangle\)。$$c_{n}=\left\langle\psi_{n} \mid \psi\right\rangle $$
  • 总结：\(|\psi\rangle\)状态可以用\(\psi(x)\)、\(\phi(p)\)以及\(\left\{c_{n}\right\}\)等等来独立来表示。

(1) $$\Psi(x, t)=c_x (t)=\langle x | \mathfrak{I}(t)\rangle$$我们这样理解这个式子：我们先假定\( x \)是一个定值，那么该点的波动随时间的演化，其实就是从\( \Psi(x, t) \)中摘出\(  x\)这个点的信息(其实等式中\(\langle x  \)写成\(\langle \hat{x}  \)可能更好理解)  。\( |\mathfrak{J}(t)\rangle \)是希尔伯特空间中波函数的矢量，形象说就是“狗”这种动物。\(  \langle x| \mathfrak{I}(t)\rangle\)中的\(  x\)其实就是\(\mathfrak{J}(t)  \)的某一个eigenstate(position的eigenfunction)，二者内积得到对应eigenstate的某个系数，这些系数共同组成了函数本身。\(  \Psi(x, t)\)就是\(x\) position eigenfunction的系数。可以对比之前的\(\left\langle f_{m} | f\right\rangle=c_m\)

这里的基矢量\(|x\rangle  \)是属于本征值\(  x\)的\(\hat{x}  \)本征函数，即\(  \hat{x}|x\rangle=x|x\rangle\)，这里的\(|x\rangle  \)其实是\(\delta(x-y)  \)(对比我们前面的\(x g_{y}(x)=y g_{y}(x)  \))，但是我们现在不会混淆了；其实意思就是通过坐标算符的作用，从一堆\(x  \)中随机挑出一个。那么算符\( \hat{x} \)与\(  \Psi(x, t)\)作用就是挑出其中某个\(x  \)位置的信息\( \hat{x} \Psi(x, t)=\delta(x-y) \Psi(x, t) \)，变化\(\delta(x-y)  \)中\( y \)的值，我们就可以得到无数个“本征函数”，其实这里的本征函数，我们也可以认为是线性组合系数，对应于本征函数\(|x\rangle  \)，就可以组合成\(  |\mathfrak{J}(t)\rangle\)。

(2) $$\Phi(p, t)=\langle p | \Im(t)\rangle$$这里的基矢量\(|p\rangle  \)是属于本征值\(  p\)的\(\hat{p}  \)本征函数，其实是坐标空间的\(  f_{p}(x)\)。\( \Phi(p, t) \)就是动量\(p\) eigenfunction的系数。

(3)  假设谱是分立的，用能量本征函数的基展开  $$c_{n}(t)=\langle n | \mathfrak{I}(t)\rangle$$这里的基矢量\(|n\rangle  \)是属于\(  \hat{H}\)的第\( n \)个本征函数，注意不是“\(  n\)”。\( c_n(t) \)就是厄米算符的eigenfunction的系数。\(\hat{H}|n\rangle=E_{n}|n\rangle  \)

函数\( \Psi \)、\( \Phi \)和系数的集合\( \left\{c_{n}\right\} \)精确包含同样的信息-它们仅是描述同一矢量的三种不同途径而已。需求不同，选定方式不同。

算符的矩阵表示

厄米算符是一种线性变换，下面推导矩阵\(  \hat{Q}\)的形式$$|\beta\rangle=\hat{Q}|\alpha\rangle$$现在我们以“标准正交”的\( \left\{\left|e_{n}\right\rangle\right\} \)作为基底，那么$$\begin{aligned} &|\alpha\rangle=\sum_{n} a_{n}\left|e_{n}\right\rangle, \quad a_{n}=\left\langle e_{n} \mid \alpha\right\rangle\\ &|\beta\rangle=\sum_{n} b_{n}\left|e_{n}\right\rangle, \quad b_{n}=\left\langle e_{n} \mid \beta\right\rangle \end{aligned} $$于是算符线性变换的方程可以表示为$$\sum_{n} b_{n}\left|e_{n}\right\rangle=\hat{Q}\sum_{n} a_{n}\left|e_{n}\right\rangle=\sum_{n} a_{n} \hat{Q}\left|e_{n}\right\rangle$$两边同时取\(  \left|e_{m}\right\rangle\)的内积$$\sum_{n} b_{n}\left\langle e_{m} | e_{n}\right\rangle=\sum_{n} a_{n}\langle e_{m}|\widehat{Q}| e_{n}\rangle$$等式左侧\( \left\langle e_{m} | e_{n}\right\rangle\)其实就是\(\delta_{mn}\)，于是左侧等于\(b_m\)；等式右侧，令\( \langle e_{m}|\hat{Q}| e_{n}\rangle=Q_{m n}\)，将右侧进行改写，因此最后等式改写为$$b_{m}=\sum_{n} Q_{m n} a_{n}$$矩阵\(Q_{m n}\)就是observable operator \(\hat{Q}\)的矩阵。\(\hat{Q} | e_{n}  \)就是挑出矩阵的第\(n  \)列，而\( \left\langle e_{m}|\hat{Q}| e_{n}\right\rangle \)就是挑出第\( n \)列的，第\( m \)行的单一元素\(Q_{m n}  \)。我们暂时讨论的是离散的，后面再说连续的情况。不同的基底会有不同的observable operator/linear transformation MATRIX

投影算符(projection Operator)

线性代数中的投影矩阵参考线性代数-1笔记。

我们已经知道\(\langle\alpha | \alpha\rangle  \)是内积，结果是一个数，那么\(|\alpha\rangle\langle\alpha|\)是什么的呢？我们可以让它作用在一个向量(右矢，也是函数)，看看结果是什么，类似放一个测试函数\(|\beta\rangle\)，然后就可以看出它真正的作用是什么了。事实上\( \hat{P} \equiv|\alpha\rangle\langle\alpha|\)为【投影矩阵】(也是projection operator)，作用于\(|\beta\rangle\)，得到的是沿着\(|\alpha\rangle\)向量方向的一个新的向量，也就是说\(|\beta\rangle\)在\(|\alpha\rangle\)方向的投影向量为\(\langle\alpha | \beta\rangle|\alpha\rangle\)。$$\hat{P}|\beta\rangle=|\alpha\rangle\langle\alpha | \beta\rangle=\langle\alpha | \beta\rangle|\alpha\rangle$$

如果\( \left\{\left|e_{n}\right\rangle\right\} \)是分立的标准正交基组合(基底，描述一个空间)，那么\(\left|e_{n}\right\rangle\left\langle e_{n}\right|\)也会是projection operator，同样地，我们将其作用在测试向量\(|\alpha\rangle\)上，注意\(|\alpha\rangle=\displaystyle\sum_{n}a_n|e_{n}\rangle\)，于是可以得到(\(n\)是特定的，\(m\)是变化的，以示区分)$$|e_{n}\rangle\langle e_{n} | \alpha\rangle =|e_{n}\rangle\langle e_{n} | \displaystyle\sum_{m}a_m|e_{m}\rangle=a_n|e_n\rangle$$如果将所有的投影矩阵(\( |e_{n}\rangle\langle e_{n} |\)不同的\( n\)值)都作用在测试函数上(任意选取)，然后加和有$$\sum_{n}\left|e_{n}\right\rangle\left\langle e_{n} | \alpha\right\rangle= \sum_{n} a_{n}\left|e_{n}\right\rangle=|\alpha\rangle$$因此\( \displaystyle\sum_{n}\left|e_{n}\right\rangle\left\langle e_{n}\right|=1 \)(注：严格来说应该等于单位阵)，这说明这是一个完整的基底，即所有基底对应的projection operator做summation等于\( 1\)。

类似的，假如\( \left\{\left|e_{z}\right\rangle\right\} \)是狄拉克正交归一的连续基(连续谱)，那么$$\left\langle e_{z} | e_{z^{\prime}}\right\rangle=\delta\left(z-z^{\prime}\right)$$则有\(  \displaystyle\int\left|e_{z}\right\rangle\left\langle e_{z}\right| d z=1\)。所以$$ \begin{aligned} &\Rightarrow \int\left|e_{z}\right\rangle\left\langle e_{z} \mid \alpha\right\rangle d z \\ &=\int c_{z}\left|e_{z}\right\rangle d z \\ &=|\alpha\rangle \end{aligned} $$

Two level system振荡(解耦)

例子：two level system，\( |1\rangle=\left(\begin{array}{l} 1 \\ 0 \end{array}\right) \)，\( |2\rangle=\left(\begin{array}{l} 0 \\ 1 \end{array}\right) \)

这个系统的哈密顿算符为\( H=\left(\begin{array}{ll} h & g \\ g & h \end{array}\right) \)，其中\( g \)和\( h\)都为实数，为什么这么写暂时先不管。

要想知道系统随着时间的演化，只需要知道哈密顿算符、基底以及初始条件。上面的哈密顿算符也属于厄米矩阵，只有厄米矩阵才能满足厄米算符的特性\( \langle f | \hat{Q}g\rangle=\langle\hat{Q} f | g\rangle \)。我们说的厄米矩阵，比如\(\left[\begin{array}{cc} 2 & 3+i \\ 3-i & 5 \end{array}\right]  \)，转置之后取共轭和自身相等，这样的矩阵叫厄米矩阵。由于我们这里的哈密顿算符矩阵都是实数，所以看起来就是对称的，如果非对角线含有虚数部分，那么就不对称了。

含时薛定谔方程为$$i \hbar \frac{d}{d t}|\mathfrak{I}(t)\rangle=H|\mathfrak{I}(t)\rangle$$我们先通过分离变数法，去掉时间项\( e^{-i E t / \hbar} \)。于是可以根据\(\left(\begin{array}{ll}h & g \\ g & h\end{array}\right)\left(\begin{array}{l}a \\ b\end{array}\right)=E\left(\begin{array}{l}a \\ b\end{array}\right)\)确定本征值(其中的\(  a\)和\( b\)是不同状态的系数，\(a^2+b^2=1\))$$\operatorname{det}\left(\begin{array}{cc} h-E & g \\ g & h-E \end{array}\right)=(h-E)^{2}-g^{2}=0 \Rightarrow h-E=\mp g \Rightarrow E_{\pm}=h \pm g$$接着很容易求出对应的特征向量，进行归一化(归一化其实是让两个状态的出现的概率之和为\(  1\))得到两个不同特征值下的特征向量为$$\left|\mathfrak{I}_{\pm}\right\rangle=\frac{1}{\sqrt{2}}\left(\begin{array}{c} 1 \\ \pm 1 \end{array}\right)$$初始状态为两个本征向量(状态)的线性叠加(确定组合系数，类似以前的\( c_n \))$$|\Im(0)\rangle=\left(\begin{array}{l} 1 \\ 0 \end{array}\right)=\frac{1}{\sqrt{2}}\left(\left|\mathfrak{I}_{+}\right\rangle+\left|\mathfrak{I}_{-}\right\rangle\right)$$加入时间因子$$\begin{aligned} |\mathfrak{J}(t)\rangle &=\frac{1}{\sqrt{2}}\left[e^{-i(h+g) t / \hbar}\left|\mathfrak{J}_{+}\right\rangle+e^{-i(h-g) t / \hbar}\left|\mathfrak{J}_{-}\right\rangle\right] \\ &=\frac{1}{2} e^{-i h t / \hbar}\left[e^{-i g t / \hbar}\left(\begin{array}{c} 1 \\ 1 \end{array}\right)+e^{i g t / \hbar}\left(\begin{array}{c} 1 \\ -1 \end{array}\right)\right] \\ &=\frac{1}{2} e^{-i h t / \hbar}\left(\begin{array}{c} e^{-i g t / \hbar}+e^{i g t / \hbar} \\ e^{-i g t / \hbar}-e^{i g t / \hbar} \end{array}\right)=e^{-i h t / \hbar}\left(\begin{array}{c} \cos (g t / \hbar) \\ -i \sin (g t / \hbar) \end{array}\right) \end{aligned}$$这里的\( e^{-i h t / \hbar} \)是一个相位项phase term，算波函数概率的时候，内积相互抵消了，不影响概率密度。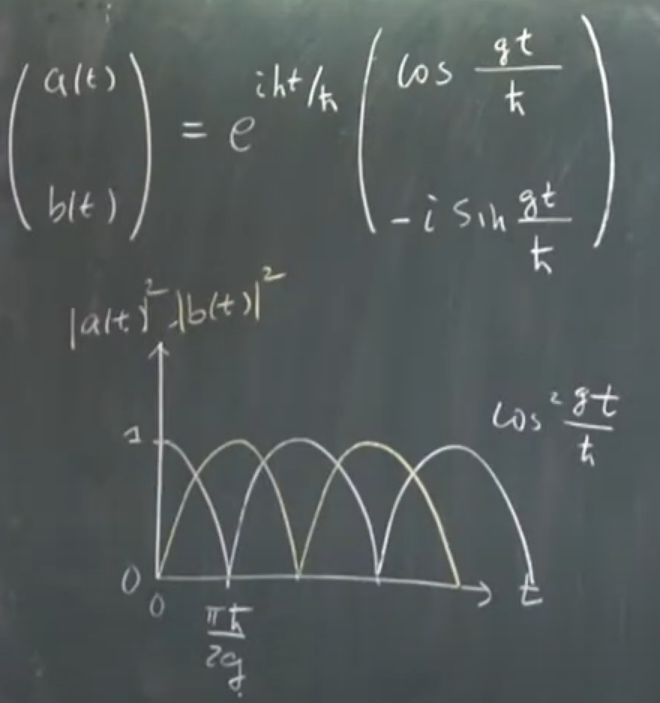系统在两个状态之间变换，或者说“振荡”。提出这个的初衷是为了解决微中子振荡的问题。

对于其他的两个状态的振荡系统，如果哈密顿量同样是\(H=\left(\begin{array}{ll} h & g \\ g & h \end{array}\right)  \)，那么对应的计算和我们上面的完全一样(比如研究电子的自旋，后面会讲)。
(1) 如果\(  g=0\)，那么哈密顿量就是一个对角矩阵，向量各自分量的状态不会变化，永远待在初始的状态，类似我们一阶线性微分方程组的解耦之后的状态；
(2) 如果\( g\neq 0 \)，那么就会在两种状态间切换，切换的速度(频率)由\( g \)的大小决定。
(3) \(  g\)值描述从一个state跳到另一个state的强度/能力，以后会叫作oscillator strength。\(  g\)值也是两个状态耦合的强度所对应的常数，耦合越强，状态之间相互转换越快；调控\(  g\)的大小，选择让两个状态相互作用(\(  g\)很大，用于量子计算)，或者保存某个状态的信息(\(  g\)很小，用于信息存储)。

上面的解法其实就是我们线性代数中求解\(\displaystyle\frac{d \mathbf{u}}{d t}=A \mathbf{u}  \)的方法，其中\(  \mathbf{u}\)是\(  u_1\)和\(  u_2\)组合成的向量，两个微分方程耦合在了一起，我们最终可以解出\(  \mathbf{u}(t)=c_{1} e^{\lambda_{1} t} \mathbf{x}_{1}+c_{2} e^{\lambda} 2^{t} \mathbf{x}_{2}\)，具体参见线性代数2。

谐振子的矩阵解释

谐振子定态方程为$$-\frac{\hbar^{2}}{2 m} \frac{d^{2} \psi}{d x^{2}}+\frac{1}{2} m \omega^{2} x^{2}=E \psi$$我们用梯度算符有$$\left\{\begin{array}{l} a_{+}|n\rangle=\sqrt{n+1}|n+1\rangle \\ a_{-}|n\rangle=\sqrt{n}|n-1\rangle \end{array}\right.$$最终结果为\(  |n\rangle=\displaystyle\frac{1}{\sqrt{n !}}\left(a_{+}\right)^{n}|0\rangle\)，这里的\( |0\rangle\ \)表示的是基态的波函数，是一个高斯分布的函数。我们的基底为\(  \{|n\rangle\}\)。$$\begin{aligned} (a_{+})_{m n} &=\langle m|a_{+}| n\rangle \\ &=\sqrt{n+1}\langle m|n+1\rangle \\ &=\sqrt{n+1} \delta_{m, n+1} \end{aligned}$$将上式左右两端写成矩阵有(根据\( \delta_{m, n+1} \)的特点，只有当行数比列数大\( 1 \)时才有非零元素，\(  H|n\rangle=E_{n}|n\rangle\))$$a_{+}|1\rangle=\sqrt{2}|2\rangle=\left(\begin{array}{cccc} 0 & 0 & 0 & 0 \\ \sqrt{1} & 0 & 0 & 0 \\ 0 & \sqrt{2} & 0 & 0 \\ 0 & 0 & \sqrt{3} & 0 \\ \vdots & \vdots & \vdots& \vdots& \ddots \end{array}\right)\left(\begin{array}{l} 0 \\ 1 \\ 0 \\ 0 \\ \vdots \end{array}\right)=\sqrt{2}\left(\begin{array}{l} 0 \\ 0 \\ 1 \\ 0 \\ \vdots \end{array}\right)$$这个矩阵的意思是上升算符作用在第一激发态，那么得到的是第二激发态和\(\sqrt{2}  \)的乘积。其中\(  \left(\begin{array}{ccccc} 0 & 0 & 0 & 0 \\ \sqrt{1} & 0 & 0 & 0 \\ 0 & \sqrt{2} & 0 & 0 \\ 0 & 0 & \sqrt{3} & 0 \\ \vdots & \vdots & \vdots & \vdots & \ddots \end{array}\right)\)表示上升算符\(  a_+\)，\( \left(\begin{array}{c} 0 \\ 1 \\ 0 \\ 0 \\ \vdots \end{array}\right) \)表示的是第一激发态(第二低的本征态)，同理\( \left(\begin{array}{c} 1\\ 0\\ 0 \\ 0 \\ \vdots \end{array}\right) \)表示的就是基态，\(  \left(\begin{array}{c} 0 \\ 0\\ 1 \\ 0 \\ \vdots \end{array}\right)\)表示的是第二激发态。

同样地，对于下降算符，我们有$$\begin{aligned} \left(a_{-}\right)_{m n} &=\left\langle m\left|a_{-}\right| n\right\rangle \\ &=\sqrt{n}\langle m | n-1\rangle \\ &=\sqrt{n} \delta_{m, n-1} \end{aligned}$$下降算符的矩阵表示为$$a_-=\left(\begin{array}{ccc} 0 & \sqrt{1} & 0 & 0 \\ 0 & 0 & \sqrt{2} & 0 \\ 0 & 0 & 0 & \sqrt{3} \\ 0 & 0 & 0 & 0 \\ \vdots &\vdots &\vdots &\vdots&\ddots \\ \end{array}\right)$$根据$$a_{\pm} \equiv \frac{1}{\sqrt{2 \hbar m \omega}}(\mp i p+m \omega x)$$于是$$x=\left(a_{+}+a_{-}\right) \cdot \frac{\sqrt{2 m \hbar \omega}}{2 m \omega}=\sqrt{\frac{\hbar}{2 m w}}\left(a_{+}+a_{-}\right)$$所以$$x=\sqrt{\frac{\hbar}{2 m w}}\left(\begin{array}{ccc} 0 & \sqrt{1} & 0 & 0 \\ \sqrt{1} & 0 & \sqrt{2} & 0 \\ 0 & \sqrt{2} & 0 & \sqrt{3} \\ 0 & 0 & \sqrt{3} & 0&\ddots \end{array}\right)$$同理可以得到$$p=i \sqrt{m \omega \hbar / 2}\left(\begin{array}{ccccc} 0 & -\sqrt{1} & 0 & 0 & \ldots \\ \sqrt{1} & 0 & -\sqrt{2} & 0 & \ldots \\ 0 & \sqrt{2} & 0 & -\sqrt{3} & \ldots \\ 0 & 0 & \sqrt{3} & 0 & \ldots \\ \vdots & \vdots & \vdots & \vdots & \ddots \end{array}\right)$$而哈密顿量\( H=\displaystyle\frac{p^{2}}{2 m}+\displaystyle\frac{1}{2} m w^{2} x^{2} \)，所以可以改写为下图，\(  \hbar \omega\)和中间那个大矩阵的乘积就是哈密顿算符\( H \)的矩阵表示，是将前面\( x \)和\(p \)的矩阵代入\( H=\displaystyle\frac{1}{2 m}\left[p^{2}+(m \omega x)^{2}\right] \)得到的。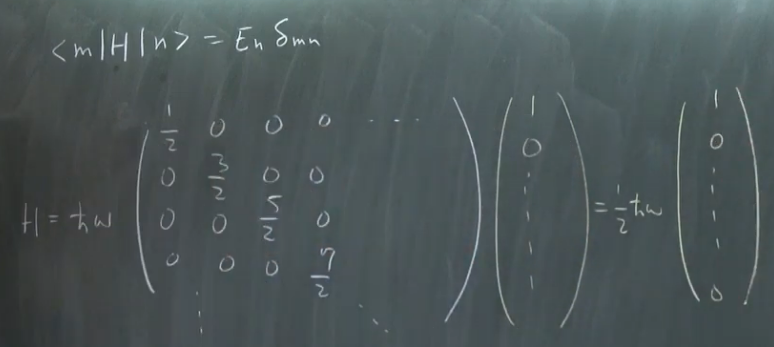$$H=\hbar \omega\left(\begin{array}{ccccc} \displaystyle\frac{1}{2} & 0 & 0 & 0 & \ldots \\ 0 & \displaystyle\frac{3}{2} & 0 & 0 & \ldots \\ 0 & 0 & \displaystyle\frac{5}{2} & 0 & \ldots \\ 0 & 0 & 0 & \displaystyle\frac{7}{2} & \ldots \\ \ldots & \ldots & \ldots & \ldots & \ldots \end{array}\right)$$上式表示哈密顿量作用在基态，提取出该态下的能量。
注意：
(1)  \( Q_{m n}=\left\langle e_{m}|\hat{Q}| e_{n}\right\rangle \)，我们不需要\(\hat{Q}  \)是哈密顿算符；
(2)  在\(a_-  \)算符中，第一行\( \begin{array}{lllll} 0 & \sqrt{1} & 0 & 0 \end{array} \)第二元素不为零，表示第一个状态和第二个状态之间存在耦合(coupling，或者interaction)，如果是处在对角线的元素不为零，那么这个元素背后没有任何任何耦合的含义'(从线性微分方程的角度很容易理解)。在半导体面，两个band之间的相互作用，就可以用这些非对角线上的元素来描述这种相互作用interaction term。

Pages: 1 2 3 4 5 6 7 8 9

Leave a Reply