自由粒子
Eigen state和真正存在的state
自由粒子即势能处处为零\( V(x)=0 \)，在经典角度来看，就是没有外力作用了，那么物体将匀速直线运动，量子力学中则不一样，和一维无线深势阱(不考虑边界势场)一样有方程$$-\frac{\hbar^{2}}{2 m} \frac{d^{2} \psi}{d x^{2}}=E \psi$$令\(k \equiv \displaystyle\frac{\sqrt{2 m E}}{\hbar} \)，则方程为$$\frac{d^{2} \psi}{d x^{2}}=-k^{2} \psi$$一般解为$$\psi(x)=A e^{i k x}+B e^{-i k x}$$没有边界条件去限制\( k\)或者说\(E \)(a free particle can carry any energy，量子力学并不是所有的情况能量都是quantize的)，当然能量必须取正值。将时间因子\(\exp (-i E t / \hbar) \)代入有(用波矢去改写这个时间项)$$\Psi(x, t)=A e^{i k\left(x-\frac{\hbar k}{2 m} t\right)}+B e^{-i k\left(x+\frac{\hbar k}{2 m} t\right)}$$前面一项表示波向正轴方向传播，后一项表示往负轴方向传播(能量相同)，如果我们允许\( k \)取负值，其实就涵盖了这两项。$$k \equiv \pm \frac{\sqrt{2 m E}}{\hbar}, \quad\left\{\begin{array}{l} k>0 \Rightarrow \text { 向右传播 } \\ k<0 \Rightarrow \text { 向左传播. } \end{array}\right.$$那么方程的解可以改写为$$\Psi_{k}(x, t)=A e^{i\left(k x-\frac{\hbar k^{2}}{2 m} t\right)}$$注：波动方程写成复指数的形式为\( y=A e^{i(k x-\omega t)} \) 波长为\( \lambda=2 \pi /|k| \)，动量为\(p=\hbar k \)，波的速度，或者说【相速度】phase velocity为$$ v_{\text {量子 }}=\frac{ \omega }{ k }=\frac{\hbar|k|}{2 m}=\sqrt{\frac{E}{2 m}} $$另一方面，对一个没有势能只有动能的物体的速度可以表示为$$v_{\text {经典}}=\sqrt{\frac{2 E}{m}}=\frac{\hbar|k|}{m}=2 v_{\text {量子}}$$表面上看量子力学的波的传播速度只有粒子经典速度的一半！
如果不考虑时间因子，或者说让\( t=0 \)，我们很容易发现$$\int_{-\infty}^{\infty} \Psi_{k}^{*} \Psi_{k} d x=|A|^{2} \int_{-\infty}^{\infty} d x=|A|^{2}(\infty)$$即不满足归一化条件！因为不能归一化，所以不是一个真实的物理的state。
老师上课用的是\(\psi \)，即证明\(\displaystyle\int_{-\infty}^{+\infty} \psi_{k}^{*}(x) \psi_{k}(x) d x=|A|^{2} \displaystyle\int_{-\infty}^{+\infty} e^{-i k x} \cdot e^{+i k x} d x\)不可归一化，即eigenfunction of a free particle is not normalizable!也就是说不能单纯地待在free particle 的eigen state。前面讨论的无线深势阱或者谐振子模型中，即\(\psi=\displaystyle\sum_{n} c_{n} \psi_{n} \)，待在\( \psi_{n} \)的线性组合或者直接待在\( \psi_{i}\)(\( c_{i}=1\)，其他系数都为零)都是allowed。但是对于free particle来说，只能待在连续线性组合(能保证归一化)，而不能待在某一个特定的eigen state\(\psi_{n} \)。设想如果真的待在某一个特定的\(\psi_{n} \)，那么测不准原理就失效了。
真正存在的state为$$\Psi(x, t)=\frac{1}{\sqrt{2 \pi}} \int_{-\infty}^{\infty} \phi(k) e^{i\left(k x-\frac{\hbar k^{2}}{2 m} t\right)} d k$$其中\( \phi(k) \)对应于以前的\(c_{n} \)，或者说频域的函数大小(对应于频率\(k \))，求和符号变为积分符号。初始条件$$\Psi(x, 0)=\frac{1}{\sqrt{2\pi}} \int_{-\infty}^{+\infty} \phi(k) e^{i k x} d k$$于是系数(这里的基为\(e^{-i k x}\))$$\phi(k)=\frac{1}{\sqrt{2 \pi}} \int_{-\infty}^{+\infty} \Psi(x, 0) e^{-i k x} d x$$
注：傅里叶逆变换和傅里叶变换(位置空间和波矢/动量空间转换)$$\begin{array}{l} f(x)=\displaystyle\frac{1}{\sqrt{2 \pi}} \int_{-\infty}^{+\infty} F(k) e^{i k x} d k \\ F(k)=\displaystyle\frac{1}{\sqrt{2 \pi}} \int_{-\infty}^{+\infty} f(x) e^{-i k x} d x \end{array}$$
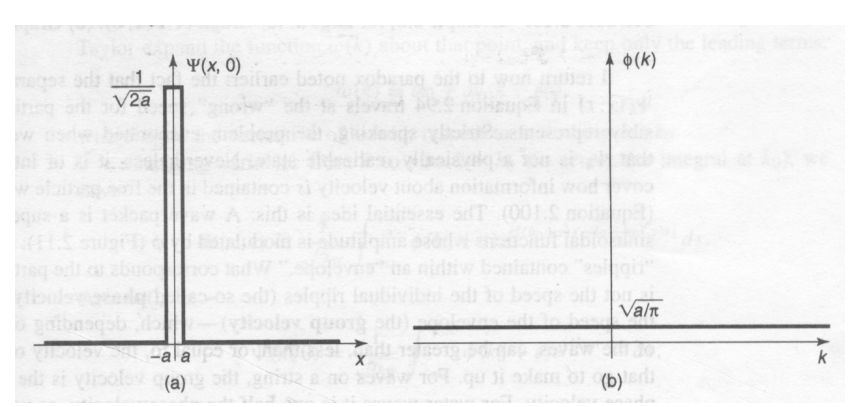下面给定一个初始条件\(\Psi(x, 0)\)如上图，即free particle待在原点附近，对应于上面左侧的图，这里的\(a\)很小。(注意上面右侧的图对应的是\(a\)无限小的情况)$$\Psi(x, 0)=\left\{\begin{array}{cl} \displaystyle\frac{1}{\sqrt{2 a}} & -a<x<a \\ 0 & \text { otherwise } \end{array}\right.$$注意这里\( \Psi(x, 0)^2 \)和\(x \)轴的面积为1，满足初始化的归一条件。
\( k\)的分布其实是动量的分布，因为\( \hbar k \)是动量，而\( \hbar\)为常数。\( k \)的分布(反变换)为$$\begin{aligned} \phi(k) &=\frac{1}{\sqrt{2 \pi}} \frac{1}{\sqrt{2 a}} \int_{-a}^{a} e^{-i k x} d x=\left.\frac{1}{2 \sqrt{\pi a}} \frac{e^{-i k x}}{-i k}\right|_{-a} ^{a} \\ &=\frac{1}{k \sqrt{\pi a}}\left(\frac{e^{i k a}-e^{-i k a}}{2 i}\right)=\frac{1}{\sqrt{\pi a}} \frac{\sin (k a)}{k} \end{aligned}$$所以波函数的解为$$\Psi(x, t)=\frac{1}{\pi \sqrt{2 a}} \int_{-\infty}^{\infty} \frac{\sin (k a)}{k} e^{i\left(k x-\frac{\hbar k^{2}}{2 m} t\right)} d k$$不能积成一个基本函数，只能通过数值积分计算。事实上，除了少数情况外，大部分情况下\( \Psi(x, t)\)都不能积成一个基本函数。
讨论波矢空间\( \phi(k)\)的图像
我们已经知道$$\phi(k)=\frac{1}{\sqrt{\pi a}} \frac{\sin (k a)}{k}$$(1) 当\(a \)很小，即初始给定的粒子运动空间很小，那么\( \sin (k a) \approx k a\)，因此有$$\phi(k) \approx \sqrt{\frac{a}{\pi}}$$这是不确定性原理的一个典型例子：位置坐标弥散很小，那么动量必定弥散很大。(下图的黄色线条是\(\phi(k)\)最终的样子，其实就是\(\text{sinc} \)函数的模样)$$a \downarrow, \sigma_{x} \downarrow, \sigma_{p} \uparrow$$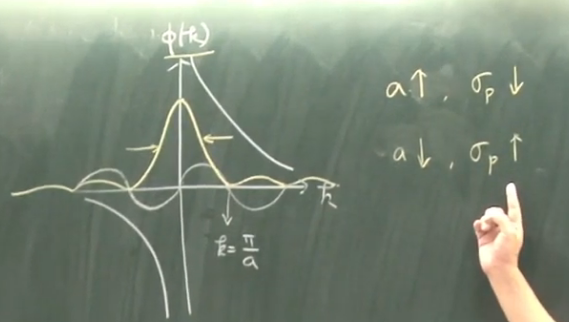
(2) 当\(a \)很大时，位置坐标弥散很大，动量弥散很小。$$a \uparrow, \sigma_{x}\uparrow,\sigma_{p} \downarrow$$
群速度和相速度
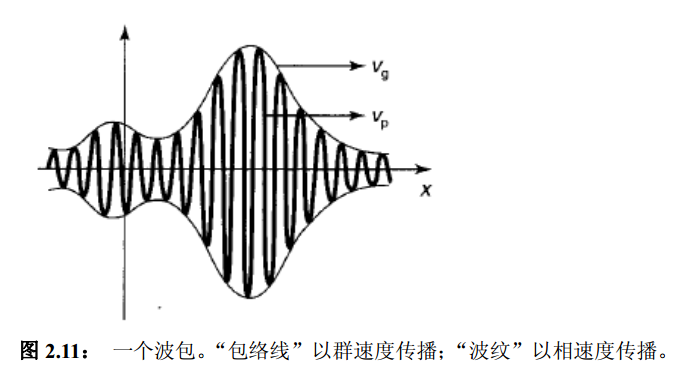
- 【群速度】
- \(v_{\text {群 }}=\displaystyle\frac{d \omega}{d k}\)，就是经典的速度，比如经典物理，我们说一个物体的运动速度，其实就是群速度；
- 波包的速度也是群速度；
- 粒子的速度不是单个ripples的速度(即相速度)，而是envelope的速度(群速度)
- 群速度的大小取决于the nature of the waves，可以比相速度更大、更小或者相等。
- 【波包】
- (wavepacket)是局限在空间的某有限范围区域内的波动，在其他区域的部分非常微小，可以被忽略；
- 波包是 a superposition of sinusoidal functions whose amplitude is modulated by \(\phi(k)\).
- 波包consists of “ripples” contained within an “envelope”.
- 【相速度】
- \(v_{\text {相 }}=\displaystyle\frac{\omega}{k}\)
- 单个ripples的速度就是相速度，在传播过程中，这个ripple的振幅会有变化，但是相位不变。
- 群速度/相速度实例
- 对于string上的波，群速度等于相速度(不考虑刚度)，参考MIT振动与波；
- For water waves it is one-half the phase velocity, as you may have noticed when you toss a rock into a pond (if you concentrate on a particular ripple, you will see it build up from the rear, move forward through the group, and fade away at the front, while the group as a whole propagates out at half that speed).
这里说的是deep water gravity waves，\(\omega=\sqrt{g k}\)，因此\(v_{\mathrm{g}}=v_{\mathrm{p}} / 2\) - 对于量子力学中的自由粒子，群速度是相速度的两倍，just right to match the classical particle speed.
- 对于string上的波，群速度等于相速度(不考虑刚度)，参考MIT振动与波；
Wave packet velocity
Consider the "wave packet" \(\Psi(x, t)=e^{i\left(k_{1} x-\frac{\hbar k_{1}^{2}}{2 m} t\right)}+e^{i\left(k_{2} x-\frac{\hbar k_{2}^{2}}{2 m} t\right)}\)，这里\(k_{2} \)和\(k_{2} \)很接近，其实就是两个波的频率很接近，令$$\begin{aligned} &\alpha \equiv \frac{k_{1}+k_{2}}{2} x-\frac{\hbar\left(k_{1}^{2}+k_{2}^{2}\right)}{4 m} t \\ &\Delta \equiv \frac{k_{1}-k_{2}}{2} x-\frac{\hbar\left(k_{1}^{2}-k_{2}^{2}\right)}{4 m} t \end{aligned}$$那么wave packet的函数可以改写为$$\Psi(x, t)=e^{i(\alpha+\Delta)}+e^{i(\alpha-\Delta)}=e^{i \alpha}\left(e^{i \Delta}+e^{-i \Delta}\right)=e^{i \alpha} 2 \cos (\Delta)$$我们前面说了\(k_{2} \)和\(k_{2} \)很接近，所以\( \Delta\) evolves much more slowly with space and time than \(\alpha \)，对应于下图中的slowlying varying envelope，而\(\alpha \)对应于下图的快速变化的部分。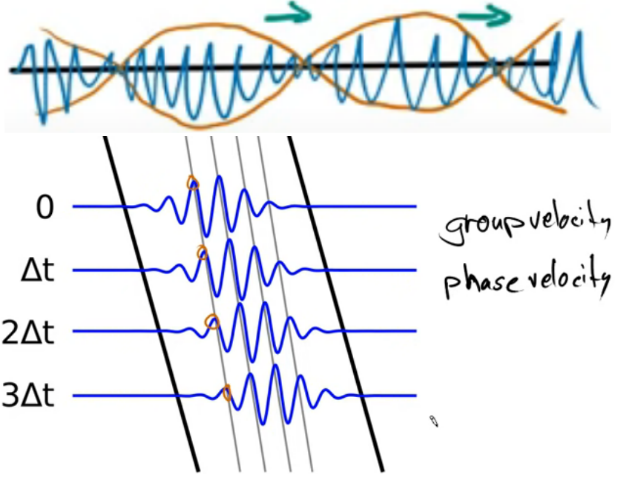
【色散关系】
前面讨论的波函数的解为\(\Psi_{k}(x, t)=A e^{i\left(k x-\frac{h k^{2}}{2 m} t\right)} \)，其中\( \omega=\left(\hbar k^{2} / 2 m\right) \)即为角频率\(\omega \)和波矢\( k\)的关系，又叫“色散关系”，这里的角频率除以波矢即为传播速度，显然和波矢有关。其实类似让一束混色光从介质的一端垂直射入，然后在介质中沿着直线传播，在介质的另一端垂直射出，由于不同颜色的光在介质中的传播速度不同，因此虽然不同颜色的光都是从同一点同一时刻从一段射入的，但是在出口段会在不同的时刻接收到不同颜色的光。
事实上，对于任何形式的色散关系，如果\( \phi(k)\)是\( k _{0}\)附近的一个窄分布(类似单色性好的激光的波矢大小分布)，于是我们可以在\( k _{0}\)处进行一阶展开(线性近似)。得到$$\omega(k) \cong \omega_{0}+\omega_{0}^{\prime}\left(k-k_{0}\right)$$将变量由\( k \)变为\(s \)，即\( s \equiv k-k_{0}\)，使得积分区间中心在\( k_{0} \)，于是波函数可以表示为$$\begin{aligned} \Psi(x, t) & \approx \frac{1}{\sqrt{2 \pi}} \int_{-\infty}^{+\infty} \phi\left(k_{0}+s\right) e^{i\left[\left(k_{0}+s\right) x-\left(\omega_{0}+\omega_{0}^{\prime} s\right) t\right]} d s \\ &=\frac{1}{\sqrt{2 \pi}} e^{i\left(k_{0} x-\omega_{0} t\right)} \int_{-\infty}^{+\infty} \phi\left(k_{0}+s\right) e^{i s\left(x-\omega_{0}^{\prime} t\right)} d s \end{aligned}$$上式最后写成的是不含\(s\)的积分外的项和含有\(s\)的积分项的乘积。The term in front is a sinusoidal wave (the "ripples"), traveling at speed \(\omega_{0} / k_{0}\). It is modulated by the integral (the "envelope"), which is a function of \(x-\omega_{0}^{\prime} t\), and therefore propagates at the speed \(\omega_{0}^{\prime}\).$$\begin{array}{c} v_{\text {群 }}=\omega_{0}^{\prime}=\displaystyle\frac{d \omega}{d k}=\frac{d(E / \hbar)}{d(p / \hbar)}=\frac{d\left(p^{2} / 2 m\right)}{d p}=\displaystyle\frac{p}{m}=\hbar k/m=v_{\text {经典 }} \\ v_{\text {相 }}=\displaystyle\frac{\omega}{k}=\hbar k / 2 m =v_{\text {群 }}/2\end{array}$$
补充1：\( \omega \)在物理学中常见的两种含义，“角频率”(Angular frequency)和“角速度”(Angular velocity)区别是什么？
答：
角频率和角速度的百区别究竟是：
1、研究范围不一样：角频率是在任度意的周期性运动中。角速度是在圆周运动中，或者至少是瞬时的圆周运动中。
2、物理意义不一知样：角频率是单位时间内的振动次道数与\( 2\pi \)之积。一个以弧度为单位的圆，在单位时间内内所走的弧度即为角速度。
3、计算方法不一样：角频率的计算公式是\( \omega =\displaystyle\frac { 2\pi}{ T } \)。角速容度的计算公式为\( \omega = \displaystyle\frac { v }{r } \)，其中\( v \)为某时刻的线速度。补充2：德布罗意波$$\left\{\begin{array}{l} p=\hbar k \\ E=\hbar \omega \end{array}\right.$$
δ函数势
束缚态/散射态/δ函数简介
在处理固体物理或者半导体物理中，如果\( \Delta x \)或者\( \Delta p \)的变化率都很小，那么我们可以用经典的方法去处理。我们常说的semi-classcial指的是用量子力学的方法处理能带，剩下的都用古典的方式去想像(波包)。
\(\delta\)函数特点概述：
- \(\delta\)不是严格意义上的函数，而是“泛函”，函数的极限；
- 最大的用处是\(\displaystyle\int_{-\infty}^{+\infty} \delta(x-a) f(x) d x=f(a)\)
- \(\delta\) function of a function
\(\displaystyle\int_{-\infty}^{\infty} \delta(g(x)) f(x) d x=\displaystyle\delta(g(x))=\sum_{i} \displaystyle\frac{\delta\left(x-x_{i}\right)}{\left|g^{\prime}\left(x_{i}\right)\right|}\)，其中\(x_{i}\)为\(g(x)=0\)的地方
- Derivatives of \(\delta\)-functions
\(\displaystyle\int_{-\infty}^{\infty} \frac{d \delta(x)}{d x} f(x) d x=-\displaystyle\int_{-\infty}^{\infty} \delta(x) \frac{d f(x)}{d x} d x=\left.\displaystyle\frac{d f}{d x}\right|_{x=0}\) - 傅里叶变换：
- \(F(k)=\displaystyle\frac{1}{\sqrt{2 \pi}} \int_{-\infty}^{\infty} \delta\left(x-x_{0}\right) e^{-i k x} d x=\frac{1}{\sqrt{2 \pi}} e^{-i k x_{0}}\)
- \( f(x)=\displaystyle\frac{1}{\sqrt{2 \pi}} \int_{-\infty}^{\infty} \frac{1}{\sqrt{2 \pi}} e^{-i k x_{0}} e^{i k x} d k =\frac{1}{2 \pi} \int_{-\infty}^{\infty} e^{i k\left(x-x_{0}\right)} d k=\delta\left(x-x_{0}\right)\)
假设\(x-x_{0}\neq 0\)，随着\(k\)的变化，积分项函数在复平面上旋转，或者想象成沿着\(k\)的三维空间旋转前进，所以其积分结果随着取值范围的变化是在不断振荡的，如果积分区间取正负无穷，那么根据对称性，我们可以"感觉"最终的积分值还是为零(结论是对的，但是需要更严谨的数学推导)。 - 最简单的情形是\(\delta(x)=\displaystyle\frac{1}{2 \pi} \int_{-\infty}^{+\infty} e^{i k x} d k\)，\(\mathcal{F} f(k)=1\)，严格推导参见分布的傅里叶变换或这里；
-
非严格数学推导：$$ \int_{-a}^{a} e^{i k x} d k=\left.\frac{e^{i k x}}{i x}\right|_{-a} ^{a}=\frac{e^{i x a}-e^{-i x a}}{i x}=\frac{2 i \sin x a}{i x}=2 a \frac{\sin x a}{x a} $$如果 \(a \rightarrow \infty\) ，那么这里的\(\sin xa\)快速振荡：(满足下面三点，因此就说明是\(\delta(x)\)）
- 当\(x = 0\)时，\(\displaystyle\int_{-a}^{a} e^{i k x} d k\)显然为无穷大；
- 当\(x \neq 0\)时，函数从\(x=0\)点快速向\( x\)正负轴衰减到零，对应于\(x=\pm \displaystyle\frac{\pi}{a}\)两点，在这两点包含的数轴空间外，函数可以近似认为零，而\(a \rightarrow \infty\)，所以极限情况，函数非零区间只有\(x=0\)；
- 对函数积分其实就是对\(x=\pm \displaystyle\frac{\pi}{a}\)两点包含的三角形进行积分，底为\(\displaystyle\frac{2 \pi}{a}\)，高为\(1\)，所以面积为 \(\displaystyle\frac{\pi}{a}\)，于是\( \displaystyle\int_{-\infty}^{+\infty}(\frac{1}{2 \pi} \int_{-\infty}^{+\infty} e^{i k x} d k)dx =0\)
薛定谔方程的两类解：
- 束缚态(bound state)
例子：一维无线深势阱，谐振子(\(\psi_{k}(x)=A e^{-i k x} \))。eigenstate在\( x \)无穷大的地方，必为零。 - 散射态(scattering state)
例子：free particle (\(\psi_{k}(x)=A e^{i k x} \))。eigenstate在\( x \)无穷大的地方，不趋近于零。
求解束缚态(\(E<0\))
我们现在要求的是势场为\(V(x)=-\alpha \delta(x) \quad(\alpha>0) \)，总能量\(E<0 \)，即束缚态的波函数解。$$-\frac{\hbar^{2}}{2 m} \frac{d^{2} \psi}{d x^{2}}-\alpha \delta(x) \psi=E \psi$$对于非边界区(\( x<0 \)的区域和\( x>0 \)的区域)，\( V(x)=0 \)$$\frac{d^{2} \psi}{d x^{2}}=-\frac{2 m E}{\hbar^{2}} \psi=\kappa^{2} \psi$$其中\(\kappa \equiv \displaystyle\frac{\sqrt{-2 m E}}{\hbar}\)为正实数，微分方程的一般解为$$\psi(x)=A e^{-\kappa x}+B e^{\kappa x}$$为了不让波函数爆掉，必然有：
- \( x<0 \)的区域，\(A=0\)；
- \( x>0 \)的区域，\(B=0\)；
根据前面的章节(波函数形状和连续性讨论)，我们知道：
- \(\psi\)任意处都必须是连续的；
- \(d \psi / d x\)任意处都必须是连续的，除非某处的势函数无穷大；
根据第一条我们推出\(A=B\)，下面重点讨论第二条。\(\delta\) functions are only really meaningful when you treat them as distributions and integrate. 这里我们将等式两边从\(-\varepsilon \)积分到\(+\varepsilon\)，然后让\( \varepsilon \)无线趋近于零\(\varepsilon \rightarrow 0 \)，于是有$$-\frac{\hbar^{2}}{2 m} \int_{-\varepsilon}^{\varepsilon} \frac{d^{2} \psi}{d x^{2}} d x-\alpha \int_{-\varepsilon}^{\varepsilon} \delta (x) \psi(x) d x=E \int_{-\varepsilon}^{\varepsilon} \psi(x) d x$$极限情况等式右边为零，于是上式可以化为$$-\left.\frac{\hbar^{2}}{2 m} \frac{d\psi}{d x}\right|_{-\epsilon} ^{\epsilon}-\alpha \psi(0)=0$$进一步化简得到$$ \left.\frac{d^{2} \psi}{d x}\right|_{-\epsilon} ^{\epsilon}=\frac{-2 m \alpha }{\hbar^{2}} \psi(0) $$波函数连续性要求很容易求得\(\psi(0)=B\)，然后将之前得到的波函数左右两侧的表达式代入上式得到\(-B K-B K=-\displaystyle \frac{2 m \alpha }{\hbar^{2}} B\)，于是\(\kappa=\displaystyle\frac{m \alpha}{\hbar^{2}}\)。
允许的能量值$$E=-\frac{\hbar^{2} \kappa^{2}}{2 m}=-\frac{m \alpha^{2}}{2 \hbar^{2}}$$归一化波函数取正根得到\(B=\sqrt{\kappa}=\displaystyle\frac{\sqrt{m \alpha}}{\hbar}\)
无论这里的强度\( \alpha\)多大，每个\( \alpha\)对应的束缚态解只有唯一解。\( \alpha \)越大，这个\( E \)越深，负得越多，eigenstate decay得越快。$$\psi(x)=\frac{\sqrt{m \alpha}}{\hbar} e^{-m \alpha|x|/ \hbar^{2}} ; \quad E=-\frac{m \alpha^{2}}{2 \hbar^{2}}$$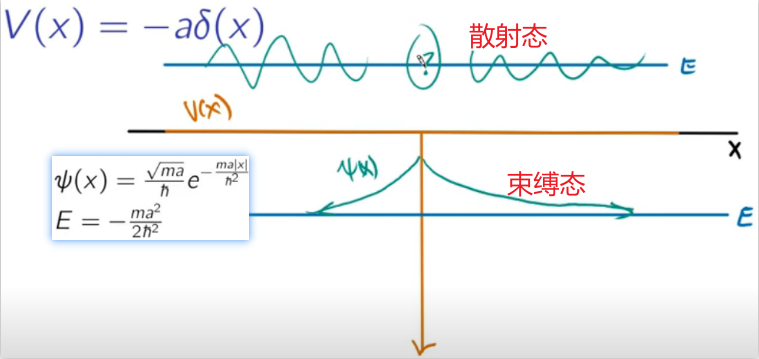
求解散射态(\(E>0\))
对于散射态，我们通常不求解wave function和eigen energy，而是解能和实验上相对照的东西(发展理论需要)，比如transmission probability。
例子：卢瑟福散射实验，\( \alpha \)粒子打到金箔上，多少比例的会穿过，多少比例会回弹。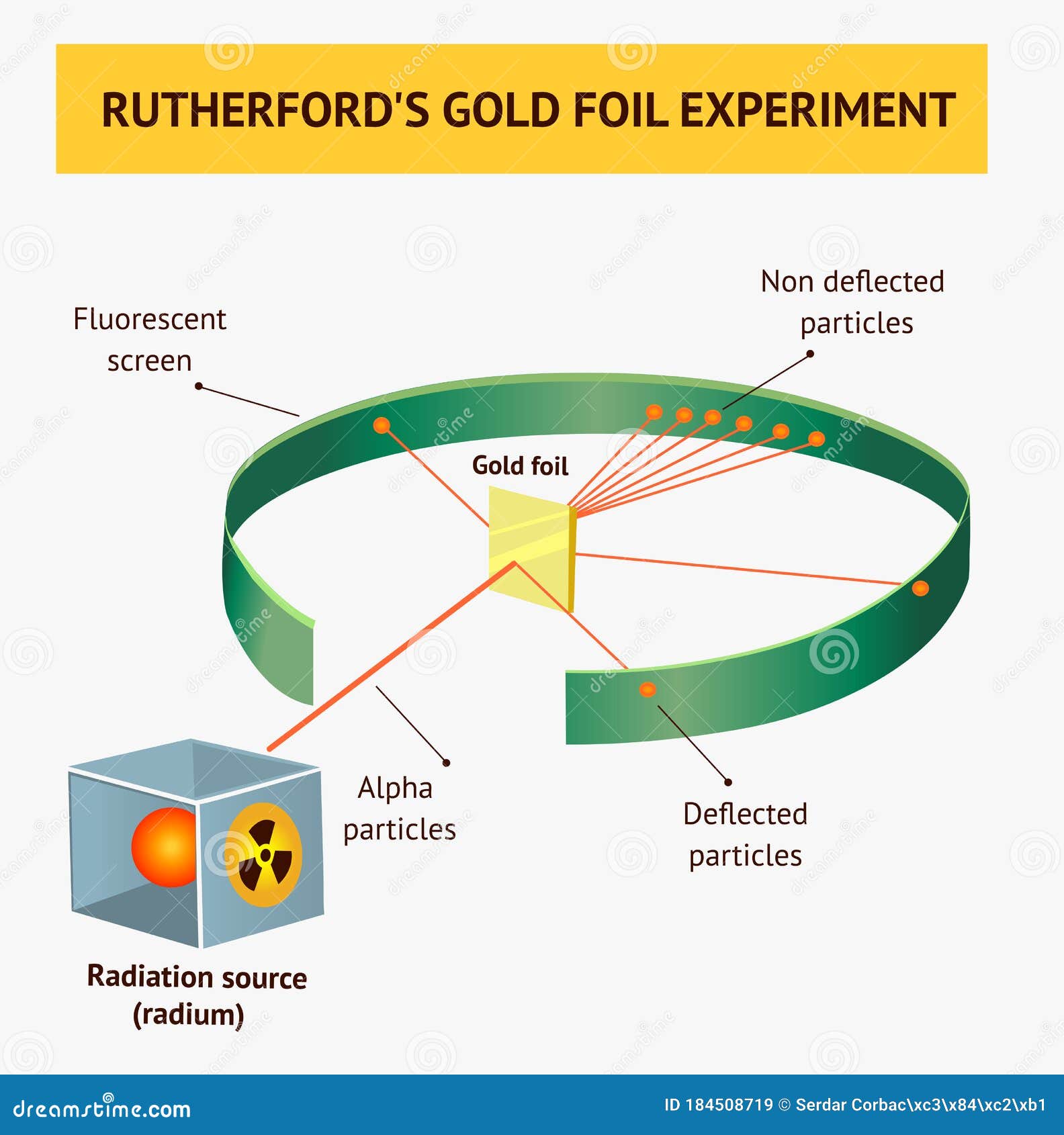
(a) 子弹从左边射过来，地上有一个坑，那么子弹运动到坑附近可能会反弹。这种思考方式会很奇怪，不容易理解。
(b) 不同位置具有不同的势能，也就具有不同的波数\( k\)值，即物质波的波长会改变。从电磁学的角度来看，等效为一个不同的折射率\( n \)的材料突然出现，所以波长发生变化，而且原来的波会有部分是透射，部分是反射。
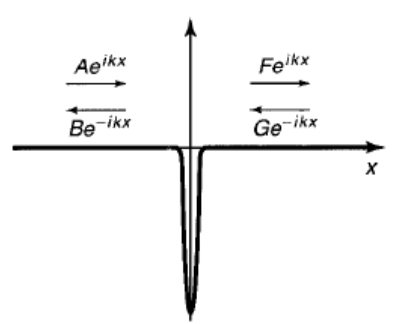\(E=\displaystyle\frac{\hbar^{2} k^{2}}{2 m} \quad k=\displaystyle\frac{\sqrt{2 m E}}{\hbar} \) 方程的解(都看成是free particle，只存在透射和反射，所以\(G=0\))$$\left\{\begin{array}{ll} x<0, & \psi(x)=A e^{i k x}+B e^{-i k x} \\ x>0, & \psi(x)=F e^{i k x} \end{array}\right.$$根据我们前面讨论的边界条件有$$\begin{array}{c} \psi\left(0^{+}\right)=\psi\left(0^{-}\right) \Rightarrow A+B=F \\ i k A-i k B-i k F=\frac{-2 m \alpha}{\hbar^{2}}(A+B) \end{array}$$现在穿过去的几率和反射回来的几率为(只需要求比值)$$\left\{\begin{array}{l} T(E)=\displaystyle\frac{|F|^{2}}{|A|^{2}} \\ R(E)=\left|\displaystyle\frac{B}{A}\right|^{2} \end{array}\right.$$很容易根据前面的方程组(三个未知数，两个方程)求得上述比例为$$\begin{aligned} &B=\frac{i \beta}{1-i \beta} A\\ &F=\frac{1}{1-1 \beta} A \end{aligned}$$其中\( \beta \equiv \displaystyle\frac{m \alpha}{\hbar^{2} k} \)，求得$$\begin{aligned} &R=\left|\frac{B}{A}\right|^{2}=\frac{i \beta \cdot(-i \beta)}{(1-i \beta)(1+i \beta)}=\frac{\beta^{2}}{1+\beta^{2}}==\frac{1}{1+\frac{2 \hbar^{2} E}{m \alpha^{2}}}\\ &T=\left|\frac{F}{A}\right|^{2}=\frac{1}{1+\beta^{2}}=\frac{1}{1+\frac{m \alpha^{2}}{2 \hbar^{2} E}} \end{aligned}$$稍微检验一下发现\( R+T=1 \)，对的。根据\( \beta \equiv \displaystyle\frac{m \alpha}{\hbar^{2} k}\)和\( E=\displaystyle\frac{\hbar^{2} k^{2}}{2 m}\)可以将上面的结果改写成和\(E \)有关的形式。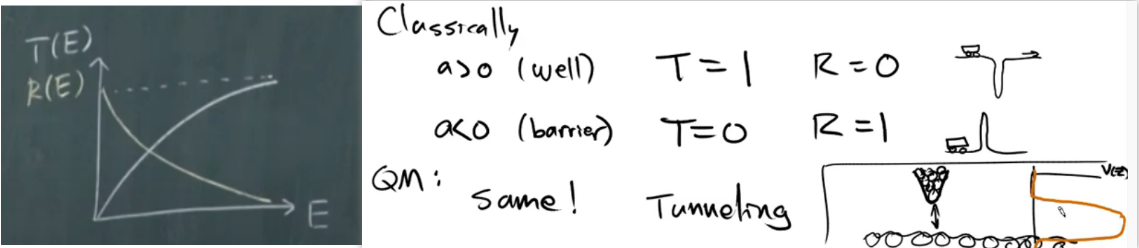
- 能量\( E \)越大，越表现出classcial的特性，就会看不到这里的potential，就如上面子弹的例子，真实情况是子弹肯定不会因为地上的坑而反弹；
- 能量\( E \)越小，越表现出量子力学的特性，反弹的比例越高；
- \( \alpha \)越大，坑越深，量子效应越明显，反射回来越多；
- 如果这里的\( a\)为负值，那么就是一个barrier，而不是上面讨论的well，但是最终的结果(\(R\)和\(T\)的值)不会变化。但是如果从classcial的观点看，barrier和well的结果会完全不同。
有限深方势阱
$$V(x)=\left\{\begin{array}{ll} -V_{0}, & -a<x<a \\ 0, & |\mathrm{x}|>a \end{array}\right.$$其中的\(V_{0} \)是正数，同前面的\(\delta \)函数势阱一样，这里同样存在束缚态(\( E<0 \))以及散射态(\( E>0 \))，下面分开讨论。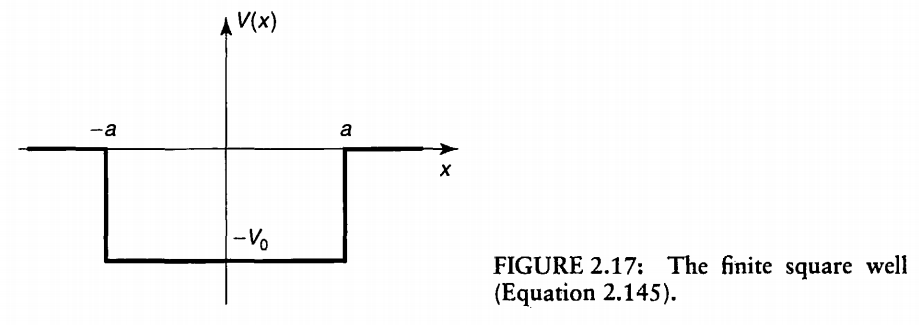
(a) 束缚态，\( 0>E>-V_{0} \)
分析可知，我们需要利用在\( x=a \)和\( x=-a \)两个地方的连续性和一阶导数的形式，写出临界条件方程，然后求解各个波函数。下面将分成三个区域讨论：
(1) \( x<-a \)区域$$-\frac{\hbar^{2}}{2 m} \frac{d^{2} \psi}{d x^{2}}=E \psi, \quad \text { 或 } \quad \frac{d^{2} \psi}{d x^{2}}=\kappa^{2} \psi$$其中\( \kappa \equiv \displaystyle\frac{\sqrt{-2 m E}}{\hbar} \)方程的解为\(\psi(x)=A \exp (-\kappa x)+B \exp (\kappa x) \)为了避免爆掉，允许的解为$$\psi(x)=B \exp (\kappa x), \quad x<-a$$(2) \( x>a \)区域，用同样地方法，我们可以得到解为$$\psi (x)=F e^{-k x}$$(3) \( -a<x<a \)区域$$-\frac{\hbar^{2}}{2 m} \frac{d^{2} \psi}{d x^{2}}-V_{0} \psi=E \psi, \quad \text { 或 } \quad \frac{d^{2} \psi}{d x^{2}}=-l^{2} \psi$$其中\( l \equiv \displaystyle\frac{\sqrt{2 m\left(E+V_{0}\right)}}{\hbar}\)(注意\( l\)必为正实数)，这里特征方程的解是实数(无阻尼弹簧振子模型)，那么我们就直接用正余弦函数线性组合表示解为$$\psi(x)=C \sin (l x)+D \cos (l x)$$
根据临界条件列方程组
(1) \( x=-a \)处$$\begin{aligned} B e^{-\kappa a} &=-C \sin l a+D \cos l a \\ \kappa B e^{-\kappa a} &=l C \cos l a+l D \sin l a \end{aligned}$$(2) \( x=a \)处$$\begin{aligned} F e^{\kappa a} &=C \sin l a+D \cos l a \\-\kappa F e^{\kappa a} &=l C \cos l a-l D \sin l a \end{aligned}$$势场是偶函数，所以类似前面的例子(谐振子或者一维无限深势阱)，它的解函数也应该是偶函数和奇函数交替，注意这是我们偷懒来猜的，当然这也是对的。其实严格来说，联立上面四个公式也可以得到结果。
先解even solution的情况，那么\( C=0\)
很容易看出$$ \kappa=l \tan l a $$因为\(\kappa \)和\(l \)都是和能量\(E \)有关的函数，所以都用\( E \)代换可以求得能量\(E \)，只能用绘图法求解。令$$z \equiv l a, \quad \text { 及 } \quad z_{0} \equiv \frac{a}{\hbar} \sqrt{2 m V_{0}}$$根据\( \left(\kappa^{2}+l^{2}\right)=2 m V_{0} / \hbar^{2}\)知道$$(\kappa a)^{2}+(l a)^{2}=z_{0}^{2} \quad \kappa a=\sqrt{z_{0}^{2}-z^{2}}$$而\( \kappa a=l a \tan l a \)，所以最终结果是$$\tan z=\sqrt{\left(z_{0} / z\right)^{2}-1}$$讨论一下\( z_{0} \)对解的影响：
(1)当陷阱很宽或者很深的时候，\( z_{0} \)很大，那么相交的解越来越多。其实很深的话，就可以极限到无线深位能阱，那么有无数解；深度不变的情况下，越宽的话，就是quantum confine越不强，相邻允许能态之间靠得越近，回到古典的case。
(2) 无论阱多浅多窄，至少有一个解。
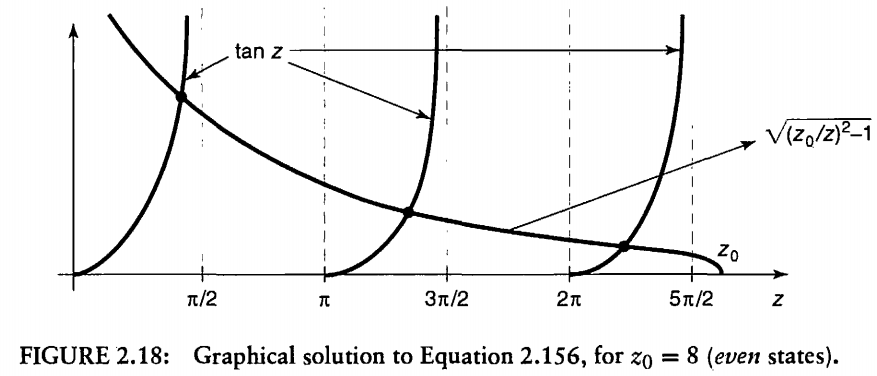odd solution的情况，那么\( D=0\)
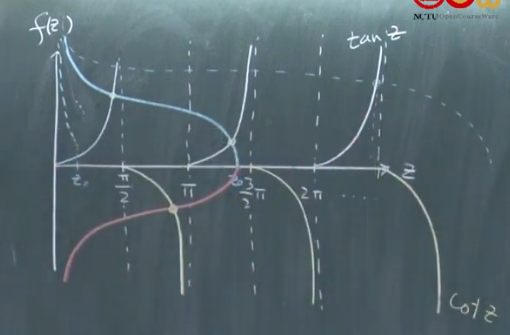同样地方法，有$$\cot z=-\sqrt{\left(\frac{z_{0}}{z}\right)^{2}-1}$$奇函数和偶函数的情况汇总，我们发现，可以通过调控\( z_{0}\)，可以得到一个eigenstate解、两个eigenstate解、三个eigenstate解、四个eigenstate解.......也就是可以控制量子阱中到底有几个state。简单分析也可以知道，对于不同的能级来说，隧穿到外面的比例也不同，能级越高越往外扩散(隧穿效应越明显)，能级越低越表现出localized的特性。
(b) 散射态，\(E>0 \)
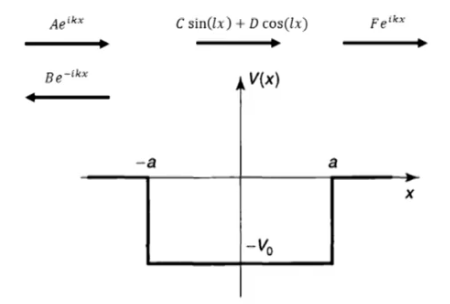(1) \( x<-a \)区域$$\psi(x)=A \mathrm{e}^{i k x}+B \mathrm{e}^{-i k x}$$其中\( k=\displaystyle\frac{\sqrt{2 m E}}{\hbar}\)
(2) \( -a<x<a \)区域，\( V(x)=-V_{0} \)$$\psi(x)=C \sin (l x)+D \cos (l x)$$其中\( l \equiv \displaystyle\frac{\sqrt{2 m\left(E+V_{0}\right)}}{\hbar}\)
(3) \( x>a \)区域
假设没有入射波，都是从左侧入射波入射，然后透射过势阱之后得到的波，于是为$$\psi(x)=F e^{i k x}$$\( A \)为入射波振幅，\(B \)为反射波振幅，\( F\)为透射波振幅。同样的四个临界条件(两个波函数连续，两个一阶导数连续)：$$\begin{array}{c} A e^{-i k a}+B e^{i k a}=-C \sin (l a)+D \cos (l a) \\ C \sin (l a)+D \cos (l a)=F e^{i k a} \\ i k\left[A e^{-i k a}-B e^{i k a}\right]=l[C \cos (l a)+D \sin (l a)] \\ l[C \cos (l a)-D \sin (l a)]=i k F e^{i k a} \end{array}$$消去\(C \)和\( D\)，解得$$B=i \frac{\sin (2 l a)}{2 k l}\left(l^{2}-k^{2}\right) F$$ $$F=\frac{e^{-2 i k a} A}{\cos (2 l a)-i \frac{\left(k^{2}-l^{2}\right)}{2 k l} \sin (2 l a)}$$透射系数\( T=|F|^{2} /|A|^{2} \)的倒数可以表示为$$T^{-1}=1+\frac{V_{0}^{2}}{4 E\left(E+V_{0}\right)} \sin ^{2}\left(\frac{2 a}{\hbar} \sqrt{2 m\left(E+V_{0}\right)}\right)$$那么当\(\displaystyle\frac{2 a}{\hbar} \sqrt{2 m\left(E_{n}+V_{0}\right)}=n \pi\)全部透过，势阱变为完全透明，此时的总能量为$$E_{n}+V_{0}=\frac{n^{2} \pi^{2} \hbar^{2}}{2 m(2 a)^{2}}$$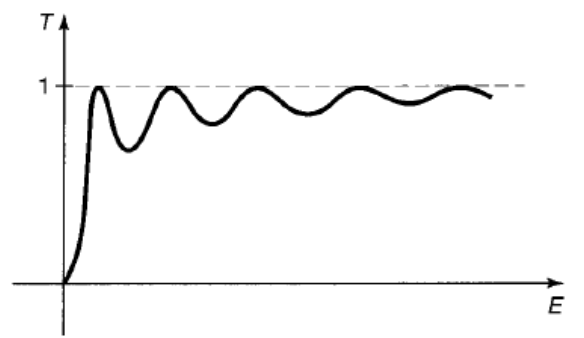
恰好是一维无限深势阱所允许的能量。其实此时势阱内波函数在边界概率正好为零，于是一个粒子过来，就好像没有看到这个势阱，直接穿透过去了。
上面讨论的是Finite potential well的情况，如果是一个rectangular barrier呢？同样地，如果是束缚态\( 0<E<V_{0} \)，那么$$T^{-1}=1+\frac{V_{0}^{2}}{4 E\left(V_{0}-E\right)} \sinh ^{2}\left(\frac{2 a}{\hbar} \sqrt{2 m\left(V_{0}-E\right)}\right)$$ 可以知道，当波长满足特定条件，可以完全穿透这个barrier，当然实际情况是不能完全穿透，但是或多或少有穿透一部分，这就是“量子隧穿效应”。
拓展：实际应用
(1) 量子阱(Quantum well)和量子阱红外探测器(QWIP)
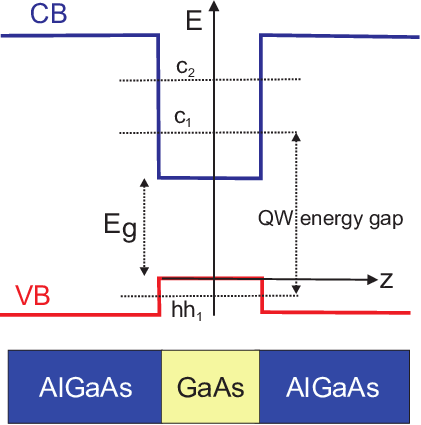利用分子束外延，长出这种结构，三个单质热源喷出来。图中其实就是Finite potential well。上面的槽(虚线)，对电子来说是well，下面的槽对空穴来说是well。对GaAs来说，室温下的禁带宽度为1.42 eV，三元的AlGaAs禁带宽度更大，取决于掺入Al的比例。可以通过调控GaAs的宽度(控制长晶体时间)以及AlGaAs中Al的比例来调控Finite potential well的状态。如果只是GaAs，那么我们探测到的发光波长对应于它的禁带宽度，但是如果是上图的这种量子阱结果，会有对应QW energy gap的电子和空穴的复合(叫作“band-to-band transition”)，可以通过探测复合产生的光子波长来对应到量子阱的状态。也就是说，通过控制QW energy gap，可以调控发光波长。
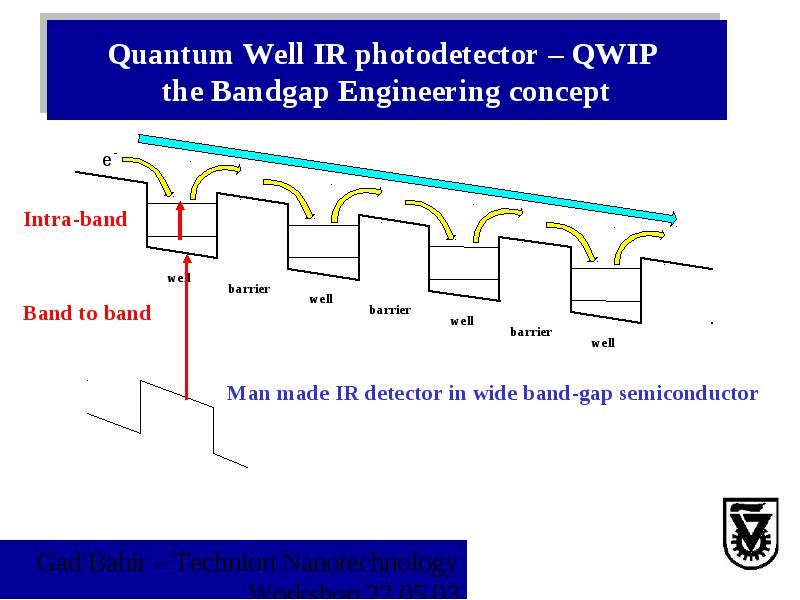电子吸收一个光子，但是到达的激发态能量不足以跑出QW，需要外加的bias(电场)助攻一下，就可以跑掉了，形成光电流，于是就测量到了光的信号。可实现QWIP imgaing来监测人体温度分布，虽然反应速度快，但是不太实用，主要问题是需要在液氮环境下工作。反应迅速，刷新率高，可以放在导弹上，灌好液氮，然后追着飞机跑，因为飞机是热源，发出红外线，被QWIP探测器探测到。
(2) 隧穿效应的应用
(3) 量子点？
xxx