Matrix Representations of Groups

The symmetry operations in a group may be represented by a set of transformation matrices \(\Gamma(g)\), one for each symmetry element \(g\) . Each individual matrix is called a representative of the corresponding symmetry operation, and the complete set of matrices is called a matrix representation of the group. The matrix representatives act on some chosen basis set of functions, and the actual matrices making up a given representation will depend on the basis that has been chosen. The representation is then said to span the chosen basis.

A matrix representation of a group obeys all of the rules set out in the formal mathematical definition of a group. 之前讲过群的定义，这里一样的。

Example: a matrix representation of the \( C_{3v}\) point group (the ammonia molecule)

The first thing we need to do before we can construct a matrix representation is to choose a basis. We selecte a basis \(\left(s_{N}, s_{1}, s_{2}, s_{3}\right)\) that consists of the valence s orbitals on the nitrogen and the three hydrogen atoms. 

The effects of the symmetry operations on our chosen basis are as follows:

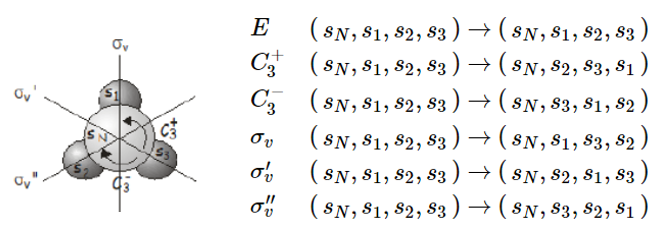
By inspection, the matrices that carry out the same transformations are:

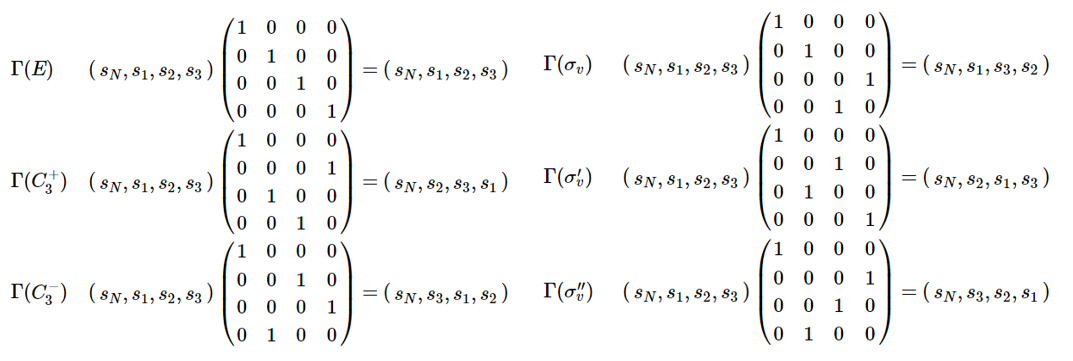
These six matrices therefore form a representation for the \(C_{3 v}\) point group in the \(  \left(s_{N}, s_{1}, s_{2}, s_{3}\right)\) basis. They multiply together according to the group multiplication table and satisfy all the requirements for a mathematical group.

注：这里写的都是row vector，如果写成column vector，那就是矩阵作用于向量(矩阵在左边)，相同对称操作的矩阵，row vector和column vector的对应的矩阵是互为转置(transposed)的。

Example: a matrix representation of the \( C_{2v}\) point group (the allyl radical)

In this example, we’ll take as our basis a \(p\) orbital on each carbon atom \(\left(p_{1}, p_{2}, p_{3}\right)\) . Note that the \(p\) orbitals are perpendicular to the plane of the carbon atoms (this may seem obvious, but if you’re visualizing the basis incorrectly it will shortly cause you a not inconsiderable amount of confusion). The symmetry operations in the \( C_{2v}\) point group, and their effect on the three \(p\) orbitals, are as follows:

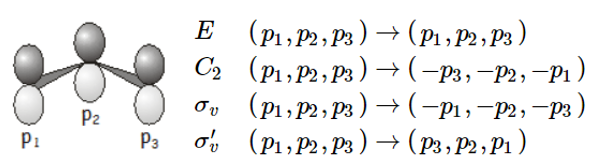
The matrices that carry out the transformation are
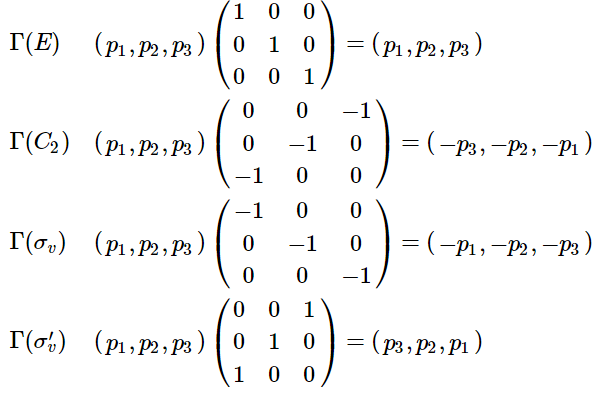Properties of Matrix Representations

Now that we’ve learnt how to create a matrix representation of a point group within a given basis, we will move on to look at some of the properties that make these representations so powerful in the treatment of molecular symmetry.

Similarity Transforms

A basis set \(\left(x_{1}, x_{2}, x_{3}, \ldots x_{n}\right)\).  The matrix representatives for the two basis sets will certainly be different, but we would expect them to be related to each other in some way (a similarity transform). 

Similarity Transforms is important when we use group theory to choose an optimal basis set with which to generate molecular orbitals.

由basis set \(\left(x_{1}, x_{2}, x_{3}, \ldots x_{n}\right)\) 线性组合得到新的basis set \(\left(x_{1}^{\prime}, x_{2}^{\prime}, x_{3}^{\prime}, \ldots x_{n}^{\prime}\right)\) $$\left(x_{1}^{\prime}, x_{2}^{\prime}, \ldots x_{n}^{\prime}\right)=\left(x_{1}, x_{2}, \ldots x_{n}\right)\left(\begin{array}{cccc} c_{11} & c_{12} & \ldots & c_{1 n} \\ c_{21} & c_{22} & \ldots & c_{2 n} \\ \ldots & \ldots & \ldots & \ldots \\ c_{n 1} & c_{n 2} & \ldots & c_{n n} \end{array}\right)$$

Now we look at what happens when we apply a symmetry operation g to our two basis sets. If \(\Gamma(g)\) and \(\Gamma^{\prime}(g)\) are matrix representatives of the symmetry operation in the \(\mathbf{x}\) and \(\mathbf{x}^{\prime} \) bases, then we have:
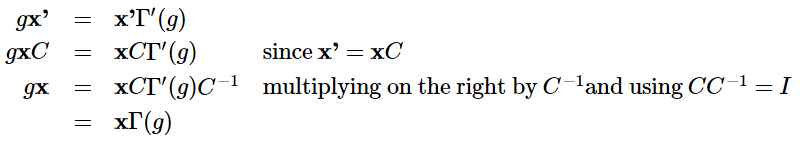We can therefore identify the similarity transform relating \(\Gamma(g)\) , the matrix representative in our original basis, to \(\Gamma^{\prime}(g)\) , the representative in the transformed basis. The transform depends only on the matrix of coefficients used to transform the basis functions. $$\Gamma(g)=C \Gamma^{\prime}(g) C^{-1} \quad\quad\Gamma^{\prime}(g)=C^{-1} \Gamma(g) C$$比如\( C_{3}^{+}\)和\( C_{3}^{-}\)就可以通过上述变换矩阵联系起来。

(1)操作所变换的对象，不仅可以是原子，或者空间一个点的位置，还可以是原子轨道或者分子轨道。
(2) 相似变换不会改变矩阵的迹。

Characters of Representations

The trace (迹) of a matrix representative \(\Gamma(g)\) is usually referred to as the character of the representation (表示的特征标) under the symmetry operation \(g\). $$\chi(g)=\sum_{i} \Gamma(g)_{i i}$$We will soon come to see that the characters of a matrix representation are often more useful than the matrix representatives themselves. Characters have several important properties.

• The character of a symmetry operation is invariant under a similarity transform
• Symmetry operations belonging to the same class have the same character in a given representation. Note that the character for a given class may be different in different representations, and that more than one class may have the same character.
• Two operations belong to the same class when one may be replaced by the other in a new coordinate system that is accessible by a symmetry operation.

Reduction of Representations I

对于\(C_{3v}\) representation, f we look at the matrices carefully we see that they all take the same block diagonal form (a square matrix is said to be block diagonal if all the elements are zero except for a set of submatrices lying along the diagonal).

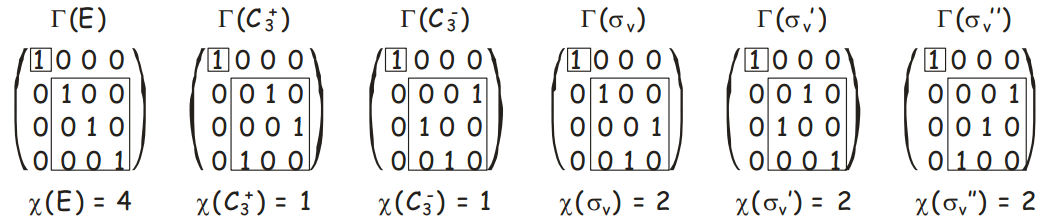A block diagonal matrix can be written as the direct sum of the matrices that lie along the diagonal. In the case of the \(C_{3v}\) matrix representation, each of the matrix representatives may be written as the direct sum of a \(1 \times 1\) matrix and a \(3\times 3\) matrix. $$\Gamma^{(4)}(g)=\Gamma^{(1)}(g) \otimes \Gamma^{(3)}(g)$$The reason why this result is useful in group theory is that the two sets of matrices \(\Gamma^{(1)}(g)\) and \(\Gamma^{(3)}(g)\) also satisfy all of the requirements for a matrix representation. 每个set都有identity元素，每个元素的逆元素都在set里面，等等群的一些性质。回忆一下the basis for the original four-dimensional representation had the \(s\) orbitals \(\left(s_{N}, s_{1}, s_{2}, s_{3}\right)\) of ammonia as its basis. The first set of reduced matrices, \( \Gamma^{(1)}(g) \), forms a one-dimensional representation with \(\left(s_{N}\right)\) as its basis. The second set, \(\Gamma^{(3)}(g) \) forms a three-dimensional representation with the basis \(\left(s_{1}, s_{2}, s_{3}\right)\). Separation of the original representation into representations of lower dimensionality is called reduction of the representation. The two reduced representations are shown below.

(1) The \(1\times 1\) representation in which all of the elements are equal to \(1\) is sometimes called the unfaithful representation, since it satisfies the group properties in a fairly trivial way without telling us much about the symmetry properties of the group.
(2) 从群的高维表示得到(多个)低维(共同)表示的过程,称为表示的约化(reduction of the representation)

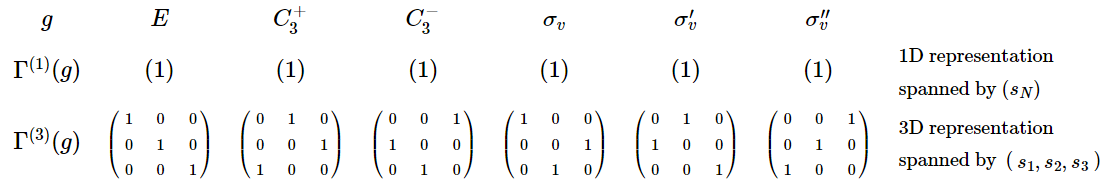
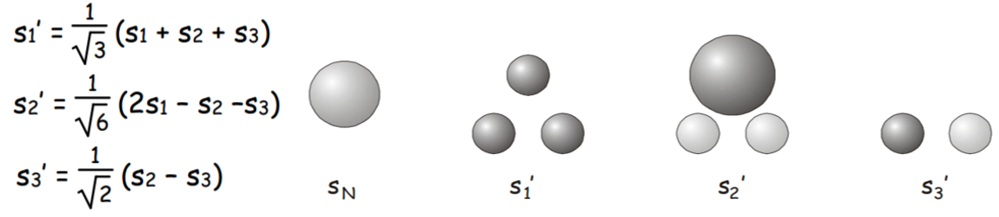
The logical next step is to investigate whether or not the three dimensional representation \( \Gamma^{(3)}(g)\) can be reduced any further. As it stands, the matrices making up this representation are not in block diagonal form (老师说了\(E\)和\(\sigma_{v}\)are block diagonal，但是应该\( \sigma_{v}^{\prime}\)也是啊，只是和前面两个划分block的方式不同，not in the same block diagonal form), so the representation is not reducible. However, we can carry out a similarity transformation to a new representation spanned by a new set of basis functions (made up of linear combinations of \(\left(s_{1}, s_{2}, s_{3}\right)\)), which is reducible. In this case, the appropriate (normalized) linear combinations to use as our new basis functions are
or in matrix form
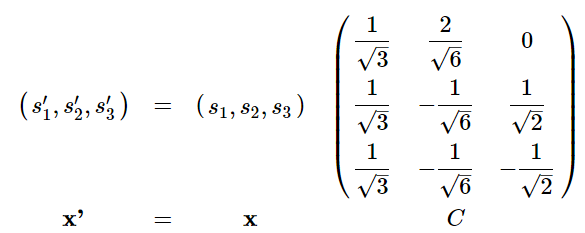The matrices in the new representation are found from \( \Gamma^{\prime}(g)=C^{-1} \Gamma(g) C\) to be

We see that each matrix is now in block diagonal form, and the representation may be reduced into the direct sum of a \(1 \times 1 \) representation spanned by \(  \left(s_{1}^{\prime}\right)\) and a \(2 \times 2\) representation spanned by \(\left(s_{2}^{\prime}, s_{3}^{\prime}\right)\). The complete set of reduced representations obtained from the original 4D representation is:
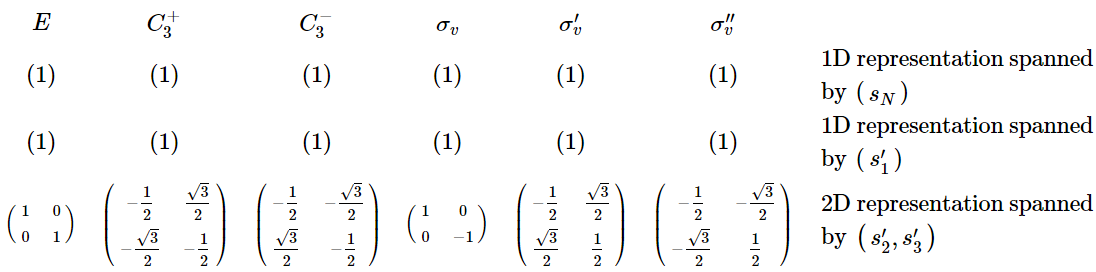This is as far as we can go in reducing this representation. None of the three representations above can be reduced any further, and they are therefore called irreducible representations (不可约表示), or ‘irreps’, of the point group.

Formally, a representation is an irreducible representation if there is no similarity transform that can simultaneously convert all of the representatives into block diagonal form.

The linear combination of basis functions that converts a matrix representation into block diagonal form, allowing reduction of the representation, is called a symmetry adapted linear combination (SALC) 对称适应线性组合.

Irreducible representations and symmetry species

The two one-dimensional irreducible representations spanned by \(s_{N}\) and \(s_{1}^{\prime}\) are seen to be identical (见上一节图片). This means that \(s_{N}\) and \(s_{1}^{\prime}\) have the ‘same symmetry’, transforming in the same way under all of the symmetry operations of the point group and forming bases for the same matrix representation. As such, they are said to belong to the same symmetry species. There are a limited number of ways in which an arbitrary function can transform under the symmetry operations of a group, giving rise to a limited number of symmetry species (任何函数只有有限多个symmetry species). Any function that forms a basis for a matrix representation of a group must transform as one of the symmetry species of the group. The irreducible representations of a point group are labeled according to their symmetry species as follows:

• 一阶的矩阵表示：1D representations are labeled \(A\) or \(B\) , depending on whether they are symmetric (character \(+1\)) or antisymmetric (character \(-1\)) under rotation about the principal axis.
• 二阶的矩阵表示：2D representations are labeled \(E\)
• 三阶的矩阵表示：3D representations are labeled \(T\) (或者 \(F\)).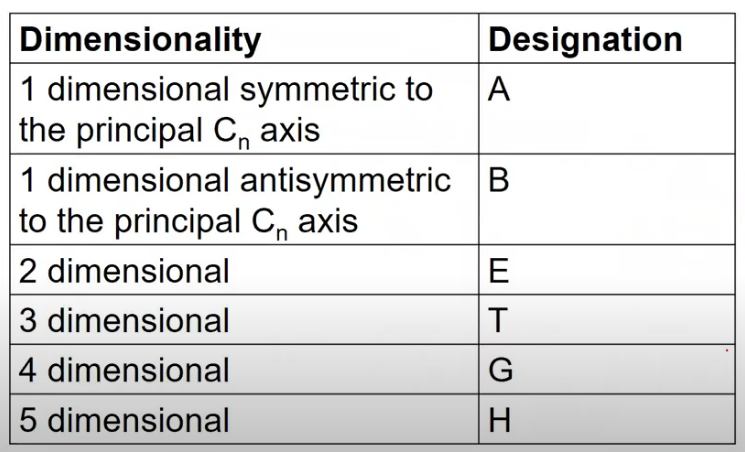以上这些叫作Mulliken符号，常用在讨论量子化学有关问题及分子原子光谱学时。 另外，还有Bethe符号:Γ1， Γ2， Γ3……以及其他符号。 Bethe符号常用于固体光谱。 不同领域采用不同的符号，只是习惯 问题，并没有什么特殊的道理，但是却造成了复杂的符号系统。
• In groups containing a center of inversion, \(g\) and \(u\) labels (from the German gerade and ungerade, meaning symmetric and antisymmetric) denote the character of the irreducible representation under inversion ( \(+1\) for \(g\), \(-1\) for \(u\))
• In groups with a horizontal mirror plane but no center of inversion, the irreducible representations are given prime \(^{\prime}\) and double prime \(^{\prime \prime}\) labels to denote whether they are symmetric (character \(+1\) or antisymmetric (character \(-1\)) under reflection in the plane.
• If further distinction between irreducible representations is required, subscripts \( 1\) and \( 2\) are used to denote the character with respect to a \( C_2\) rotation perpendicular to the principal axis, or with respect to a vertical reflection if there are no  rotations.
  

The 1D irreducible representation in the \( C_{3v}\) point group is symmetric (has character \(+1\)) under all the symmetry operations of the group. It therefore belongs to the irreducible representation \( A_{1}\). The 2D irreducible representation has character \( 2\) under the identity operation, \(-1\) under rotation, and \( 0\) under reflection, and belongs to the irreducible representation \( E\).

Sometimes there is confusion over the relationship between a function \( f\) and its irreducible representation, but it is quite important that you understand the connection. There are several different ways of stating the relationship. For example, the following statements all mean the same thing:

• \( f\) has \(A_2\) symmetry
• \( f\) transforms as \(A_2\)
• \( f\) has the same symmetry as \(A_2\)
• \( f\) forms a basis for the \(A_2\) irrep

The most important point to understand is that every function transforms as one of the irreps of a point group. In the case of one-dimensional irreps there is a one-to-one correspondence between the function and its irrep. In the case of two-dimensional irreps, a pair of degenerate functions will transform jointly as the 2D irrep, and so on. The same function may transform as a different irrep in different point groups. For example, a \( p_z\) orbital on an atom in a tetrahedral environment (e.g. a \( p_z\) orbital on the C atom in CH₄) transforms as \( T_2\) (along with the two other p orbitals), while a \( p_z\) orbital lying along the rotation axis of a \( C_{3v}\) molecule (such as the \( p_z\) orbital on the N atom in NH₃) transforms as \(A_1\).

Character Tables

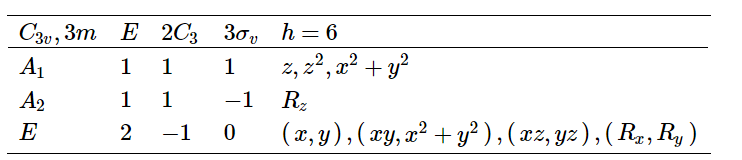
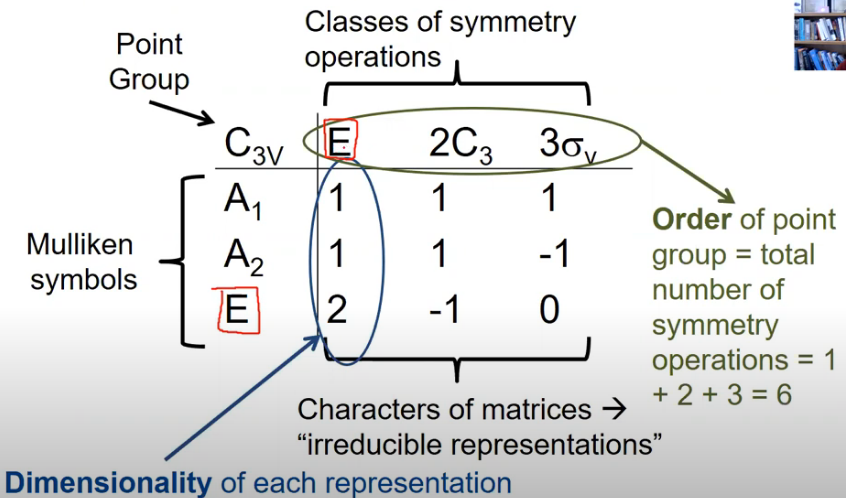
说明(第一张图)

• The first element in the table gives the name of the point group, usually in both Schoenflies (\( C_3v\) ) and Hermann-Mauguin ( \(3m\) ) notation.
• The characters of the irreducible representations under each symmetry operation are given in the bulk of the table.
• The final column of the table lists a number of functions that transform as the various irreducible representations of the group. These are the Cartesian axes \((x, y, z)\), the Cartesian products \(\left(z^{2}, x^{2}+y^{2}, x y, y z\right)\), and the rotations \(\left(R_{x}, R_{y}, R_{z}\right)\).
  这一列非常重要(特别是对光谱学而言)。For example, by looking at the transformation properties of \(x\), \(y\) and \(z\)(sometimes given in character tables as \(T_x\), \(T_y\), \(T_z\)) we can discover the symmetry of translations along the \(x\) , \(y\), and \(z\) axes. Similarly, \(T_x\), \(T_y\) and \(T_z\) represent rotations about the three Cartesian axes. As we shall see later, the transformation properties of \(x\), \(y\) and \(z\) can also be used to determine whether or not a molecule can absorb a photon of \( x -\), \( y-\), or \(z -\) polarized light and undergo a spectroscopic transition. The Cartesian products play a similar role in determining selection rules for Raman transitions, which involve two photons.

 

 

 

Four Rules of Character Tables

(1) The sum of squares of the dimensionalities of the irreducible representations of a group is equal to the order of the group (=total number of symmetry operations).
对于上面的例子，就是第一列(对应dimensionality)的数据平方和：$$1^{2}+1^{2}+2^{2}=1+2+3=6$$(2) In any irreducible representation, the sum of squares of each character multiplied by the number of operations in that class is equal to the order of the group. $$\begin{aligned} &A_1:1\left(1^{2}\right)+2\left(1^{2}\right)+3\left(1^{2}\right)=1+2+3 \\ &A_2:1\left(1^{2}\right)+2\left(1^{2}\right)+3(-1)^{2}=1+2+3 \\ &E:1\left(2^{2}\right)+2(-1)^{2}+3\left(0^{2}\right)=1+2+3 \end{aligned}$$(3) The vectors of two different irreducible representations whose components are the characters multiplied by the number of operations in that class are orthogonal. $$\begin{aligned} &A_{1} \cdot A_{2}=1(1) 1+2(1)(1)+3(1)(-1)=0 \\ &A_{1} \cdot E=1(1) 2+2(1)(-1)+3(1)(0)=0 \\ &A_{2} \cdot E=1(1) 2+2(1)(-1)+3(-1)(0)=0 \end{aligned}$$(4) The number of irreducible representations and the number of classes in a group are equal.
这里左侧第一列(除了左上角第一个元素)对应的的是不可约表示(3个)，而第一列也有3类对称操作，这两个数值上相等也保证了character table永远有square matrix shape (不考虑最后一页)。每一列就是一个不可约表示的vector。

Reduction of reducible representations into irreducible representations (将可约表示写成不可约表示线性组合的形式)  $$a_{m}=\frac{1}{h} \Sigma_{g} \chi(g) \chi_{m}(g)$$其中
(1) \(a_{m}\)是is the number of times the irreducible representation occurs in the reducible representation. (不可约表示前面组合系数)
(2) \(\chi(g)\)是要被分解的可约特征标表示
(3) \(\chi_{m}(g)\)是第\( m^{\text {th }}\)个不可约表示
(4) \(h\) is the order of the group

We can of course write this as a sum over classes rather than a sum over symmetry operations. $$a_{m}=\frac{1}{h} \Sigma_{C} n_{C} \chi(g) \chi_{m}(g)$$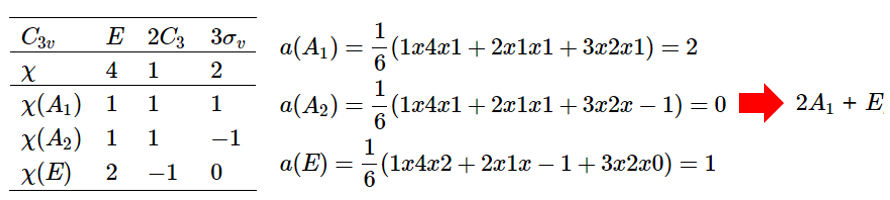

分析\(D_{6h}\)点群的特征标表

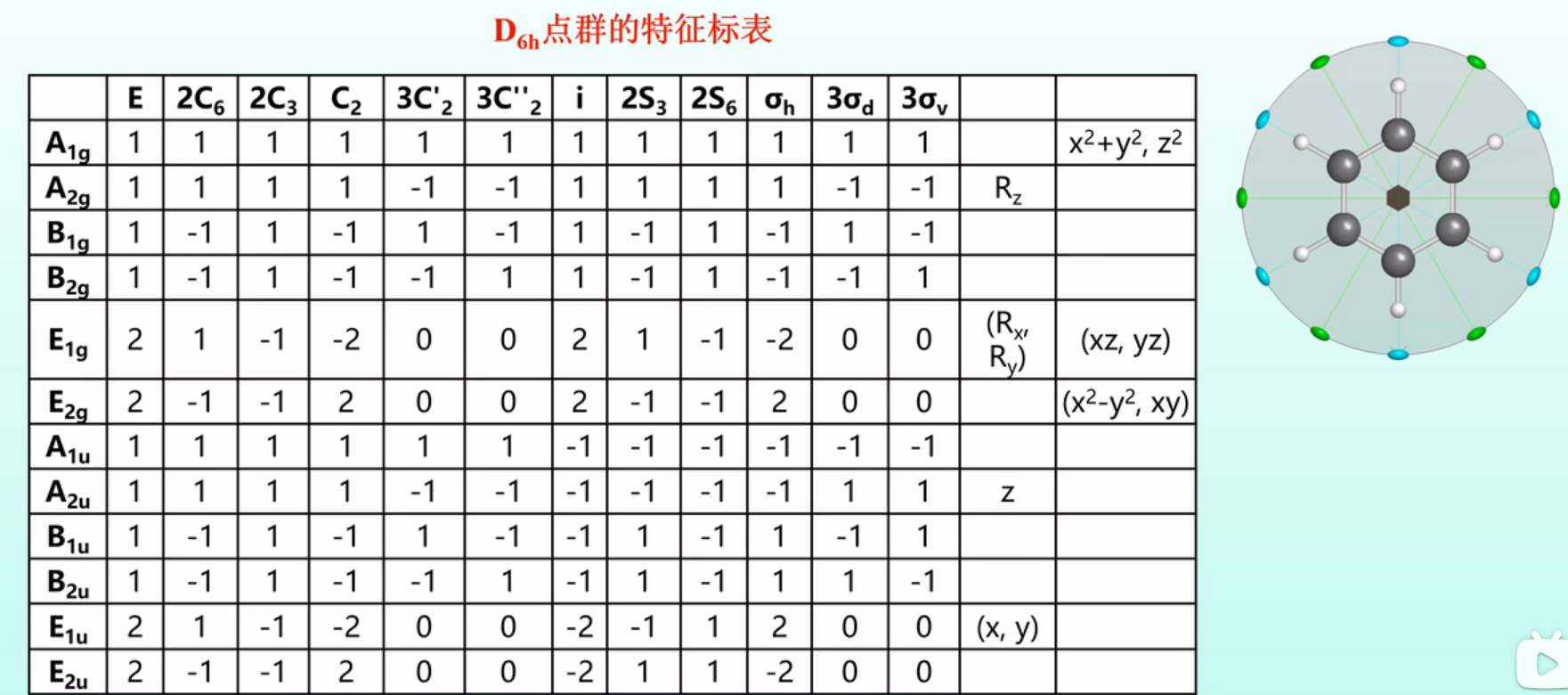
• 第3/4/5列都对应着\(C_6\)操作，只是有时候等价于其他旋转操作，所以实际上第3列的2\(C_6\)说的是\(C^{1}_6\)和\(C^{5}_6\)，而第4列\(2C_3  \)说的是\(C^{2}_6\)和\(C^{4}_6\)，第5列\(C_2\)说的是\(C^{3}_6\)。
• 第6列的\(3C^{\prime}_2\)说的是图中蓝色的对称轴。
• 第7列的\(3C^{\prime\prime}_2\)说的是图中绿色的对称轴。
• 对于\(S^{n}_3 \)存在多个操作，但是有些操作和其他对称操作重复了，所以真正独立的操作只有\(S^{1}_3 \)和\(S^{5}_3 \)，将它们归类到一起，写成了\(2S_3 \)。
  比如\(S^{2}_3 \)转240度，反演两次，相当于只转一次240度，\(S^{3}_3 \)相当于\(\sigma_{h}\)操作。
• 对于\(S^{n}_6 \)也类似，只有\(S^{1}_6\)和\(S^{5}_6\)是独立操作。
• 第一列的A和B都是一维的，所以其\(E\)这一栏下，都是1；\(E\)在\(E\)这一栏下就是2。
• A和主轴对称，B和主轴反对称，看\(C_6\)操作这一栏，分别对应1和-1。
• 看下表，垂直于主轴的\(C_2\)轴对称的写1，反对称的写2，这里我们看第6列，下标1对应1，下标2对应-2。
• 对于\(i\)对称中心，正数(1或2)说明是对称的，下标就是g，负数(-1或-2)则下标是u。